桩土阻尼作用下低应变法可测桩长的分析
张献民,曹宗亮
(中国民航大学机场学院,天津 300300)
低应变反射法是在桩身完整性检测中应用最为普遍的一种动力检测方法。由于其分析理论和实践应用都较为成熟,操作方法简便,分析结果直观,从而被大多数检测人员广泛地应用在桩基检测领域[1]。
然而,应力波在桩身传递过程中由于能量的衰减,从而使低应变检测方法在对长度较大的基桩进行完整性检测时受到一定限制。本文利用一维波动理论,建立桩土相互作用的方程,得到了波幅比与桩身长度呈一定的反比关系,并通过计算得到低应变检测的可测桩长范围。通过Ansys Ls-Dyna进行模拟,验证了计算分析的正确性。
1 可测桩长的计算分析
本文的研究对象为长度较大的灌注桩,作为摩擦桩处理,忽略桩底土作用。为了便于分析,忽略桩身材料的阻尼作用,同时,对低应变条件下桩土相互作用系统做如下假设:桩视为一维弹性直杆,在桩侧土均匀的条件下,桩周土对桩的作用简化为开尔文力学模型,即土对桩的作用用一个线性弹簧和线性阻尼器并联的方式共同作用,其中分布弹簧刚度系数为ks,分布阻尼系数为ηs。而桩身应力波的衰减几乎不受桩侧土刚度的影响[2],因此,忽略桩土刚度比的影响,而只考虑桩侧土的阻尼作用。
假设桩长为L,在桩顶施加的脉冲力为p(t),其对应的定解问题如下
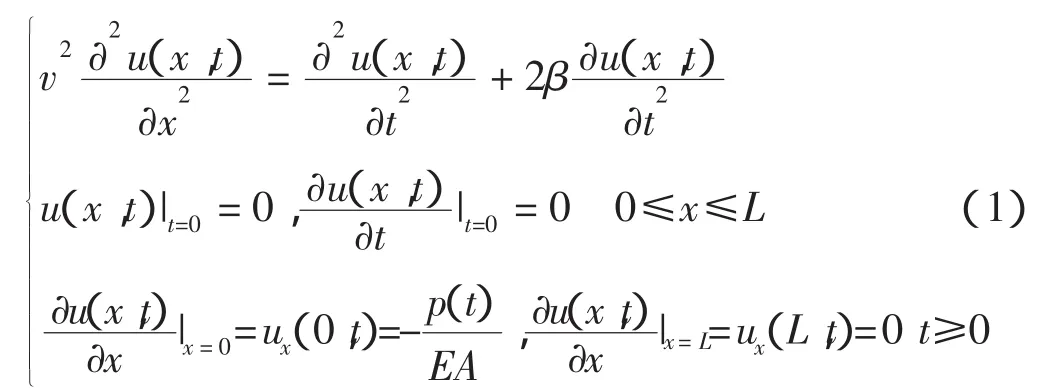
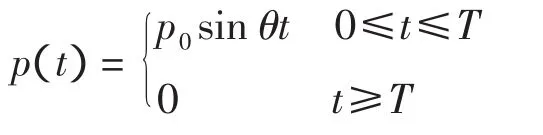
式中:T为脉冲宽度。
1.1 桩土阻尼系数与波幅比的关系
在桩侧土为均质土的条件下,得到的摩擦桩桩顶接收到的反射波波幅与初始入射波波幅的比值与桩侧土阻尼系数及时间满足如下关系[3]
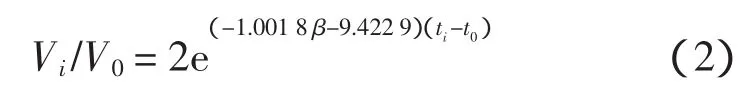
式中:t0为与桩顶入射波波幅V0对应的时间(s);ti为与桩顶接受第i次反射波波幅Vi对应的时间,i=1,2,3...。
由式(2)可得,接受到第一次桩底反射时,桩顶接受的入射波幅与接受到的桩底反射波幅之比与阻尼系数的关系为
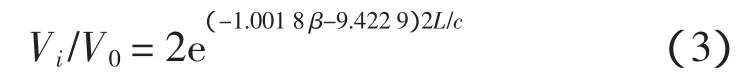
式中:L 为桩身长度(m);c为应力波波速(m/s),根据混凝土灌注桩的强度可以确定。
1.2 桩土阻尼系数与桩身长度的关系
阻尼系数受土质条件和饱和状态对的影响,同时与桩侧土的上覆有效压力有如式(4)所表示的关系,相同应力条件下砂土的阻尼系数最小,粉土次之,黏土最大[4]

式中:σ 为桩侧土的上覆有效应力(kPa);C1、C2的取值如表1所示。

表 1 C1、C2的取值Tab.1 Value of C1、C2
1.3 波幅比与桩长的关系
在均质土中某深度的有效应力为
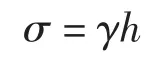
一般桩的埋设深度h约等于桩身长度L,为简化计算,整桩深度内的等效应力为

将式(4)、式(5)带入式(3)中有
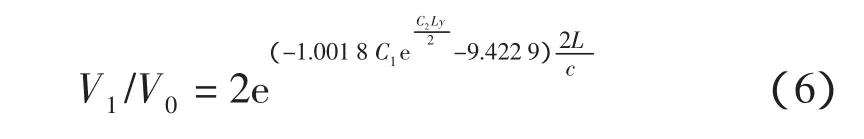
由此可以得出,桩底反射波的波幅与桩顶初始入射波波幅的比值与桩周土的性质、桩身长度及桩身波速有关。
1.4 临界桩长的计算分析
取阻尼系数最小的天然砂土和阻尼系数最大的饱和软黏土,重度均取为19 kN/m3,工程中灌注桩混凝土强度等级一般在C20~C40,波速范围为3 400~4 500 m/s,此处设砂土中的桩身波速为4 500 m/s,黏土中的桩身波速为3 400 m/s。Rending认为V1/V0=1/10 000是检测范围的下限[4],则将以上数值带入式(6)中有:
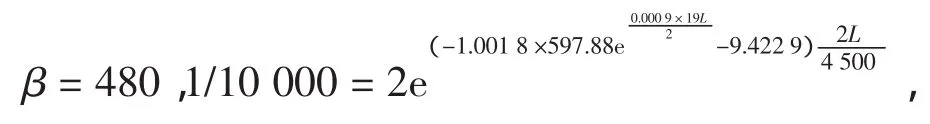

通过阻尼系数最小的天然砂土和阻尼系数最大的饱和软黏土的计算分析,可以看出对于低应变法,要采集到清晰的桩底反射,其可能的最大桩长范围介于31~45 m之间。
2 有限元模拟分析
通过Ansys Ls-Dyna对低应变条件下的桩土做如下模拟[5-6]:
桩身长度分别选取以上讨论的不同土质条件下可测桩长临界值,即45 m和31 m,桩截面为圆形,半径r=1.0 m,桩身中的波速取同于以上的计算模型,分别为4 500 m/s和3 400 m/s,则相应弹性模量取为E=4.65×1010N/m2,E=2.66×1010N/m2,二者的桩身密度均取为ρ=2300kg/m3,泊松均比μ=0.2,忽略配筋。在桩的周围设桩周土,厚度为3.0 m。取桩周土弹性模量E=1 × 1018N/m2,密度 ρ= 1 900 kg/m3,泊松比 μ =0.3。桩和土的单元类型均为SOLID164。
在本文中桩身的单元尺寸为0.2 m,为了节省时间将桩周土的尺寸划的稍大一些,划为0.5 m,均采用映射网格划分。网格划分后的模型如图1所示。常规振源为一瞬态锤击脉冲信号,力幅度A和脉冲宽度T(时间)为衡量它的主要指标。本文的激振力模型采用半正弦波函数近似描述。

在用有限元进行无限边界地基系统的分析时,往往需要用一个无限域来表示土体。为了限制模型的规模,同时又要防止用有限域表示时从边界反射回来的反射波对系统的影响,本文使用DYNA中定义的非反射边界条件来表示用有限域代表无限域时采用的模型边界。
为考虑桩土阻尼对应力波衰减的影响,Dyna中是通过EDDAMP命令施加阻尼作用来减小结构中的振动。通过对长度20 m的模拟桩,分别施加200、250、300、350、400、450、500、550、600 的阻尼,通过模拟得出波幅比,将波幅比代入式(6)中,可以算得其与桩土间的阻尼系数的对应关系如表2所示。

表2 桩土阻尼系数的等效阻尼的确定Tab.2 Equivalent damping of pile-soil damping
通过对相关数据拟合得到阻尼系数和Dyna中的阻尼存在如下关系
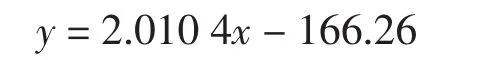
其拟合情况如图2所示。
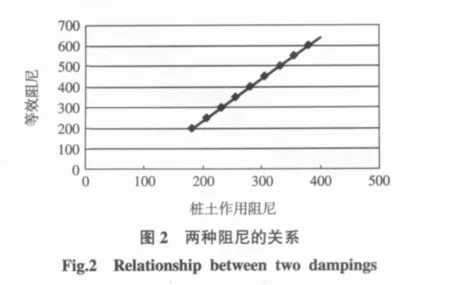
将以上讨论的天然砂土的阻尼系数和饱和软黏土的阻尼系数代入上式,可以分别得到Dyna中的阻尼为800和920,考虑桩土阻尼作用下的天然砂土和饱和软黏土条件下桩顶质点的速度时程曲线如图3和图4所示。
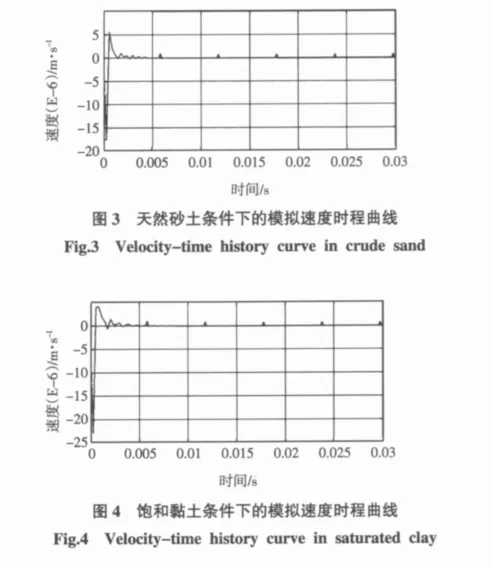
由于桩土阻尼的作用,图中很难清晰地看到接收到的桩底反射,但是通过对计算所得数据的分析可以看到:
1)图3中,在距离入射波峰△t=0.020 1 s时刻有桩底反射波峰。在图4中,在距入射波峰△t=0.018 6 s时刻有桩底反射,反射波与入射波同相,符合摩擦桩的波形特点,根据其对应波速,计算得出L1=45.2 m、L2=31.6 m,符合有限元模型设计值及模型计算值。
2)图3中,反射波波幅为1.7×10-9m/s,而桩顶入射波幅为1.76×10-5m/s,计算可得波幅比V1/V0=0.000 097,恰好达到Rending提出的1/10 000的可测范围的下限,由此,得以验证45 m为天然砂土中可测的临界桩长。
3)图4中,反射波波幅为2.1×10-9m/s,而桩顶入射波幅为2.29×10-5m/s,计算可得波幅比V1/V0=0.000 092,恰好达到Rending提出的1/10 000的可测范围的下限,由此,得以验证31 m为饱和软黏土中可测的临界桩长。
由有限元模拟分析与模型计算分析可以看出,低应变法可测桩长的范围一般不超过45 m,超过这个范围,将很难测到桩底反射波形,从而影响对桩身质量的判断。
3 结语
本文在计算分析和模拟分析的基础上得到了如下结论:
1)通过建立摩擦桩的桩土相互作用模型,分析了桩土作用阻尼对应力波能量衰减的作用,通过计算分析,得到了在不同土质下低应变反射波法采集清晰桩底反射的桩长界限,即均质天然砂土下低应变可测桩长不超过45 m,饱和软黏土不超过31 m,这也是成层土中可测桩长范围值。
2)通过桩土阻尼系数和Ls-Dyna阻尼的对比分析,给出了二者之间的关系。
3)通过Ansys Ls-Dyna三维有限元分析,对模型计算得到的临界桩长进行了模拟分析,验证了计算的正确性。
本文的研究内容对于低应变反射波法在桩基检测领域的研究具有一定的借鉴意义,该研究结果在长桩检测领域的进一步研究有一定的参考价值。本文的研究模型较为简单,忽略了一些相关因素的影响,期待进一步的完善研究。
[1] 刘兴录.桩基工程与动测技术200问[M].北京:中国建筑工业出版社,2000:52-53.
[2] 蔡 靖,王建华,张献民.桩基完整性检测中桩身应力波衰减规律及其应用[J].水文地质工程地质,2005,32(5):73-76.
[3]智胜英,王建华.测定低应变桩土相互作用阻尼系数的试验方法.[J].水文地质工程地质,2008,35(6):85-89.
[4] RENDING F J.A new Generation of Foundation Pile Diagostic Equtpment[C]//Proc of the Third International Conference on the Application of Stress-wave Theory to Piles.Ottavoa,1988.
[5] 赵振东,山本三千雄,铃木善雄伟.桩基低应变完整性检测的分析研究[J].地震工程与工程振动,1995,15(4):104-111.
[6] 季勇志,王元战.基于ANSYS LS-DYNA的码头基桩完整性检测的数值模拟和方法研究[J].振动与冲击,2010,29(2):199-201.

