液氧贮箱增压过程中气枕空间温度场的数值模拟
尚存存 耑 锐 王 文
(上海交通大学制冷与低温工程研究所 上海 200240)
符号表
α:体积分数
t:时间,s
v:速度,m/s
ρ:密度,kg/m3
S:源项
u:X方向速度分量,m/s
v:Y方向速度分量,m/s
w:Z方向速度分量,m/s
p:压力
h:比焓,kJ/kg
η:动力粘度,kg/(m·s)
T:温度,K
λ:流体的导热系数,kJ/(m·K)
q:热流密度,kJ/(m2·s)
δ:有效界面膜厚度,mm
CA:组元A的摩尔浓度,kmol/m3
CA0:组元A的初始浓度,kmol/m3
D:扩散系数,m2/s
θ:扩散时间,s
M:相对分子质量
σ:平均碰撞直径
Ω:分子扩散碰撞积分
N:摩尔通量,kmol/(m2·s)
cpA:平均比定压热容,kJ/(kg·K)
α:对流传热系数,kJ/(m2·K)
i:单位质量的焓,kJ/kg
y:气相的摩尔分数
P:贮箱总压力,×101.325 kPa
下标
l:液相
A:气氧
o:高温氧气
v:气相
B:液氧
w:壁面
1 引言
高温氧气进入低温液氧储箱的自生增压方式是液氧贮箱增压气体输送的一种重要形式,在这一过程中,由于气枕温升以及气体流动,相界面附近液体会出现温升,并且会影响到低温液氧的热与流动特性。研究增压气体输送过程中气枕温度以及流场,可以确定液氧温度变化,分析蒸发与沸腾现象。这对于液氧的稳定输送以及发动机的安全工作非常重要。
目前,国内外已经有与低温贮箱的气枕空间温度、压力及流场相关的研究。Lawrence[1]建立了二维非平衡态双区域数学模型,研究了低温推进剂贮箱内因外部环境漏热造成的自然对流及热分层的起因及发展,并分析了气枕初始条件、填充率及增压对热分层的影响。Stephen J Mattick[2]等提出可以用于推进剂贮箱及主推进系统组件的计算方法,讨论了3种不同的贮箱增压方式的应用,预测了贮箱温度及其压力的变化并进行对比分析。程向华[3-5]等采用CFD技术对带有预冷回路的液氧贮箱内部的物理场进行数值模拟,分析了液氧热分层的形成过程及原因,得出回流口截面以上区域传热以对流方式为主,而底部区域以导热方式为主;对不同气枕压力下液氢贮箱内部的物理场进行数值模拟,分析了气枕压力对贮箱内不同部位处液氢温度及热边界层厚度、边界层速度的影响。
基于国内外关于低温贮箱中增压输送过程中气枕空间的研究主要为二维计算模型,且集中为气枕初始条件及其压力的研究。本文以增压气体输送过程中的液氧贮箱为研究对象,采用三维非稳态模型。基于双膜阻理论建立热质交换模型,模拟分析气枕空间在增压气体输送过程中的温度场的变化及其对于贮箱内低温液氧的影响,为低温液体燃料贮箱结构的优化设计提供重要的理论依据。
2 模型的建立
2.1 物理模型
贮箱由圆柱筒体及上下两个椭圆形封头组成,贮箱顶部开有氧排气阀,安全阀和增压口。贮箱外包有一定厚度的保温材料,如图1所示。以直径为3.35 m的贮箱模型为研究对象,考虑到模拟的贮箱顶部结构非对称,采用三维非稳态模型,根据贮箱结构特点,对其网格进行分区划分并且局部加密,气枕空间为可压缩理想气体。设置8个特征点Z1—Z8,如图2所示。
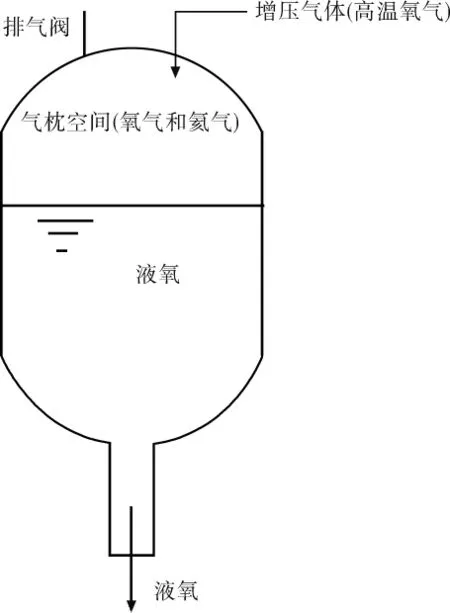
图1 液氧增压系统示意图Fig.1 Schematic diagram of liquid oxygen pressurization system
2.2 控制方程
对于贮箱内部流场,其控制方程可以写成如下形式[6]:
质量守恒方程:
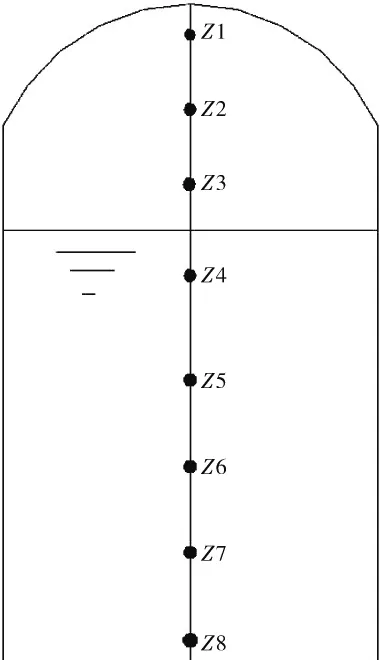
图2 特征点Z1—Z8的位置Fig.2 Location of point Z1-Z8
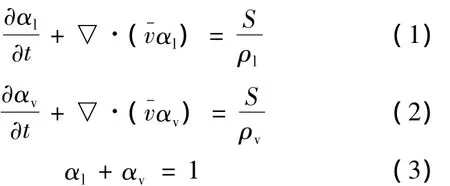
动量守恒方程:
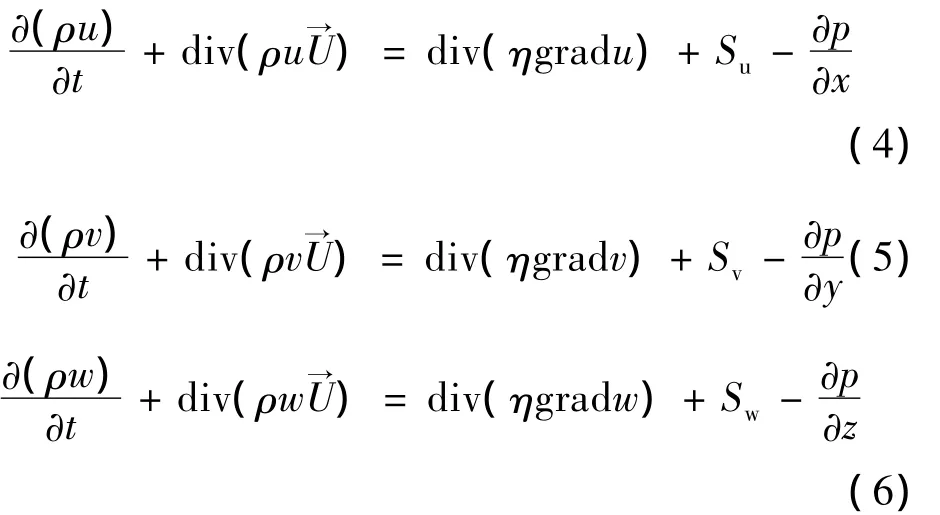
能量守恒方程:
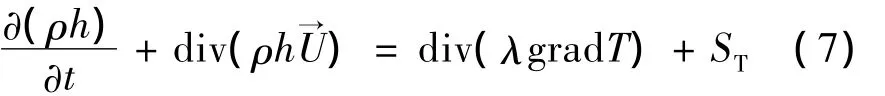
其中,低温液氧下降过程中,气液相界面的传热作为源项耦合到能量守恒方程中。
2.3 初始及边界条件
边界条件见表1,在计算过程中,外部环境温度为15℃,不考虑风速的影响。贮箱气枕空间的温度按顶点的230 K计算,贮箱内液体的初始温度按90.1 K 计算。

表1 计算边界条件Table 1 Parameters of computational boundary
2.4 依据双膜阻理论建立热质交换层模型
对于液氧贮箱内的自由相界面采用VOF模型,对于液氧贮箱中的低温相变问题,依据双膜阻理论建立热质交换模型,解决液氧贮箱中的相变和因相变产生的热质交换问题。
两相平衡是分析相际传质的重要条件,而两相化学势相等是两相平衡的条件。双膜阻理论为:一组元由甲相到乙相的传质过程为,首先在甲相中由主体传递至相界面,然后跨过相界面到达乙相主体中。
δ是有效界面膜厚度,由式(8)决定:
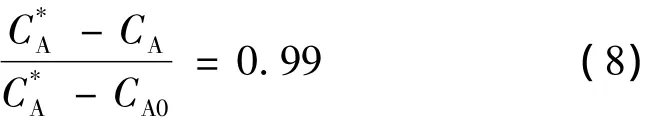
但是得出δ的精确解比较困难,所以拟用:

作为溶质在界面膜中不稳定传质的近似方程时的浓度分布来求解。
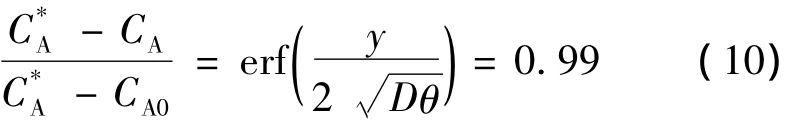
[7]中的式(11)、式(12):
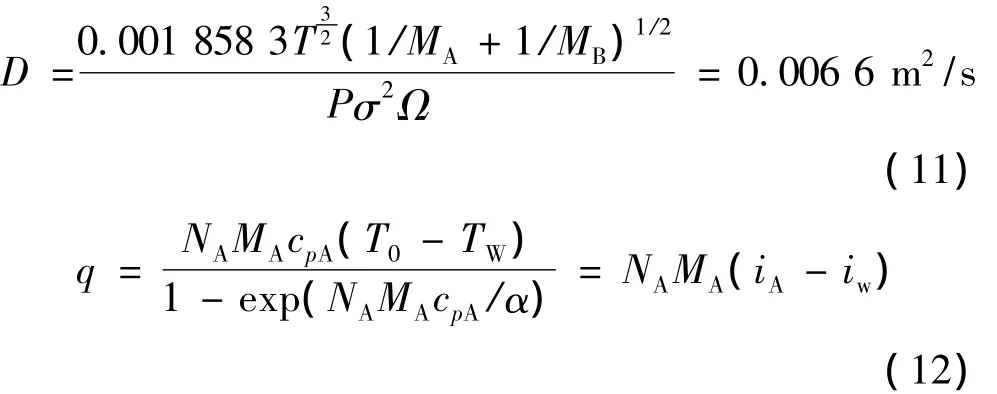
传热传质膜层中,每个计算单元内,内能的不平衡(动能和焓的不平衡)是传热传质的动力。
3 计算结果与分析
增压气体为高温氧气,随着高温增压气体进入液氧贮箱,其顶部的气枕空间的温度受到较大的扰动,图3为在液氧贮箱增压过程中,气枕空间3个特征点的温度随时间的变化情况。
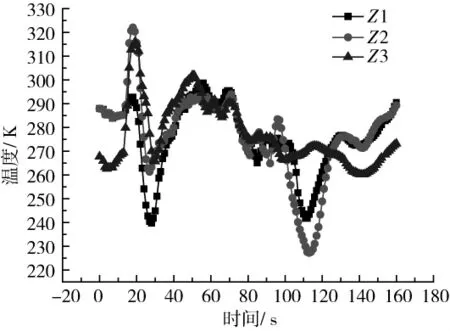
图3 特征点Z1、Z2、Z3的温度随时间的变化Fig.3 Temperature variation of point Z1-Z3 with time
从图3特征点Z1、Z2和Z3的温度随时间的变化中可以看到,随着高温增压气体流入贮箱,特征点Z1、Z2和Z3的温度逐渐升高。由于高温增压气体的射流以及涡旋气流的卷吸夹带,相界面附近的低温气体沿壁面流入顶部空间,因而顶部温度在22 s没有升高反而下降到最低值,之后迅速回升。从约60 s开始,Z1、Z2和Z3的温度总体呈现下降趋势,有一定的波动。这和气枕空间的平均温度值的变化趋势基本上一致。
气枕空间的平均温度随时间的变化情况如图4所示,可以看出,随着高温增压气体的流入,气枕空间的质量加权平均温度在短暂的上升至280 K左右后,随着液氧的流出,气枕空间逐渐增大,贮箱内低温液氧不断的蒸发,因此,低温氧气逐渐增多,气枕空间的质量加权平均温度迅速下降,而后随着高温气体的流入,气枕空间的质量加权平均温度略有升高,在70 s时,气枕空间质量加权平均温度出现小幅度的下降,之后基本趋于稳定。
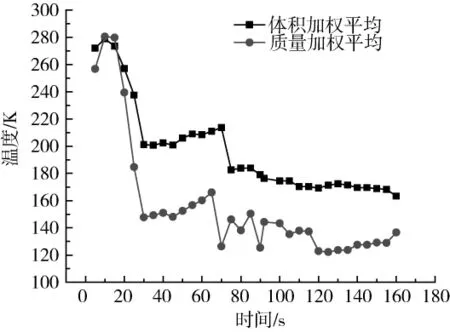
图4 气枕空间的平均温度随时间的变化图Fig.4 Average temperature variation of ullage with time
为了进行比较,同时求出了气枕空间的体积加权平均温度。可以看出,其变化趋势和质量加权平均温度基本一致,体积加权平均温度值高于质量加权平均值,这是因为氧气的密度大于相同状态下氦气的密度;由于气体的密度波动较大,质量加权平均温度波动幅度稍大于体积加权平均的波动幅度。
图5为贮箱中心线上5个特征点的温度随时间的变化情况,可以看出,随着贮箱内液面的下降,贮箱下部特征点的温度波动幅度大于上部特征点的波动,这就表明随着液氧的排出,气枕空间逐渐增大,其内部的涡旋逐渐下移,对贮箱上部的扰动较小,气枕空间纵向也会出现较为明显的温度分层现象。
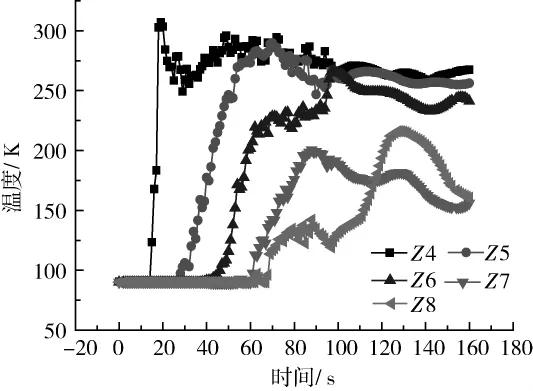
图5 贮箱中心线上特征点的温度随时间的变化Fig.5 Center line points temperature variation with time
气枕空间在特定的时刻 10 s、30 s、70 s、130 s 时的温度场分布如图6所示,可以看出,随着低温液体的排出,气枕空间出现较为明显的温度分层,高温气体的向下扩散速度远远低于低温液体液面的下降速度,相界面的热质交换主要在液氧和低温气氧间进行,高温增压气体主要分布于气枕的上部空间,这对于贮箱内液氧的稳定是有利的。
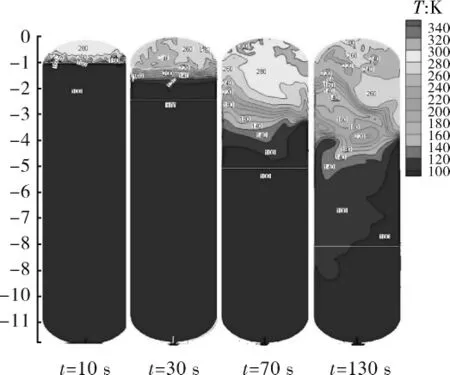
图6 X=0截面上贮箱内部温度场(白色直线上部即为相应的气枕空间)Fig.6 Temperature field of X=0 section within tank(Ullage is above the white straight line)
贮箱内的压力场的分布如图7所示,可以看出随着高温增压气体流入低温贮箱,气枕空间形成一定的压力梯度,且其顶部的压力大于液氧表面的压力值。这是因为,增压气体输送过程中,高温增压气体向下的扩散速度远低于液氧液面的下降速度,并且低温液氧的蒸发量不足以使得气枕空间下部区域的压力场和其顶部持平。可以得出液氧表面在10 s、30 s、70 s 及 130 s 时 的 压 力 分 别 为0.3 MPa、0.335 MPa、0.285 MPa、0.31 MPa。由液氧的物性参数可知,标准大气压下,液氧的沸点分别为90 K,而由图6可以得出,10 s时液氧表面约为150 K,相应的饱和压力为4.218 6 MPa,远远高于此状态下液氧表面的压力值,液氧表面出现了沸腾现象;30 s、70 s及130 s时液氧表面的温度均为90 K,表面压力远大于标准大气压,因此,此时液氧表面不会出现沸腾现象。
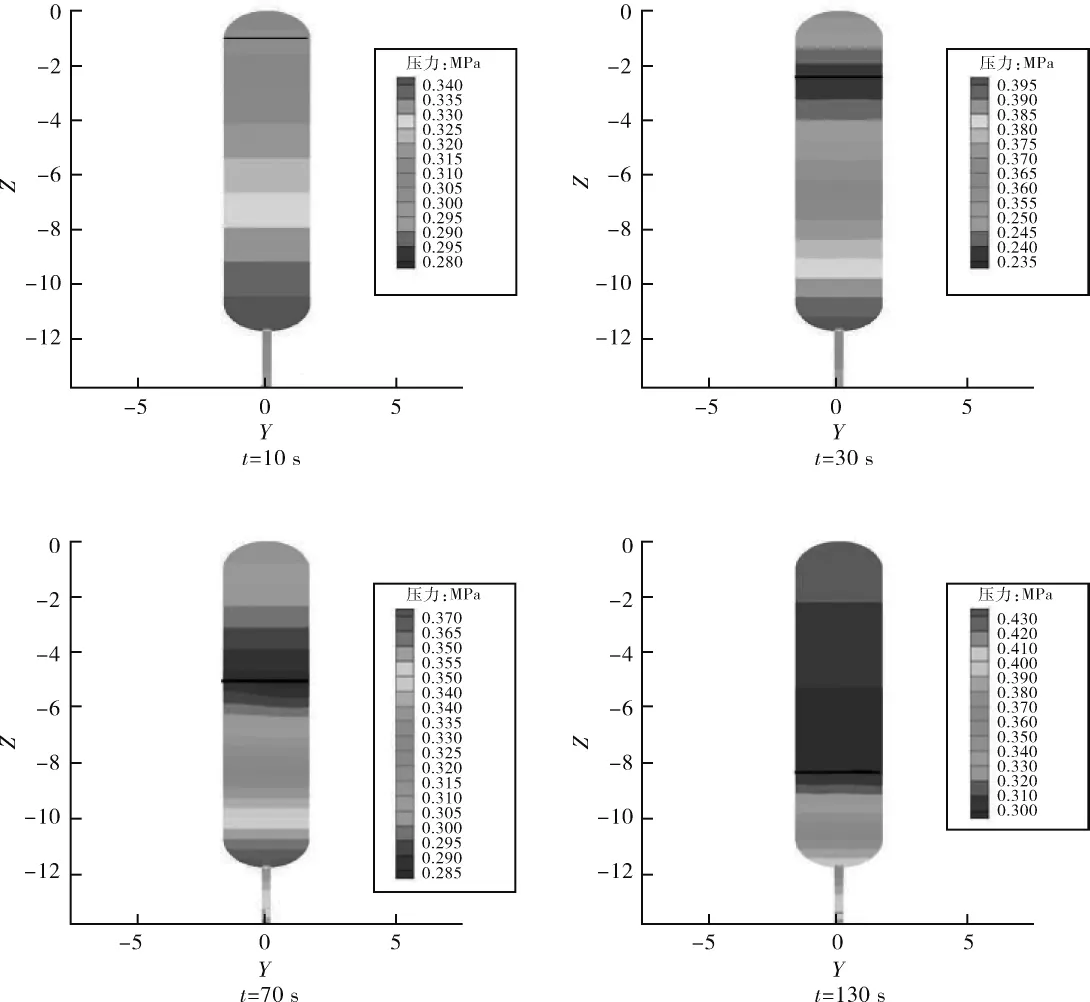
图7 X=0截面上贮箱内部压力场(黑色直线为气液相界面)Fig.7 Pressure field of X=0 section within tank(Black straight line represents interface)
4 结论
通过模拟贮箱内非稳态热流过程,得出了气枕空间在增压气体输送过程中温度场的变化及其对于贮箱内低温液氧的影响情况。
(1)增压气体输送过程中,气枕空间受高温增压气体射流和涡旋气流的卷吸作用,会出现温度的暂时骤降,之后温度逐步提高,气枕空间顶部的温度趋于均匀。
(2)随着高温增压气体的流入和液氧的流出,气枕空间出现明显的温度分层,气枕空间的平均温度在短暂的上升至280 K左右后迅速下降,之后稳中有小的波动。其体积加权平均温度高于相应的质量加权平均温度值,且其温度波动幅度小于质量加权平均温度的波动。
(3)增压气体输送过程中,气枕空间的体积逐渐增大,其内部的涡旋逐渐下移,高温气体向下的扩散速度远远低于液氧液面的下降速度,利于贮箱内液氧的稳定。
(4)增压气体输送过程中,初始阶段液氧表面会出现沸腾现象,之后随着液氧液位的下移,液氧表面不再出现沸腾现象。
参考文献
1 Lawrence M.A numerical study of thermal stratification due to transient natural convection in densified liquid propellant tanks[D].New Orleans,USA,University of New Orleans,2003.
2 Stephen J Mattick,Chun P Lee.Progress in modeling pressurization in propellant tanks[C].Joint Propulsion Conference&Exhibit,Nashville,2010.
3 程向华,厉彦忠,陈二峰.火箭液氧贮箱热分层现象数值模拟[J].低温工程,2008(2):10-13.
4 程向华,厉彦忠,陈二峰,等.新型运载火箭射前预冷液氧贮箱热分层的数值研究[J].西安交通大学学报,2008(9):1132-1136.
5 王 磊,厉彦忠,程向华.气枕压力对液氢热分层的影响规律[J].低温工程,2009(6):18-22.
6 陶文铨.数值传热学[M].西安:西安交通大学出版社,2002.
7 王补宣.工程传热传质学[M].北京:科学出版社,1982.

