改进的机载阵列调频连续波合成孔径雷达前视成像方法

侯海平 曲长文 杨 俭 苏 峰

（1.91039部队，北京102401；2.海军航空工程学院电子信息工程系，山东 烟台264001）

1.引 言

20世纪90年代，德国宇航局（DLR）的 Witte提出基于阵列技术的前视合成孔径雷达（SAR）来改善常规SAR机底盲区等问题［1］。典型的前视成像雷达系统是用于视景增强的新型区域成像雷达（SIREV），它由 DLR 高频技术研究所和德国Karlsruhe大学等合作研发。文献［2］－［4］根据SIREV原理研究了基于Extended Chirp Scaling（ECS）算法的前视成像，文献［5］借鉴了ScanSAR将数据补零至全孔径的方法，完善了ECS算法，文献［6］结合距离多普勒（RD）算法研究了SAR前视三维成像。

目前，阵列SAR前视成像研究涉及的问题主要体现在：（1）研究的信号体制主要是脉冲SAR，且ECS算法不适用于处理调频连续波（FMCW）SAR通过De－chirp方式得到的回波数据。作为新的成像体制，FMCW SAR具有体积小、成本低、结构紧凑等优势［7－9］，适合于机载平台。对于距离向 Dechirp数据，通常采用频率变标（FS）［10－11］和 Chirp－Z变换实现距离向的变标。文献［8］提出一种针对FMCW体制基于二维Chirp－Z变换变标的成像算法。但FS算法的运算量较Chirp－Z变换小得多，且通过引入比例因子可以解决FS算法在波束较宽时变标函数的模糊问题［9］。（2）研究的信号模型认为载机速度可以忽略，但实际上除了载机悬停状态，应考虑载机运动的距离差对阵列天线接收信号相位的影响，不能按照载机速度可忽略的情况来处理，这就需要重新进行信号建模。

针对上述问题，本文根据FMCW体制的特点，在信号模型中考虑了载机速度参数，研究了改进的机载阵列FMCW SAR前视成像方法，并结合性能参数通过成像仿真对本文方法进行了分析验证。

2.信号建模

前视SAR天线由阵元彼此相邻且独立的接收天线阵和一个独立的相参发射天线组成。定义载机运动方向为航线向，垂直于机身布置线性阵列的方向为跨航向。根据SAR原理，接收天线阵通过数据采集与相参处理生成等效的合成孔径，获得跨航向高分辨率。将雷达接收天线对回波依次接收一遍后的时间视为等效的相干积累周期Ts，回波数据经过跨航向和径向距离向聚焦后可以得到单幅前视SAR图像［6］。天线切换频率与扫频频率是一致的，切换速度vs满足［2］

式中：d为相邻接收阵元间距；Tr为扫频周期。

根据FMCW SAR的信号特性，研究“等效双基的单阵元发射多阵元顺序接收”模式。P点坐标为Ptar＝ （x0，y0），α为波束入射角，如图1所示。在Ts时间内，考虑信号收发时载机的运动，发射天线到点目标的瞬时斜距RT为

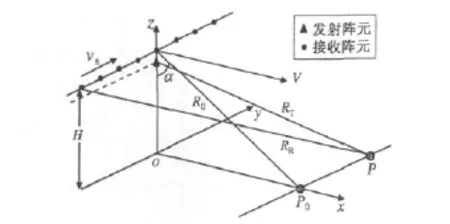
图1 SAR前视成像几何示意图

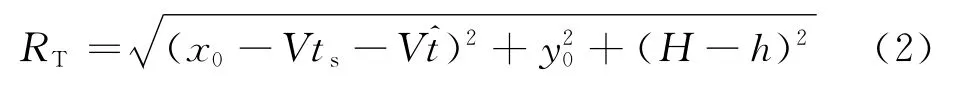
式中：H为载机高度；V为载机速度；ts为阵元切换的慢时间；为发射信号的快时间；h为接收天线中心到正下方发射天线的距离。

点目标到第n个接收阵元的瞬时斜距RR，n为

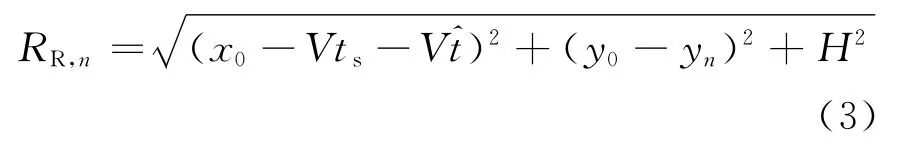
式中，yn为第n个接收阵元的y轴坐标。

由于接收阵元以速度vs切换，因此将跨航向位置yn表示为切换速度vs与时间变量ts的形式，有

在式（2）和（3）中，令

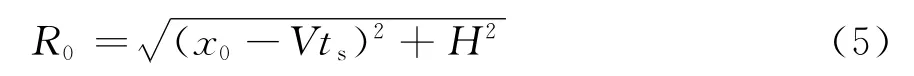
将RT和RR，n在处作泰勒展开并忽略高阶项有

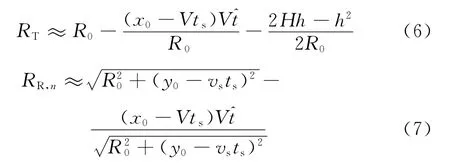
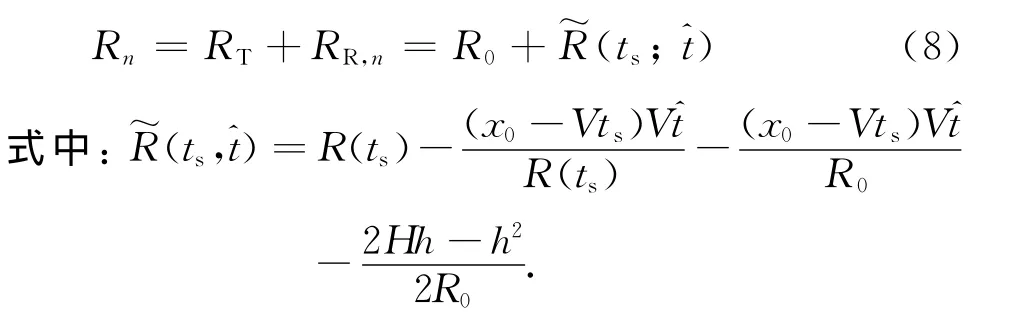
3.信号特性分析

3.1 载机速度的影响

通常认为前视SAR载机速度很小，在接收阵元切换时间内可以忽略载机速度的影响［5］，但该近似处理会对成像带来不利的影响。

一方面，载机速度对脉冲SAR和FMCW SAR的影响都不能忽略。目标到阵元的距离与载机速度相关，在相干积累周期Ts内，阵元位置随载机速度的变化如图2所示。圆点表示载机悬停状态时接收阵元的位置，方点和星点分别表示载机作低速和高速运动且速度不能忽略时接收阵元的位置，此时需要考虑在信号接收过程中载机速度对成像产生的影响。

图2 载机运动对瞬时斜距的影响

另一方面，载机速度对脉冲SAR和FMCW SAR的影响又不完全相同，该差别受信号占空比制约，体现在信号接收过程中载机连续运动的影响。对于常规脉冲SAR，通常认为“停－走”假设成立［12］。同样，对于前视脉冲SAR，阵元切换接收回波可以按“停－走”模式处理，只需考虑两阵元切换时间的载机位移即可。对于前视FMCW SAR，由于整个扫频周期都发射信号，接收机始终处于接收状态，需要考虑两阵元切换过程中载机连续运动的影响。

当信号模型中不考虑载机速度，即令V＝0时，RR，n表示为Rn0，则式（8）可表示为

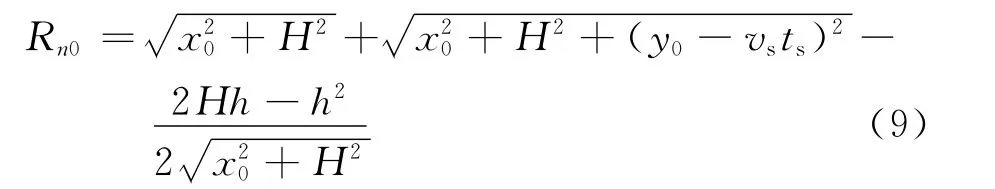
考虑载机速度V之后，与载机悬停状态相比，引入的路程差为

为了保证成像聚焦，要求双程运动误差所引起的相位误差变化最大不能超过π／4rad，即

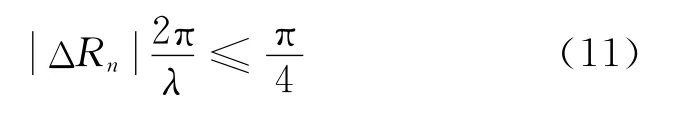
式中，λ为入射波波长。

根据式（10）和式（11）求出载机速度V 的范围为

考虑ΔRn最小的情况，即两阵元切换的间隔时间，此时可得

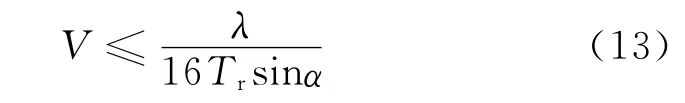
考虑ΔRn最大的情况，即经过一个相干积累周期，此时可得

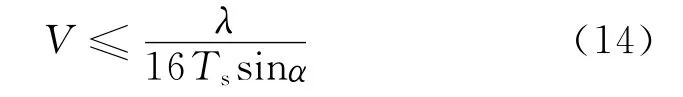
由式（13）和式（14）可见，近似处理后，制约载机速度的参数包括入射波波长λ、扫频周期Tr、阵元数N（Ts由N和Tr共同决定）以及波束入射角α.

在式（14）中，当N一定而Tr增大，或当Tr一定而N增大时，由于Ts时间内相位差增大，此时要求V变小；较小的λ以及较大的α同样限制了V.

3.2 跨航向多普勒特性

式（8）对ts求导得到多普勒频率为

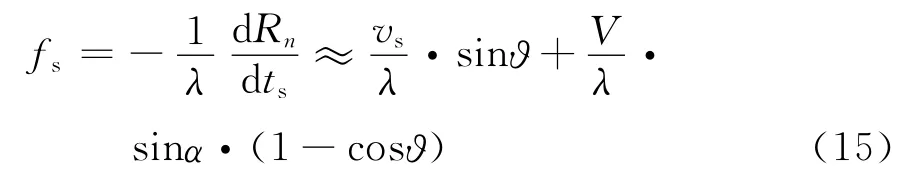
式中：ϑ为“点目标－接收阵元”连线与该连线在xoz平面内投影的夹角。

由式（15）可知，考虑载机运动后，多普勒频率是由载机速度和阵元切换速度在“点目标－接收阵元”径向距离方向的分量共同作用产生。

多普勒调频率为

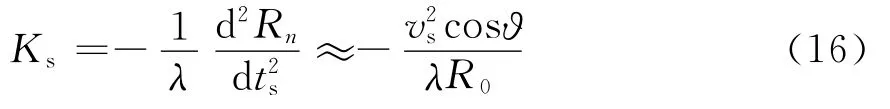
则相干积累周期Ts内的多普勒带宽Δfs为

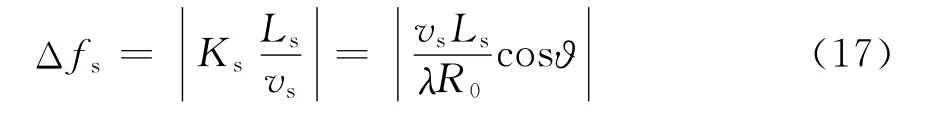
根据Δfs，求得跨航向分辨率ρs为

由式（18）可知跨航向分辨率随点目标位置变化。以接收阵元位于阵列中心为例，位于航迹线地面投影的点目标ϑ＝0，分辨率最高。当目标位于测绘区域两侧边沿时，ϑ最大，跨航向分辨率最低。

3.3 多普勒频率偏移

对于FMCW SAR，由载机连续运动引入的多普勒频率偏移可以通过式（8）对快时间t＾求导得到，即

式中：V·sinα为载机速度在数据录取平面内的径向速度分量。

分析式（19）可知，前视FMCW SAR由载机连续运动产生的多普勒频率偏移表现为以下几个特征：

1）多普勒频率偏移随α变化显著，在载机运动平面内，即α＝90°时，目标的多普勒频率偏移最大，α＝0°时为下视模式，多普勒频率偏移为零。

2）载机速度不变时，多普勒频率偏移与跨航向分辨单元相对于接收阵列的位置有关，目标与接收阵元在跨航向的相对距离越大，cosϑ越小，多普勒频率偏移越小。

3）位于航迹地面投影且处于波束中心的点目标，即图1中的P0点，其相对于接收阵元是对称的，因此，在接收阵元切换过程中，该点目标的多普勒频率偏移变化最小，由于接收阵列长度远小于地面场景宽度，其多普勒频率偏移近似为fd0，表示为

根据上述分析，对于前视FMCW SAR，载机运动产生的多普勒频率偏移比常规FMCW SAR复杂。多普勒频率偏移会引起回波包络的徙动，从而影响目标的聚焦。为了精确实现前视成像，在改进的方法中将对该影响进行补偿。而由式（19）可知，多普勒频率偏移随α和点目标位置变化的复杂性使得精确的多普勒频率偏移校正是不可能的，根据特征Ⅲ，在实际处理时选取P0点作为参考点近似处理。

4.成像算法

FS算法不需插值，仅通过块处理完成距离徙动校正，且只有复乘和快速傅里叶变换（FFT）运算，因此精度和运算效率很高［10－11］。由于FS算法引入了变标因子，波束较宽或有一定斜视角时，会引入一个信号带宽，当其大于FMCW雷达系统采样频率时，由于变标函数本身存在模糊而导致FS算法失效［8］。前视SAR波束覆盖区域很大，为了避免变标函数的模糊问题，对剩余视频相位（RVP）进行放大μ 倍处理［9］。

前视成像雷达可以看成一种特殊的ScanSAR，成像处理前首先借鉴ScanSAR的处理方法对前视成像数据采取两端补零操作。因为考虑了载机连续运动引入的多普勒频率偏移，改进的成像方法需要首先进行多普勒频率偏移补偿。

对于本文研究的信号收发模式，接收阵元以速度vs切换形成等效孔径，而发射路程除了对载机连续运动引入的多普勒频率偏移产生影响，对跨航向分辨率没有贡献［5］，因此后续信号处理中，以RR，n取代Rn，参考信号采用发射信号的延迟（τref＝2Rc／c）.不考虑信号幅度的影响，yn处接收阵元的混频信号表示为

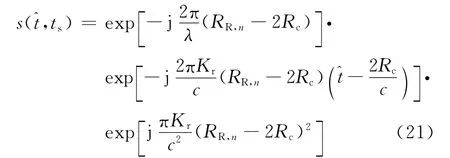
式中：Rc为场景中心P0对应的斜距；Kr为调频斜率；c为光速。第一个指数项为跨航向的相位历程，第二个指数项为径向距离信号，第三个指数项为RVP项，是FMCW SAR De－chirp处理特有的，会影响到跨航向的聚焦处理。

根据式（7）、（19）和（20），考虑载机连续运动时引入的距离差，距离历程可以表示为

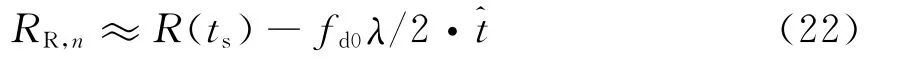
则式（21）为

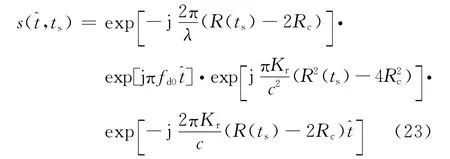
为了实现聚焦，需要对载机运动引入的多普勒频率偏移进行补偿，补偿函数为

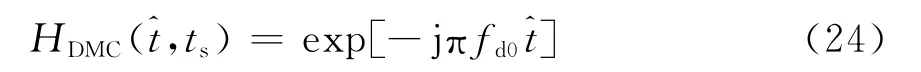
将补偿后的信号作径向距离向FFT，由于FMCW SAR中RVP的影响非常小，因此将RVP相位值增大μ倍后作变量代换并化简。作径向距离向逆快速傅里叶变换（IFFT）得［10］

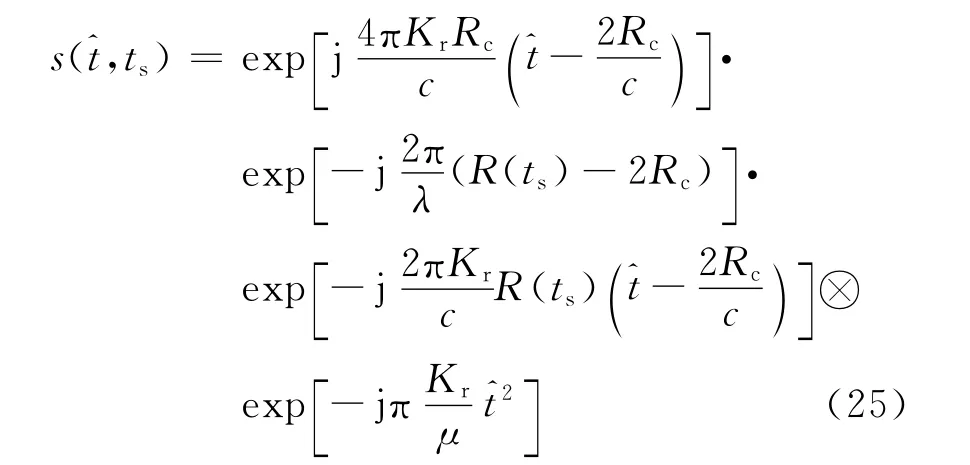
式中⊗表示卷积。

改进方法中后续的处理步骤，包括频率变标、RVP校正、逆频率变标、二次距离压缩（SRC）校正以及距离徙动校正等同常规FS算法相同，在此不作详细推导，可参考文献［10］。由于在改进FS算法中对RVP项进行了放大μ倍处理，因此算法中几个因子也需要相应地放大或缩小μ倍，主要包括以下几项：

频率变标项

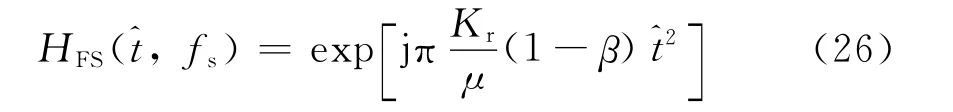
RVP校正项

逆频率变标项

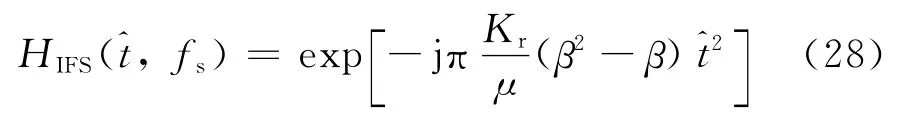
经过多普勒频率偏移补偿和二维聚焦处理后可以得到压缩信号为

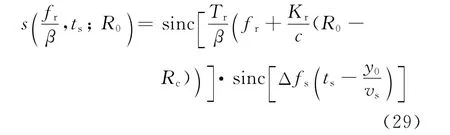
5.仿真分析

根据上述算法进行仿真分析，参数如表1所示。需要说明的是，为了有针对性地讨论载机运动和接收阵元数的影响，对载机速度和阵元数分别选取三组典型值，在仿真中会对实际选用的参数说明。

表1 仿真参数

首先对多点目标进行成像仿真，点目标坐标如表2所示，仿真选取阵元数为101。

表2 点目标位置

多点目标成像结果如图3所示。从图3可以看出，采用本文算法可以很好地实现分布多点目标的成像。后续仿真中结合具体的目标成像性能参数对单点目标成像效果分析。

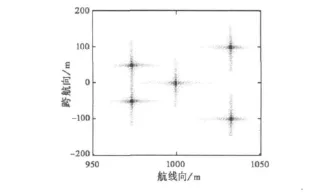
图3 多点目标成像结果

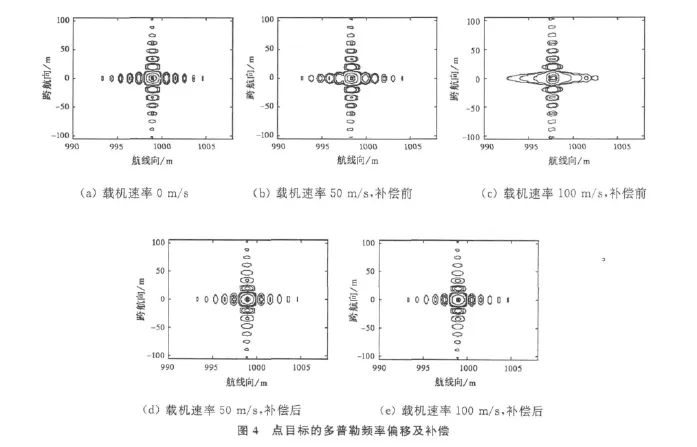
载机速度是本文信号模型和成像算法考虑的重要参数。为了分析载机连续运动产生的多普勒频率偏移，给出不同载机速度条件下的成像结果及补偿效果。设接收阵元数为1 0 1，载机速度分别为0m／s、50m／s和100m／s，对点目标P0进行仿真。图4（a）是载机速度为0m／s的结果，图4（b）和（c）为多普勒频率偏移补偿前的结果，图4（d）和（e）为补偿后的结果。

由图2已知，载机以一定的速度运动时，在接收天线切换的相干积累周期Ts内，接收阵元的位置是变化的。这种积累效应使得点目标位置在航线向发生了搬移，点目标像在航线向的坐标比实际位置的坐标要小。同时，载机连续运动产生的多普勒频率偏移主要引起了航线向主瓣变宽和旁瓣发生畸变，峰值旁瓣比（PSLR）和积分旁瓣比（ISLR）变差。由图4（d）和（e）可以看出，通过补偿后，点目标成像结果理想。

前视SAR在系统结构上区别于常规SAR的显著特点就是采用了阵列技术。前视阵列SAR跨航向分辨率与阵列长度有关，在阵元间距一定的条件下，接收阵元数越多，空间采样点数越多，跨航向分辨率越高，但同时信号处理数据量变大，系统更为复杂，因此需要兼顾信号处理的性能以及所需分辨率的要求对阵元数折中选取［14］。为了比较阵元数对跨航向分辨率的影响，设载机速度为0m／s，分别计算阵元数为101、151和201三种条件下点目标P4的性能参数，同时将不同载机速度条件下P0点的性能参数列于表3。综合以上仿真，可以得到如下结论：

1）在相参积累周期Ts内，随着载机速度的增大，接收阵元较理想位置的偏移量增大，成像点目标的航线向位置发生搬移（坐标变小）。

2）载机连续运动引入的多普勒频率偏移与载机速度有关。载机速度增大，多普勒频率偏移也增大，并且航线向主瓣变宽、旁瓣出现了畸变，PSLR、ISLR和分辨率变差，多普勒频率偏移可以通过补偿来消除。因此，前视成像需要根据实际应用在信号模型中考虑载机速度，并在算法实现时通过补偿消除它对成像的影响。

3）阵元间距为一定值时，阵元数的增加使得跨航向阵列的有效孔径长度增大，空间采样点数增多，从而有效提高了跨航向分辨率。跨航向分辨率的提高同时弱化了点目标在跨航向旁瓣的倾斜效应。

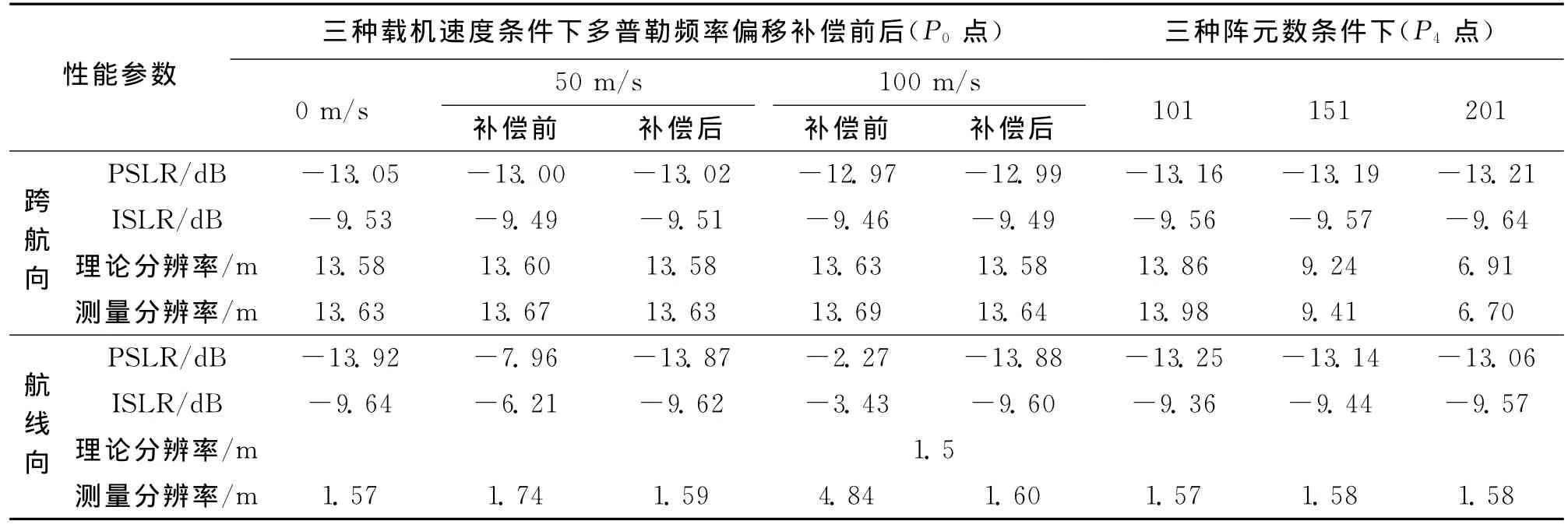
表3 点目标性能

6.结 论

本文给出了一种改进的机载阵列FMCW SAR前视成像方法，不仅在前视信号模型中将载机速度作为重要的参数进行考虑，而且给出了多普勒频率偏移的补偿方法。该方法有效解决了载机运动条件下的阵列FMCW SAR前视成像问题，仿真和数据分析结果很好地验证了本文算法的正确性和有效性。

［1］WITTE F.Forward looking airborne radar in combination with downward and side looking sensors［C］／／IEEE Comb Optical－Microwave Earth and Atmosp Sensing，1993：155－158.

［2］KRIEGER G，MITTERMAYER J，BUCKREUSS S，et al.Sector imaging radar for enhanced vision［J］.Aerospace Science and Technology，2003，7（2）：147－158.

［3］MITTERMAYER J，WENDLER M，KRIEGER G，et al.Data processing of an innovative forward looking SAR system for enhanced vision［C］／／EUSAR，2000：733－736.

［4］KRIEGER G，MITTERMAYER J，WENDLER M，et al.SIREV－Sector imaging radar for enhanced vision［C］／／Im－age and Signal Processing and Analysis，2001：377－382.

［5］陈 琦，杨汝良.机载前视合成孔径雷达Chirp Scaling成像算法研究［J］.电子与信息学报，2008，30（1）：228－232.CHEN Qi，YANG Ruliang.Research of Chirp Scaling imaging algorithm for air－borne forward－looking SAR［J］.Journal of Electronics ＆Information Technology，2008，30（1）：228－232.（in Chinese）

［6］任笑真，杨汝良.机载前视SAR三维成像算法研究［J］.电子与信息学报，2010，32（6）：1361－1365.REN Xiaozhen，YANG Ruliang.Study on three－dimensional imaging algorithm for airborne forward－looking SAR［J］.Journal of Electronics ＆Information Technology，2010，32（6）：1361－1365.（in Chinese）

［7］侯海平，曲长文，苏 峰，等.阵列LFMCW SAR模糊函数分析［J］.信号处理，2010，26（12）：1787－1794.HOU Haiping，QU Changwen，SU Feng，et al.Ambiguity function analysis of array LFMCW SAR［J］.Signal Processing，2010，26（12）：1787－1794.（in Chinese）

［8］梁 毅，王虹现，张 龙，等.基于二维Chirp－Z变换的前视FMCW雷达成像新方法［J］.中国科学：信息科学，2010，40：719－731.LIANG Yi，WANG Hongxian，ZHANG Long，et al.New method for forward－looking FMCW radar imaging based on 2－D Chirp－Z transform［J］.Science China：Information Science，2010，40：719－731.（in Chinese）

［9］耿淑敏，江志红，皇甫堪.基于改进Frequency Scaling算法的FM－CW SAR信号处理［J］.信号处理，2008，24（6）：951－956.GENG Shumin，JIANG Zhihong，HUANGFU Kan.Signal processing of FM－CW SAR using the modified Frequency Scaling algorithm［J］.Signal Processing，2008，24（6）：951－956.（in Chinese）

［10］MITTERMAYER J，MOREIRA A，LOFFELD O.Spotlight SAR data processing using the frequency scaling algorithm［J］.IEEE Trans on Geoscience and Remote Sensing，1999，37（5）：2198－2214.

［11］JIANG Zhihong，HUANGFU Kan，WAN Jianwei.Modified frequency scaling algorithm for FMCW SAR data processing［J］.Chinese Journal of Aeronautics，2007，20（2）：339－345.

［12］黄海风，董 臻，梁甸农.星载双站SAR“停走停”假设误差分析［J］.电波科学学报，2006，21（6）：863－867＋878.HUANG Haifeng，DONG Zhen，LIANG Diannong.Error analysis of“stop and go”hypothesis of spaceborne bistatic SAR［J］.Chinese Journal of Radio Science，2006，21（6）：863－867＋878.（in Chinese）

［13］CUMMING I G，WONG F H.Digital processing of synthetic aperture radar data：algorithms and implementation［M］.Artech House，2005：72－75.

［14］侯海平，曲长文，周 强，等.机载下视阵列SAR等效相位中心分析方法研究［J］.仪器仪表学报，2010，31（9）：2154－2160.HOU Haiping，QU Changwen，ZHOU Qiang，et al.Research on equivalent－phase－center analysis approach of airborne downward－looking array SAR［J］.Chinese Journal of Scientific Instrument，2010，31（9）：2154－2160.（in Chinese）