降雨粒子电磁特性分析及雨区目标成像
陈嘉琪 陈如山,2 彭 华 沈 鹏 丁大志
(1.南京理工大学通信工程系,江苏 南京210094;2.空间微波技术国防科技重点实验室,陕西 西安710000)
1.引 言
众所周知,电磁波能量沿传播路径传播时会出现散射和衰减[1]。这是因为当电磁波投射到气体分子或液态、固态的云和降雨粒子上时,一部分能量被散射,另一部分能量被吸收而转变为热能或其它形式的能量。实际的观测结果表明,随着波长的增加,雨水对雷达波的衰减迅速减小。所以虽然降雨粒子对波长较短的电磁波的散射更强,但是电磁波所受的衰减也更加严重。
合成孔径雷达(SAR)[2]是一种高分辨的成像雷达,具有可变视角、大范围观测及良好的穿透能力等特点,因此在军事和民用领域具有十分广阔的研究和应用前景。SAR系统通常被认为不受气候和昼夜影响,具有全天候、全天时的工作能力。然而,事实上当雷达工作频率高于3GHz时,各种气象粒子的影响就不得不加以考虑了[3]。特别在恶劣的天气状况下,雨雪、云层等气象粒子对较高频率的电磁波存在相当强的衰减作用[4]。因此,分析降雨衰减对SAR成像的影响具有重要的研究价值。
首先简明阐述了传输矩阵方法[5]的基本原理,分析了Ku、Ka波段下,降雨粒子的散射衰减特性,研究了宏观雨区模型中不同波段、不同雨强下的降雨衰减特性。结合上述雨衰模型、物理光学方法和距离多普勒成像算法,提出了一种雨区三维复杂目标的SAR成像仿真方法,该研究对未来针对复杂气象环境背景下的目标成像与识别具有重要的意义。
2.降雨粒子散射衰减特性仿真
T矩阵法又称扩展边界条件法(EBCM)、零场法,是求解表面积分方程的方法之一。由P.C.Waterman[6]于1965年首次引入计算电磁学领域,其基本原理是:粒子在入射场的作用下,表面产生电流,电流激发形成散射场。他定义了一个联系入射波和散射波的纽带——T矩阵。对于任意形状的散射体,总存在一个紧包着散射体的球面,将球面外法向方向的散射场Es(r)按照基底Ψ(r)分解,得到展开系数f,同样入射场Ei(r)也按基底RgΨ(r)分解,展开系数为a。展开系数间的关系由T矩阵给出。公式描述为[7]
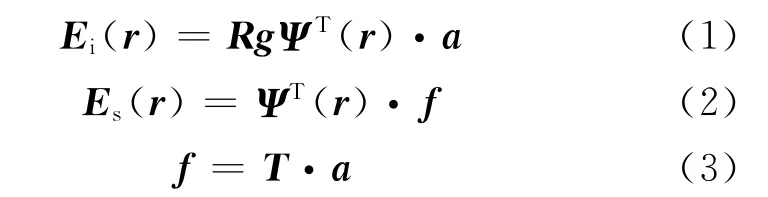
在该方法中,积分方程并不直接作用于散射体表面S上,而是加于如图1所示S之外的表面S1和S2上以简化方程的求解。下面,从数学角度阐述T矩阵方法的原理。
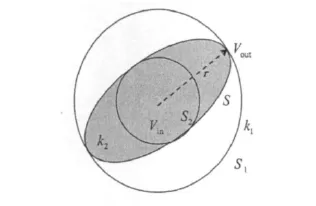
图1 求解T矩阵的模型示意图
假设入射平面波波数为k1,粒子内部的波数为k2,在球坐标系中,任意一点的坐标可以通过径矢r或者r={k1r,θ,φ}表示,其中r为该点到坐标系原点的距离,θ是极化角,φ表示方位角。粒子的尺寸参数通常采用电尺寸参数x=2πr/λ衡量。散射体中心位于原点,且散射体的形状通过函数R=R(θ,φ)描述。自由空间入射的平面电磁波可以表示为

式中:ninc是与波前相垂直的单位矢量;r表示距离向量。根据 Waterman的理论,可以将入射波和散射波都用球矢量波函数(VSWF)进行展开,且有
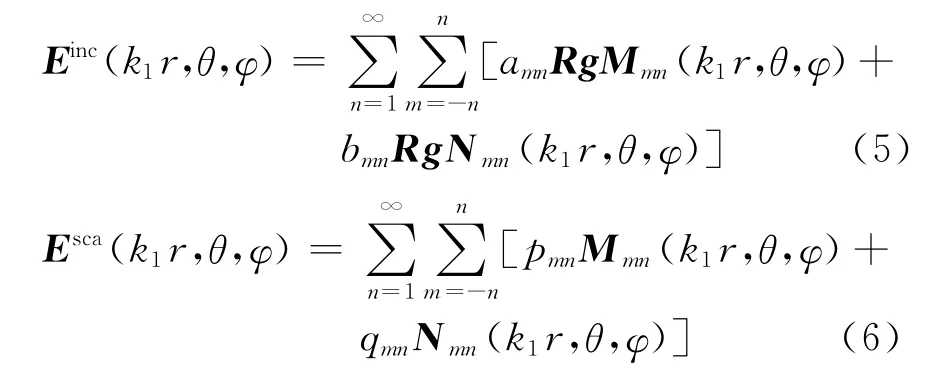
式中:RgMmn(k1r,θ,φ),RgNmn(k1r,θ,φ),Mmn(k1r,θ,φ),Nmn(k1r,θ,φ)和amn,bmn,pmn,qmn分别代表球矢量波函数和相对应的展开系数。其中,驻波函数RgMmn(k1r,θ,φ),RgNmn(k1r,θ,φ)在原点处是有穷的,并能简洁的表示入射场和内部场。外向行波波函数即谐波函数 Mmn(k1r,θ,φ),Nmn(k1r,θ,φ)能够确保散射场在无限远处满足辐射条件。参考文献[8]-[9]给出了采用扩展边界条件方法(EBCM)求解任意散射体T矩阵的简要数学推导。理论上,通过这些推导可以得到任意散射目标的T矩阵。
同一降雨粒子模型对于不同波段入射波的电磁散射特性往往存在很大的差别,针对同一降雨粒子模型在不同波段下的电磁特性进行对比分析。仿真结果的计算环境为:主频2.93GHz的Pentium(R)4CPU、1GB内存、Windows XP SP3操作系统。图2为降雨粒子坐标关系图。其中,Ei为入射方向,Es为散射方向。降雨粒子取向为θp=0°,其中θp为粒子旋转对称轴与笛卡尔坐标系z轴的夹角,并且位于x-z平面内;入射波方向为θi=Φi=0°,散射角θ是入射波方向与散射波方向的夹角,这里只考虑散射方位角位于x-z平面内的情况。图3为利用T矩阵方法和矩量法(采用经典的PMCHWT方程求解)针对椭球型降雨粒子模型在固定取向下散射强度的角分布。考虑到椭球降雨粒子具有空间非对称性,因此,首先考虑固定取向粒子的散射特性。粒子参数设置为:实际降雨粒子尺寸相同,x=2πreff/λ,reff为等效体积半径,大小为4.15mm.扁平回转椭球体的水平轴为旋转轴的两倍,即a/b=2,其中,a表示椭球粒子的水平轴,b代表椭球粒子的旋转轴。Ku波段下扁椭球粒子复折射指数m=1.784+0.00075i,等效电尺寸x=1.181,Ka波段下扁椭球粒子复折射指数m=1.784+0.0013i,等效电尺寸x=3.1748。
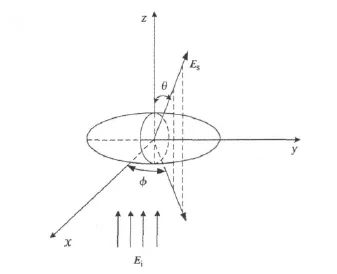
图2 降雨粒子坐标关系图
从图3可以看出,无论是水平极化波还是垂直极化波,Ka波段下降雨粒子的散射强度总体都要大于Ku波段下粒子的散射强度,并且其波动幅度明显要强于Ku波段。图3还表明,粒子的水平极化与垂直极化散射曲线存在明显的差异,垂直极化下的曲线波动更为剧烈。这意味着二者包含的降雨粒子的结构信息不同。
对于微波遥感而言,降雨粒子在空间的方位通常是随机的,这时仅仅研究某个固定方位下粒子的散射特性便不能满足实际情况的需要。随机方位下的粒子散射场可以通过对大量固定方位下粒子散射场取平均得到,但是这种方法需要耗费大量的计算时间和内存。M.I.Mishchenko提出了一种新的方法避免求解大量固定方位下的散射场,更为详细的方法描述请见参考文献[10]。

下面采用这种方法进行相应的仿真实验。仿真参数设置如下:降雨粒子模型轴比a/b=2。Ku波段下降雨粒子等效电尺寸x=1.181,复折射指数m=3.0+0.45i,Ka波段下降雨粒子等效电尺寸x=3.1748,复折射指数m =2.85+0.325i。仿真结果如图4所示。

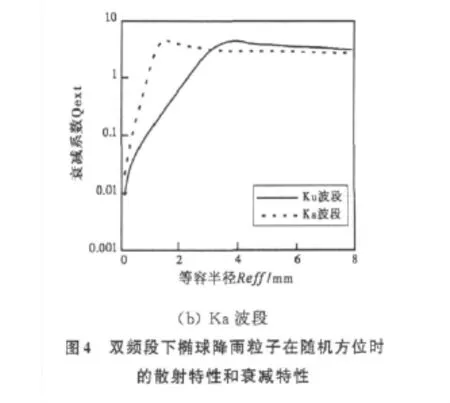
由图4(a)可以看出,散射角在0°~40°范围内,相同尺寸的降雨粒子在Ka波段下的相对散射强度比在Ku波段下大,在40°~180°范围内,则情况相反。两个波段下的相对散射强度曲线都比较平缓,没有大的振荡。从图4(b)中可以看出,在降雨粒子尺寸较小时Ku波段下的衰减系数比Ka波段下小很多,并随着降雨粒子尺寸的增大趋于某一固定值。在真实降雨的背景下,雨滴等容半径尺寸一般都小于3mm,由此可见,一般情况下Ka波段的衰减系数明显高于Ku波段,产生很强的雨衰效应。频率的增高使降雨衰减值也随之加大,其主要原因是随着频率的增高,其波长越来越接近于雨滴的尺寸。这样就加大了雨滴对电磁波的吸收和散射,继而增大了降雨衰减。而对于恶劣灾害天气(如:暴雨、冰雹),粒子尺寸很大时,降雨粒子对两种波段的衰减效应基本一致。
3.雨区目标成像仿真
上文从微观角度说明了Ku、Ka双波段的不同散射、衰减特性。下面,我们从更接近实际的雨区模型出发,从宏观角度对Ku、Ka双波段雷达信号的不同衰减特性进行分析。
在均匀降雨的条件下,雨衰的计算是相对简单的。然而在大多数实际的情况下,降雨在时间和空间上都是不均匀的,降雨非均匀的特点使得精确地计算雨衰变得十分困难。与此同时,雨媒质的非均匀性和随机性,又使得这一问题进一步复杂化。近年来,诸多学者通过不懈努力,结合理论分析和大量实验,建立起方便而且实用的经验公式,本文采取赵振维等学者提出的分频段雨衰减率解析模型[11]对随频率和雨强变化的单位衰减率曲面进行了仿真。
由图5给出的降雨单位衰减曲面可以看出,总体上,单位雨衰随着降雨的加强和频率的升高而增大。低频段(10GHz以下)降雨衰减不太严重,而对于较高频段,如Ku、Ka波段下的雨衰均不可忽略,特别在Ka波段下,电磁波波长与降雨粒子尺寸在同一数量级,其衰减幅度随着雨强增大迅速加大。因此,此时雨衰对合成孔径雷达(SAR)系统的影响便不可忽略。
下面本文采用一个经典的雨区模型[4]用于分析不同波段下降雨对合成孔径雷达图像的影响,如图6所示。其中,降雨区域的高度为4km,雷达俯仰角为60°。通过采用文献[11]描述的雨衰模型,我们可以获得任意频率、任意雨强下该雨区的降雨衰减。仿真中三维目标的雷达回波由物理光学方法[12]获取,成像方法为距离多普勒算法[2]。
仿真中的三维目标为F-15战斗机模型,如图7所示,相应的仿真波段为Ku和Ka波段,中心频率分别为15GHz和30GHz,带宽均为600MHz.
观测目标在Ku和Ka波段下,方位角为0°时的雨区成像结果分别如图8、9所示。由图8的仿真结果我们可以看出:当频率位于Ku波段时,小雨情况下(雨强为2mm/h)的雨衰影响仍旧不大,但当雨强为中等以上时,雨衰的影响便不可忽略了。特别在大雨情形下,Ku波段的SAR图像将呈现出明显的模糊状况。
Ka波段的雨区成像仿真结果如图9所示。从中可以看出,在这个波段下,即便是小雨也会对SAR图像产生一定影响。相应的,中雨时Ka波段的雨衰影响在图像上便已十分严重。而当大雨时,SAR图像将几乎完全被湮没。
4.结 论
本文从理论研究的角度出发,首先针对降雨粒子在Ku和Ka波段下的散射衰减特性进行了研究,从中我们可以看出:降雨粒子的水平极化与垂直极化散射曲线存在显著差异,这说明二者包含的降雨粒子的结构信息不同。与此同时,Ka波段下的电磁波波长与降雨粒子尺寸在同一数量级,其散射强度明显高于Ku波段。
之后,本文研究了不同雨强、不同频率下的降雨衰减模型,最终提出了一套结合雨衰模型、物理光学方法和距离多普勒成像算法,针对雨区三维复杂目标进行成像仿真的技术,并对Ku、Ka波段下的雨区雷达成像结果进行了仿真和分析。从中我们发现,中等以上强度的降水将对Ku波段下的SAR图像产生明显影响;Ka波段的SAR图像对降雨十分敏感,中雨时Ka波段的雨衰影响在图像上便已十分严重。而当大雨时,SAR图像将彻底模糊。
[1]张培昌,杜秉玉,戴铁丕.雷达气象学[M].2版.北京:气象出版社,2001.
[2]CUMMING I G,WONG F H.Digital Processing of Synthetic Aperture Radar Data:Algorithms and Implementation[M].Norwood,MA:Artech House,2005.
[3]DANKLMAYER A,D?RING B J,SCHWERDT M,et al.Assessment of atmospheric propagation effects in SAR images[J].IEEE Trans.Geoscience & Remote Sensing,2009,47(10):3507-3518.
[4]DANKLMAYER A,Madhukar C.Precipitation effects for X-and Ka-band SAR[C]//8th European Conference on Synthetic Aperture Radar(EUSAR).Aachen,Germany,2010:1-4.
[5]PETERSON B.T matrix for electromagnetic scattering form an arbitrary number of scatters and representation of E(3)[J].Phys.Rev.D,1973,8:3361-3677.
[6]WATERMAN P C.Symmetry,Unitary,and geometry in electromagnetic scattering[J].Phys.Rev.D,1971,3:825-839.
[7]聂在平,方大纲.目标与环境电磁散射特性建模-理论、方法与实现(应用篇)[M].北京:国防工业出版社,2009.
[8]GUGGENHEIMER H.Differential Geometry[M].New York:Dover Publications,1977.
[9]黄兴忠,金亚秋.任意取向非球形群聚粒子极化散射及其数值模拟[J].电波科学学报,1996,11(3):7-13.Huang Xingzhong,Jin Yaqiu.Numerical T-matrix solution for polarized scattering from a cluster of spatially-oriented,non-spherical scatterers[J].Chinese Journal of Radio Science,1996,11(3):7-13(in Chinese)
[10]MISHCHENKO M I.Light scattering by randomly oriented axially symmetric particles[J].J.Opt.Soc.Am.A,1991,8(6):871-882.
[11]ZHAO Zhenwei,ZHANG Minggao,and WU Zhensen.Analytic specific attenuation model for rain for use in prediction methods[J].International Journal of Infrared and Millimeter waves,2001,22(1):2001.
[12]KELLER J B.Geometrical theory of diffraction[J].J.Optics Soc.of America,1962,52(2):116-130.

