与或非功能树的功能集族求解方法

唐益明， 刘晓平



与或非功能树的功能集族求解方法

唐益明， 刘晓平

（合肥工业大学计算机与信息学院可视化与协同计算（VCC）研究室，安徽合肥 230009）

当前概念设计中与或非功能树的组合求解方法存在解空间庞大、冲突定位困难的问题，对此提出一种功能集族求解方法。定义了功能集族和广义与或树，基于经典命题逻辑理论将与或非功能树转化为等价的广义与或树，并通过求解功能集族实现了与或非功能树的功能求解算法。通过实例证明：该方法可有效地提高设计者的设计效率。

计算机应用；功能集族求解；经典命题逻辑；功能树

产品设计是一个复杂的创造性生产过程，其中概念设计是产品设计过程中最初的也是最具创造性的阶段。而“功能”这个概念贯穿概念设计的各个阶段, 它是概念设计的最基本元素。一般概念设计主要可以划分成两个阶段：① 功能分析，确定某个抽象层次的功能，分解功能，建立功能树和功能结构；② 功能求解，对每个分功能进行求解，得到分功能原理解，并组合形成设计方案。

与或非功能树是一种应用广泛的功能分析方法。文献[5]中提到基于公理化设计，将功能域向结构域的曲折映射表示为产品结构树，其自上而下是“功能―结构―子功能―结构―…”的不断分解过程。不过其过程是一个“与”分解的过程，并未涉及“或”分解的问题。文献[6]中将行为域引入到公理化设计，采用功能―行为―载体（结构）的域结构模板，并通过功能层、行为层、载体层交替出现的与或功能树来实现。文献[7]中建立了基于“需求域―功能域―原理解域循环映射”的概念设计模型，并提出了概念设计与/或树形式化表达方法。文献[8]基于相似理论和可拓学理论，针对与、或、非分解的功能树进行相似扩展研究。文献[9]首先总结当前已有的功能树，得到了一般意义的与或非功能树，并且针对与或功能树提出一种基于功能矩阵的功能求解方法，其中也考虑了简化问题。

目前，功能树的功能求解主要是通过组合原理来进行计算的。但对于规模较大的功能树，存在两方面的问题：一方面，其结构的复杂性无法让设计人员轻易地理清头绪，而且其功能的实现方案数极其庞大，导致很难准确寻找出最优解。另一方面，创新推理是概念设计的本质，而创新推理的主要难点在于冲突的检测、定位与消解。但对于规模较大的功能树，组合求解所得到的庞大的解空间，使得设计者很难迅速发现并定位冲突所在，更难以消解冲突。

为此，作者在文献[12]中针对与或功能树，基于布尔代数理论，提出了一种基于功能集族的功能求解方法。但是，其研究仅针对与或功能树，而对于与或非功能树，则并未涉及。

由于布尔代数与经典命题逻辑之间恰好存在着密切的联系，例如，经典命题逻辑中通过逻辑等价导出的Lindenbaum代数是布尔代数，命题公式与布尔函数之间可相互导出等。而且，创新推理作为逻辑推理的子问题，可见，从经典命题逻辑出发更有利于对与或非功能树开展研究。

因此，本文针对与或非功能树，研究基于功能集族的功能求解方法，基于经典命题逻辑理论对与或非功能树进行形式变换，并得到功能集族，以此作为设计解空间的表示。实践证明，该方法大量地缩减了解空间，对于冲突的发现与定位起到积极的推动作用。

1 与或非功能树的相关定义

与或非功能树可视为经典命题逻辑理论的一种应用。“与”门分解相当于“”，或门分解相当于“”，“非”门相当于否定运算“”。对于功能，若按或门展开为和，则有，即功能实现或功能实现，则有功能实现，其余类似可得。

定义1 对于与或非功能树中重复的叶子节点，用经典命题逻辑的原子公式来进行表示，称其为基本变量，记为。当基本变量对应叶子节点的需求实现时取1，否则取0。类似地，将功能树中门节点用逻辑公式表示，称为扩展变量。基本变量和扩展变量统称为树变量。记顶节点为的功能树为，并记功能树的层数为。

目标树函数本质上是把与或非功能树和经典命题逻辑映射起来的纽带，一方面是功能树结构的表示，一方面其计算都是按照经典命题逻辑运算规则。对功能树自上而下，通过与、或、非展开，直至叶子节点，则可得目标树函数。如图1为功能树的示例，其目标树函数为

2 与或非功能树的功能集族求解算法

定义5 在与或功能树中，如果将基本变量集拓展成为广义基本变量集，即叶子节点既可是基本变量，也可是基本变量的否定，则得到一种新的与或功能树，称其为广义与或树。

作者在文献[12]中针对与或功能树给出了功能集族求解算法。显然，与或非功能树不能直接利用其中算法。但是，如果设法将与或非功能树转化为广义与或树，则可较充分地利用文献[12]的算法。注意到对于与或非功能树，一般总可以假设其节点数有限。以下定理1证明了与或非功能树可以在保持逻辑等价的情况下转化为广义与或树。

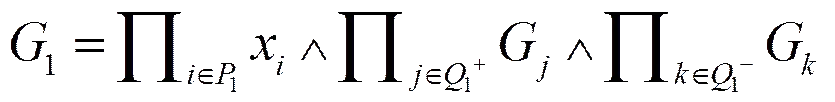
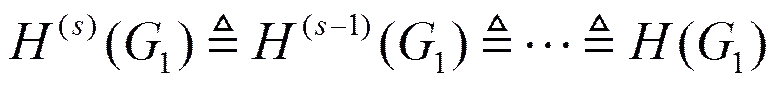
由定理1可得到从与或非功能树到广义与或树的转化算法，如算法1。

算法1 从与或非功能树到广义与或树的转化算法

Step8 结束。

在转化为广义与或树之后，可利用文献[12]中算法进行处理。在得到的功能集族中，若其中功能集满足：，则从经典命题逻辑理论的角度，需将该功能集删除。且基本变量集合从拓展到，即需适当调整文献[12]中算法。这里限于篇幅，不对其进行重新描述。

3 实 例

针对多功能茶杯的概念设计，假设由领域专家建立功能树如图2所示。如果从实现解的方案的组合数而言，考察本功能树的一个中间计算过程

可见，结果仅需考虑9个设计方案，而不用考虑由组合原理得到的480种方案。对于设计问题来说，由功能集族求解得到的求解方案，包含了最终的设计解。如其中的，可在此基础上得到解：杯身、杯盖采用双层中空结构，杯身可伸缩，采用内滤盖进行隔离。这里简化的效果取决于基本变量重复的次数和功能树的结构。其中，功能树的结构情况比较复杂，而功能树的节点重复次数越多，则简化的效果越好，反之亦然。尤其在没有基本变量重复的情况发生时，则完全退化为一般组合原理的方法。由此可见，采用本文方法可使设计者在原来大量冗余的方案中摆脱出来，能从优化后的方案中迅速找到功能求解方法；同时，可快速地定位冲突的关键之处，从而为冲突的检测、提取及消解提供了极大的便利性。因此，既有效缩减了解空间，提高设计效率，也对创新推理起到了积极的推动作用。

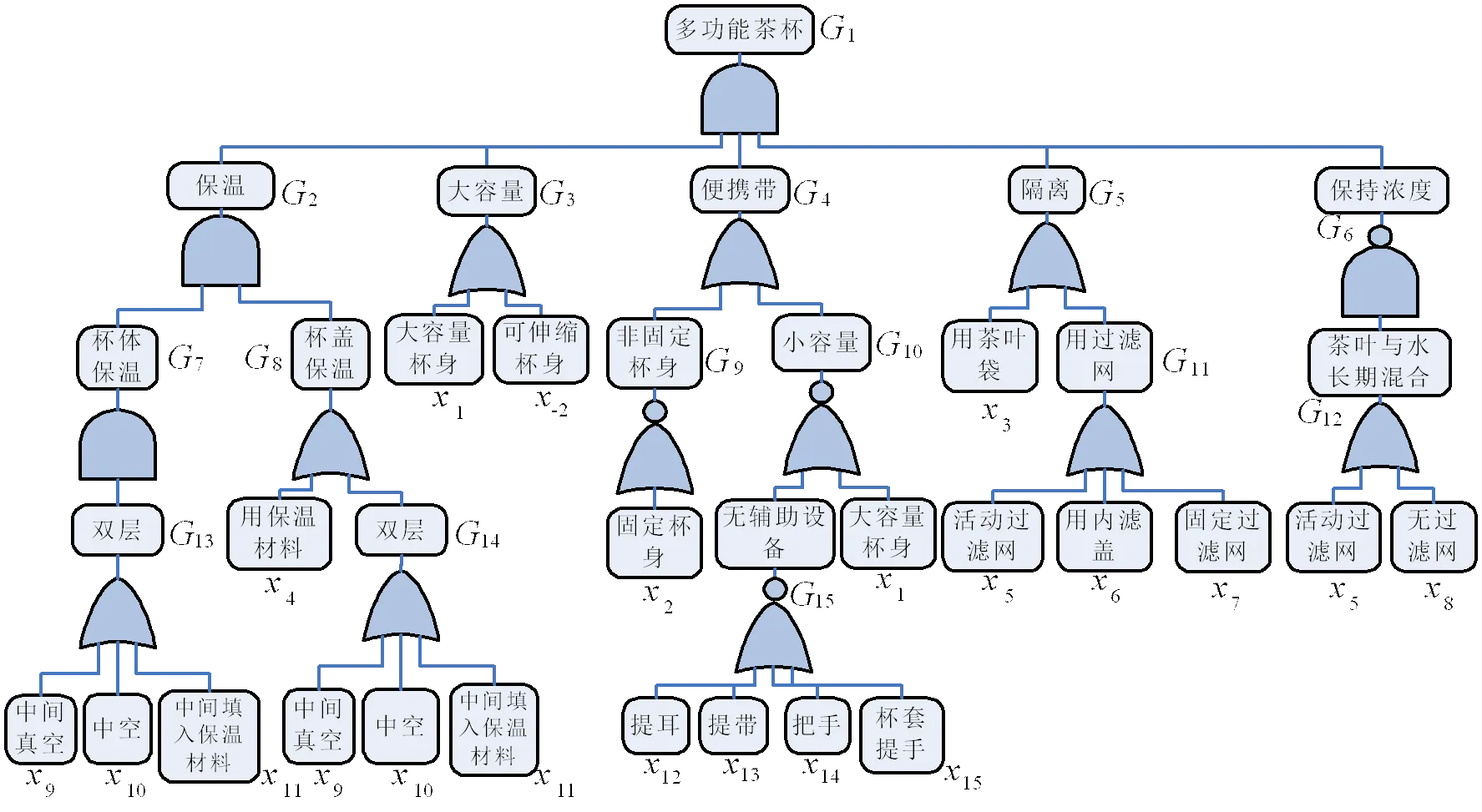
图2 功能树分解图

4 总 结

本文针对与或非功能树，提出基于功能集族的功能求解方法，将把功能树的功能求解转化为对功能集族的求解。该方法大量地缩减了解空间，对于冲突的发现与定位起到积极的推动作用,相比概念设计中常用的组合原理方法，可有效地提高设计者的设计效率。

当然，采用功能集族进行求解的方法也存在着一些缺陷和不足。由于经典命题逻辑的相关简化理论，使用这种简化方法可能会使一些基本信息发生丢失，这实际上就丢失了一批问题的求解方式，所以会导致设计解空间的缩小，可能存在损失。如何分析并消除这些损失，是下一步的工作重点之一。

[1] Hsu W, Liu B. Conceptual design: issues and challenges [J]. Computer-Aided Design, 2000, 32(14): 849-850.

[2] 孙守迁, 黄 琦, 潘云鹤. 计算机辅助概念设计研究进展[J]. 计算机辅助设计与图形学学报, 2003, 15(6): 643-650.

[3] Stone R, Wood K. Development of a functional basis for design [J]. Journal of Mechanical Design, 2000, 122(4): 359-370.

[4] Amaresh Chakrabarti, Thomas P Bligh. A scheme for functional reasoning in conceptual design [J]. Design Studies, 2001, 22(6): 493-517.

[5] 朱龙英, 朱如鹏, 刘正埙. 公理化设计与DFA集成的产品信息模型[J]. 计算机辅助设计与图形学学报, 2004, 16(2): 216-221.

[6] 宋慧军, 林志航. 公理化设计支持的概念设计产品模型[J]. 计算机辅助设计与图形学学报, 2002, 14(7): 632-636.

[7] 张 帅, 冯培恩, 潘双夏, 等. 基于循环映射模型的概念设计自动化策略研究[J]. 计算机辅助设计与图形学学报, 2005, 17(3): 491-497.

[8] 刘晓平, 陆劲挺, 唐益明. 基于可拓学的对比相似功能树扩展方法[J]. 工程图学学报, 2009, 30(1): 153-159.

[9] 刘晓平, 唐益明, 秦 晋, 等. 概念设计中基于扩展功能矩阵的功能求解方法[J]. 计算机辅助设计与图形学学报, 2007, 19(12): 1610-1617.

[10] Tang Yiming, Liu Xiaoping. Task partition for function tree according to innovative functional reasoning [C]//Proceedings of CSCWD 2008, IEEE Press, China, 2008: 189-195.

[11] 刘晓平, 唐益明, 秦 晋. 基于TRIZ的计算机辅助创新原型系统的研究与实现[J]. 工程图学学报, 2007, 28(6): 6-11.

[12] 秦 晋, 刘晓平. 基于功能集族的功能求解方法[J]. 工程图学学报, 2008, 29(5): 12-17.

A Function FamilySolving Method of And/Or/Not Function Tree

TANG Yi-ming, LIU Xiao-ping

( VCC Division, School of Computer and Information, Hefei University of Technology, Hefei Anhui 230009, China )

Combination solving is widely used for and/or/not function trees in conceptual design. However, there exist some serious problems such as enormous solving space and difficult conflict orientation in combination solving. A function family solving method is proposed. At first, the concepts of function families and generalized and/or trees are given. Furthermore, and/or/not function trees are equivalently converted to the generalized and/or trees based on classical propositional logic. At last, the function solving algorithm is realized by obtaining function families. The new method is proved to enhance designers’ work efficiency with an instance.

computer application;function family solving; classical propositional logic; function tree

TP 391.72

A

1003-0158(2011)01-0143-05

2009-05-06

国家自然科学基金资助项目（60673028）

唐益明（1982-），男，安徽无为人，博士研究生，主要研究方向为多值逻辑与模糊逻辑，CAD，人工智能。