测量结果数据修约及速算法

刘湘桂 周星明/桂林市计量测试研究所

0 引言

按有关规范的规定，测量仪器的最小分度值d 的数值应遵循以下规则：

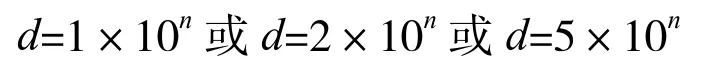
n为正整数、负整数或零。

因而测量结果经修约后的数据最末位的数值也应该相应的为 1×10n或2×10n或5×10n，经修约后的末位估读值应是1×10n-1或2×10n-1或5×10n-1。

1 数显读数装置及模拟读数装置测量结果修约的区别

数显测量仪器的测量读数不存在估读值，按相关的技术规范规定的程序测量n次，读取n个测量值，若取平均值作为测量结果，则平均值按四舍大于五入五凑偶的法则取舍末位，而后再对应测量仪器的最小分度值对经取舍后的平均值末位进行相应的修约。

若最小分度值是d=2×10n，则末位数值应修约为2、4、6、8、0（末尾数字应为偶数），例如用500 g砝码在分度值为2 g的电子秤上称量三次，读数分别为500 g、500 g、502 g,由于电子秤是直读数显仪器，不存在估读值，平均值只取到对应分度值那一位，即取平均值为501 g，电子秤的分度值d=2 g，不可能显示出501 g，因而平均值为501 g仍不能作为最终的测量结果，要对其对应分度值进行修约，其最终结果要么为500 g，要么为502 g，按修约规则是将此平均值乘以5，再按四舍六入五凑偶的法则取舍末位后除以5即为最终的作为测量结果的平均值。501×5=2 505，末位5前面的0为偶数，5不入舍去，2 505修约为2 500，2 500÷5=500，即取500 g为测量结果的平均值而不是取501 g。

若最小分度值是d=5×10n，则末位数值应修约为0.5，例如用100 kN标准负荷检测分度值为0.5 kN的数显压力试验机，三次测量读数分别为100.0 kN、100.5 kN、100.5 kN，平均值 100.3 kN，分度值为0.5 kN的数显压力试验机不可能显示出100.3 kN，要将此平均值乘以2，再按四舍大于五入五凑偶的法则取舍末位后除以2即为最终的测量结果的平均值。100.3×2=200.6 ≈ 201，201÷2=100.5，即取100.5 kN为测量结果的平均值而不是取 100.3 kN。

若最小分度值是d=1×10n，其末位从0～9的10个数字均可显示，则只要按四舍六入五凑偶的法则修约至对应数显仪器的最小分度值。

模拟读数装置的测量仪器测量读数末位为估读值，一般取最小分度值的十分之一作有效读数，小于最小分度值十分之一的值是难以读取而是没有实际意义的。因此测量结果的末位只取到最小分度值的后一位，并对应其进行相应的修约。

对于各种分度值的测量数据修约方法与上述方法相同。0.2单位修约的将拟修约的数乘以5，末位按规则取舍后再除以5，0.5单位修约的将拟修约的数乘以2，末位按规则取舍后再除以2。

例如用活塞压力计检定分度值为0.2 MPa的精密压力表，测量读数估读到0.2 MPa的1/10（即0.02 MPa的整数倍），标准压力值5 MPa点测量2次的读数分别为 4.98 MPa、5.00 MPa，平均值为4.99 MPa，末位 0.09 显然不是 0.02 的整数倍，要进行 2间隔的修约，4.99×5=24.95，按取舍规则24.95 ≈ 25.00，25.00÷5=5.00，取 5.00 MPa 为该点最终的测量值。以此类推5间隔的修约，将拟修约的数乘以2，末位按规则取舍后再除以2即可。

2 2、5间隔数据修约速算法

按规定的要求2间隔修约要乘以5取舍后除以5，5间隔修约要乘以2取舍后除以2，若有效位数较多时口算或心算难以做到，就要用笔算或借助计算器，数据处理的效率大大降低。笔者根据多年从事计量工作的实践经验，介绍一套非常实用的速算方法。

2间隔修约是对拟修约位的数值不是2的整数倍的数进行修约，如对 12.93 和 12.83（0. 2 分度模拟读数的平均值或0.02分度数显读数的平均值）进行修约，按规定的方法 12.93×5=64.65，按规则取舍后为 64.6，再除以 5 最后得 12.92，12.83×5=64.15，按规则取舍后为 64.2，再除以 5最后得12.84。速算法是将拟修约位的数除以2，把商的个位与拟修约位的前一位相加得奇数拟修约位加1（即往大取），若加得偶数则拟修约位减1（往小取）。12.93 和 12.83 拟修约位的数均为 3，3÷2=1.5，其个位1与前一位9相加得偶数，往小取得12.92；与前一位8相加得奇数则往大取得12.84。无需多位数的乘除, 一眼就能看出来。如 12.95, 5÷2=2.5, 2 ＋ 9 ＝ 11 是奇数 , 往大取得12.96；又如 12.85，5÷2=2.5, 2 ＋ 8 ＝ 10 是偶数 ,往小取得12.84。其结果与按规定步骤计算出的结果是一致的。

5间隔修约是对拟修约位的数值不是5的整数倍的数进行修约，速算法更简单，把拟修约位视为个位，拟修约位的值小于等于2.5的拟修约位取0，其值大于2.5而又小于7.5的拟修约位取5，而大于等于7.5的则进位，即拟修约位取0，其前一位加1。这里不再一一举例，读者可自行验证。