偏心支撑半刚性连接钢框架的动力特性研究

郭兵，吴永清

(1.山东建筑大学 土木工程学院，山东 济南250101;2.山东省公安消防总队，山东 济南250101)

0 引言

结构体系的动力特性(如周期、频率、阻尼比)是结构动力分析和抗震设计的基本参数，我国相关技术规范虽然提供了框架结构动力特性的参考值或简化计算方法，但都是针对传统的刚性连接框架的，未考虑梁柱节点刚度的影响。对于工程中实际存在的半刚性连接钢框架，国内外研究资料均表明［1－7］:梁柱半刚性连接使结构自振周期延长、阻尼增加，结构动力特性随着梁柱节点刚度的不同而变化，因此我国规范的相关规定不适用于半刚性连接钢框架。

由于半刚性连接钢框架的抗侧刚度相对较低，用于多高层建筑时一般需要设置抗侧力体系，将偏心支撑与半刚性连接钢框架相结合就是其中一种，也是一种新型抗震结构体系。目前国内外的相关研究刚刚起步，有关动力特性的研究资料暂未见到，问题亟待解决。针对上述情况，本文进行了偏心支撑半刚性连接钢框架的动力特性试验研究和数值模态分析，目的是找出影响结构动力特性的主要因素，并分析其影响规律，给出计算方法或参考值。

1 动力特性试验研究

针对工程中常见的梁柱节点类型，共设计了4个V型偏心支撑半刚性连接钢框架试件。试件为三层单跨单开间空间结构，按1∶2缩尺比例设计，层高1.5m，跨度3m，开间2m，考虑8度设防(加速度为0.2g)，试件尺寸见图1。试验的主要目的是研究梁柱节点类型、节点转动刚度对结构动力特性的影响，并与理论分析结果进行对比验证。

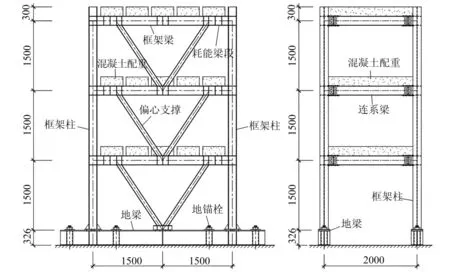
图1 空间框架试件的主要尺寸

表1 节点转动刚度及框架动力特性

框架梁、柱截面分别为 H200×130×6×8，H180×180×8×10，连系梁截面同框架梁，柱脚刚接;V型偏心支撑的截面为H100×100×6×8，两端与框架梁焊接连接;节点域柱腹板、剪切型耗能梁段均设置了加劲肋。所有构件的长细比、板件宽厚比以及节点域均满足现行规范的相关要求。

试件编号为FS1～FS4，各试件的区别仅是梁柱连接节点做法不同:FS1采用全焊接节点(图2a)，主要用来与其他试件进行对比;FS2采用外伸式端板螺栓节点(图2b)，端板厚20mm;FS3采用上下翼缘T型钢螺栓节点(图2c);FS4采用上下翼缘及腹板角钢螺栓节点(图2d)。

梁柱节点螺栓均为10.9级高强度螺栓摩擦型连接，抗滑移系数为0.35。试件的所有焊接工作均在工厂完成，高强度螺栓现场通过扭矩扳手紧固到位。除高强度螺栓外，试件全部材料均为Q235-B钢，实测屈服强度平均值为319N/mm2。

由于框架梁柱连接节点的转动刚度是主要影响因素，因此在制作框架试件的同时，也加工了相同尺寸、相同材料的节点试件，并先期进行了节点转动刚度试验，测得节点的初始转动刚度R值见表1。四类节点的转动刚度值范围较大，具有一定的代表性。

图2 各试件的梁柱节点图

框架试件现场见图3，框架柱与地梁刚接，每个地梁通过4个M80地锚栓与实验室地板连接。为了模拟楼面竖向荷载和质量，铺设了预制混凝土配重楼板，每层堆载30kN，框架梁上对应的线荷载为5.0 kN/m(不含结构自重)。每层楼面均设置角钢交叉支撑，以增加楼面刚度。

图3 框架动力特性测试现场

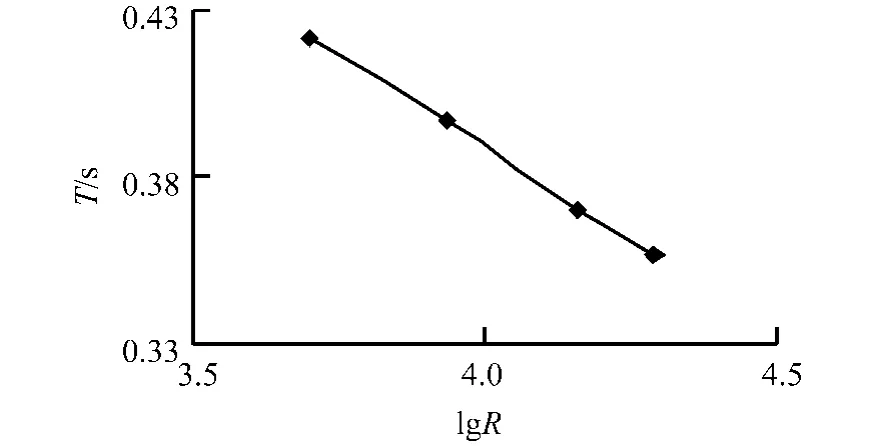
图4 lgR与T的关系

框架动力特性采用891-II型拾振器系统测试，每层楼板上都放置了传感器，采用橡皮锤激振，数据采集由891信号放大器、INV360U数据采集仪完成。测试结果见表1，可以看出:

(1)随着梁柱节点初始转动刚度的逐渐降低，框架结构自振频率依次减小，自振周期和阻尼比依次增加，主要是由于节点刚度降低使得结构的刚度降低，从而增加了结构自振周期。节点初始转动刚度的对数值与结构自振周期的关系见图4，基本为线性关系。

(2)实测结构自振周期介于0.356～0.422s之间，是框架层数的0.12～0.14倍。我国98版高钢规程提供的周期估算公式为T=0.1n(n为框架层数)，计算值显然略偏低。

(3)实测结构阻尼比介于0.035～0.044之间，我国2001版抗震规范建议的多层框架结构在多遇地震下的阻尼比为0.035，略偏低;2010版抗震规范做出了调整，建议多遇地震下高度不大于50m时可取0.04，位于本文实测数据范围之内。对于多层偏心支撑半刚性连接钢框架的阻尼比，本文建议取0.035～0.045，节点转动刚度较低时取大值，节点刚接时取 0.035。

2 有限元模态分析

2.1 有限元模型及验证

因试件数量有限，不足以反应全部问题，需要通过大量的数值分析来作为补充，本文借助ANSYS有限元软件采用模态分析方法完成。为准确建立有限元三维模型，框架梁、柱、支撑以及加劲肋等均采用SHELL181壳单元;框架梁柱之间的半刚性连接采用COMBIN39一维旋转弹簧单元和MPC184单元完成。COMBIN39单元的弯矩—转角关系可以根据节点的实际情况采用多点准确定义，见图5。建立半刚性节点时，梁柱之间留有微小的间隙，先用MPC184单元分别将梁端面、柱与梁的对应面进行刚化，再在两个面的刚性原点之间建立COMBIN39弹簧单元。为保证两个面的变形协调，还需要进行相关位移的耦合。

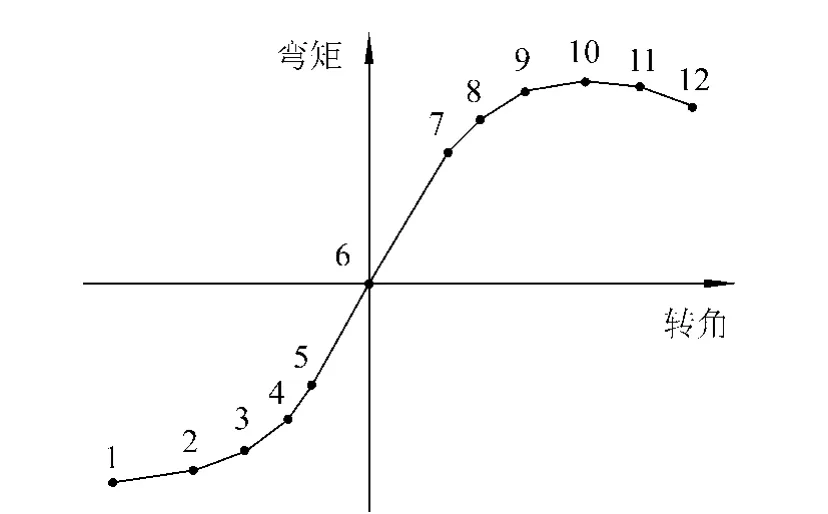
图5 COMBIN39单元弯矩—转角关系示意

为验证有限元方法的可靠性，对前面试验进行了模拟验证，各类参数(如材料本构关系、试件边界条件、质量、节点刚度等)均与试件完全相同，楼板的质量通过壳单元的实常数定义，利用“附加质量”选项施加到相应构件上。ANSYS计算结果与试验结果的对比见表1，与试验值相比，最大误差8%，验证了该方法的可靠性。

2.2 有限元试件及研究参数

影响结构自振周期的可能因素有:梁柱节点的初始转动刚度、偏心支撑类型、框架的层数，上述参数的取值情况分别如下:

(1)梁柱连接节点的初始转动刚度:分别取0、1×102，5 × 102，1 × 103，5 × 103，1 × 104，5 × 104，1 × 105，5 ×105，1 ×106，1 ×109，1 ×1012(单位:kNm/rad)，共12种情况。其中刚度为0时代表理想铰接，刚度为1012时属于无穷大，代表理想刚接，上述取值范围具有足够的代表性。因本文仅分析结构弹性阶段的自振周期，故只与节点初始转动刚度有关，与弹塑性刚度无关，但为了充分说明问题，仍输入节点的整条弯矩—转角曲线，采用郭兵提出的两线段模型［8］。

(2)偏心支撑类型:设计了无支撑、V型支撑、人字型偏心支撑、门式偏心支撑共四种情况，见图6，耗能梁段均为剪切型。

图6 偏心支撑的类型

(3)框架的层数:有6层、9层、12层、15层、18层共五种，均为单跨。

有限元框架试件采用PKPM软件设计完成，取跨度7.8m，层高3.9m，开间6m，柱脚刚接，具有典型代表性。试件主要设计参数、控制指标如下:楼面恒载取 4.0kN/m2，活载取 2.0kN/m2，周边考虑轻质砌块墙体，基本风压取0.45kN/m2;考虑8度抗震设防烈度(加速度0.2g)，设计地震分组为第一组，场地类别为Ⅱ类;全部试件都同时满足梁柱刚接、铰接两种要求，且构件应力比控制在0.8左右;钢材为Q235;框架梁、柱及支撑的长细比、板件宽厚比均满足抗震规范要求。空间框架设计完成后，取出一榀平面框架单元作为有限元试件，并在梁柱节点处施加平面外约束。有限元试件的单元划分由ANSYS自动完成，单元数量最多的为14088个。

2.3 有限元分析结果

以六层框架为例，不同支撑类型对结构自振周期的影响见图7，可以看出:

(1)随着节点初始转动刚度的增加，全部试件的自振周期都逐渐减小，主要是由于节点刚度的增加导致结构刚度也增加。

(2)当节点初始转动刚度小于103kNm/rad时，结构自振周期与节点刚度为0时基本相同，即可简化为梁柱铰接;当节点初始转动刚度大于5×105kNm/rad时，结构自振周期与节点刚度为无穷大时基本相同，即可以简化为梁柱刚接;当节点初始转动刚度介于103～5×105kNm/rad之间时，属于半刚性节点，此时节点刚度对自振周期的影响比较显著，不可忽略。

在半刚性范围内，节点初始转动刚度与结构自振周期基本为线性关系，与本文前面试验结论(图4)一致，也与文献［6］的研究结论相同。

(3)节点初始转动刚度对结构第一振型周期的影响最大，对高阶振型影响很小，可以忽略。

(4)与无支撑框架相比，有支撑框架的自振周期显著减小，降幅达70% ～80%，而且使得节点刚度对结构自振周期的影响也明显减小。主要是由于偏心支撑显著增加了结构的侧向刚度，降低了结构刚度对节点转动刚度的敏感性。

(5)偏心支撑的类型对结构自振周期略有影响，V型支撑的自振周期最大，人字形支撑的自振周期最小，门式支撑介于二者之间，但三者差别不足10%，可以忽略其影响。

图7 不同支撑类型时自振周期与节点刚度的关系

框架层数对结构自振周期的影响见图8，可以看出:随着层数的增加，结构自振周期逐渐增大，各曲线基本呈等间距平行关系。

图8 不同层数时自振周期与节点刚度的关系

为了充分说明层数与自振周期的关系，以六层人字形偏心支撑框架为例，节点刚度为定值时周期与层数的关系见图9，可以看出:无论节点刚度为何值，自振周期均与层数呈线性关系。因此，影响自振周期的最主要参数是框架层数，节点刚度的影响可以通过系数来表达。参考高钢规程的做法，结构自振周期T与层数n可以用下式计算:当节点刚度较低时，上式可以取大系数，节点刚度较大时可以取小系数。

图9 结构自振周期与层数的关系

3 结论

通过对偏心支撑半刚性连接钢框架这一新型结构体系的动力特性试验研究和有限元分析，可以初步得出以下几点结论:

(1)随着梁柱节点初始转动刚度的逐渐降低，框架结构自振频率依次减小，自振周期和阻尼比依次增加。与无支撑框架相比，有偏心支撑框架的自振周期降低了70%～80%，且节点刚度对结构自振周期的影响显著减小，说明偏心支撑降低了结构对节点刚度的敏感性。

(2)当梁柱节点初始转动刚度小于103kNm/rad时，可以简化为铰接;当初始转动刚度大于5×105kNm/rad时，可以简化为刚接;当初始转动刚度介于103～5×105kNm/rad之间时，属于半刚性连接。在半刚性范围内，结构自振周期与节点刚度基本为线性关系。

(3)节点转动刚度对第一振型周期的影响较大，对高阶振型的周期影响很小，可以忽略。

(4)随着框架层数的增加，结构自振周期线性增加，可采用(1)式进行结构自振周期的简化计算，现有规范的方法不再适用。

(5)多层偏心支撑半刚性连接钢框架的阻尼比可取0.035～0.045，节点转动刚度低时取大值。

［1］ELNASHAI A S，ELGHAZOULI A Y.Seismic behavior of semirigid steel frames［J］.Journal of Constructional Steel Research，1994，29(1 －3):149 －174.

［2］ELNASHAI A S，ELGHAZOULI A Y，DENESH-ASHTIANI F A.Response of semi-rigid steel frames to cyclic and earthquake loads［J］.Journal of Structural Engineering ASCE，1998，124(8):857－867.

［3］ASTANESH-AlS A.Seismic performance and design of bolted steel moment resisting frames［J］.Engineering Journal AISC，1999，36(3):105－120.

［4］孙修礼，梁书亭，王群依，等.半刚性连接框架结构的动力特性研究［J］.工程抗震与加固改造，2005，27(1):16 －18.

［5］郭兵，郭彦林，柳锋，等.焊接及螺栓连接钢框架的循环加载试验研究［J］.建筑结构学报，2006，27(2):47 －56.

［6］郭兵，郭彦林，李光明.半刚接钢框架的动力特性探讨［J］.建筑结构，2007，37(10):109 －111.

［7］马翠玲，孙颂旦，华建兵，等.半刚性连接钢框架频率的研究［J］.西安科技大学学报，2010，30(2):187 －191.

［8］郭兵，顾强.多层钢框架中梁柱端板连接的强度和刚度［J］.建筑结构学报，2004，25(2):27 －31.