小直径钢管排桩边坡加固计算理论研究

张正义

(铁道第三勘察设计院集团有限公司地路处，天津300251)

0 引言

小直径钢管桩一般指直径小于300 mm的插入式或灌注式钢管桩［1］，桩顶设置联系梁，形成各排桩协同工作的空间排架结构。这种空间排架体系使得桩与桩之间的相互联系得到加强，整体抗弯刚度增大，桩顶变形易得到控制，能充分发挥每一根钢管桩的工作潜力。所以近年来小直径钢管桩在工程实践中得到广泛应用，国内外相关研究相继出现。曾宪斌等［2］将小直径钢管桩与固结灌浆技术联合应用于岩溶地基处理中，取得了较好效果;张勇等［3］应用钢管微型桩对倾斜楼房进行了纠偏加固;Amhest Mass等［4］采用模型试验的方法，指出小直径钢管桩的应用可以提高桩周土体的粘聚力，使土的抗剪强度增强。但关于小直径钢管排桩体系加固边坡的计算理论研究不多，这严重制约了该结构的应用推广。为此，根据小直径钢管排桩的受力特点，通过对排桩简化成桩-岩土体-桩的相互作用模式［5］和作用力计算分析模型推导出排桩内力位移的计算公式。结合现场堆载试验，将试验测试数据与本文计算结果进行对比分析，二者吻合较好，从而验证了本文方法的正确可靠性。

1 计算理论

小直径钢管排桩按分段法计算内力及位移，边坡滑面以上桩体部分为受荷段，基本力系为滑坡推力和桩前抗力;滑面以下桩体为锚固段，产生锚固支撑抗力。

1.1 受荷段计算模型

以三排钢管桩为例，其平面布置如图1，在考虑桩间距作用前提下，将空间排架结构简化为平面刚架体系，建立桩土相互作用的计算模型［6-7］如图2，在滑坡推力q(x)及桩前抗力F(x)作用下，由桩顶联系梁+钢管排桩+桩间土+锚固段组成的整体系统共同作用，抵御边坡滑动。

由于桩间土与前后排桩相互作用主要是水平方向，故可将桩间土视为连接前后排桩的土弹簧，土压力由此弹簧与前后排桩的位移协调分配，弹簧刚度由桩间土的水平向地基反力系数K确定。

基本假定:钢管排桩所受滑坡推力和桩前抗力为三角形分布［8］;考虑桩土相互作用，将土体视为弹性体，桩间岩土体的抗力与相邻排桩的相对位移成正比，因此桩间岩土体分布函数q1(x)、q2(x)是关于桩身x的高次多项式，为了简化计算分析，将桩前抗力的分布形式等效为三角形分布荷载;钢管排桩与联系梁为刚性连接，滑动面处为固定端支座。

图1 平面排桩布置

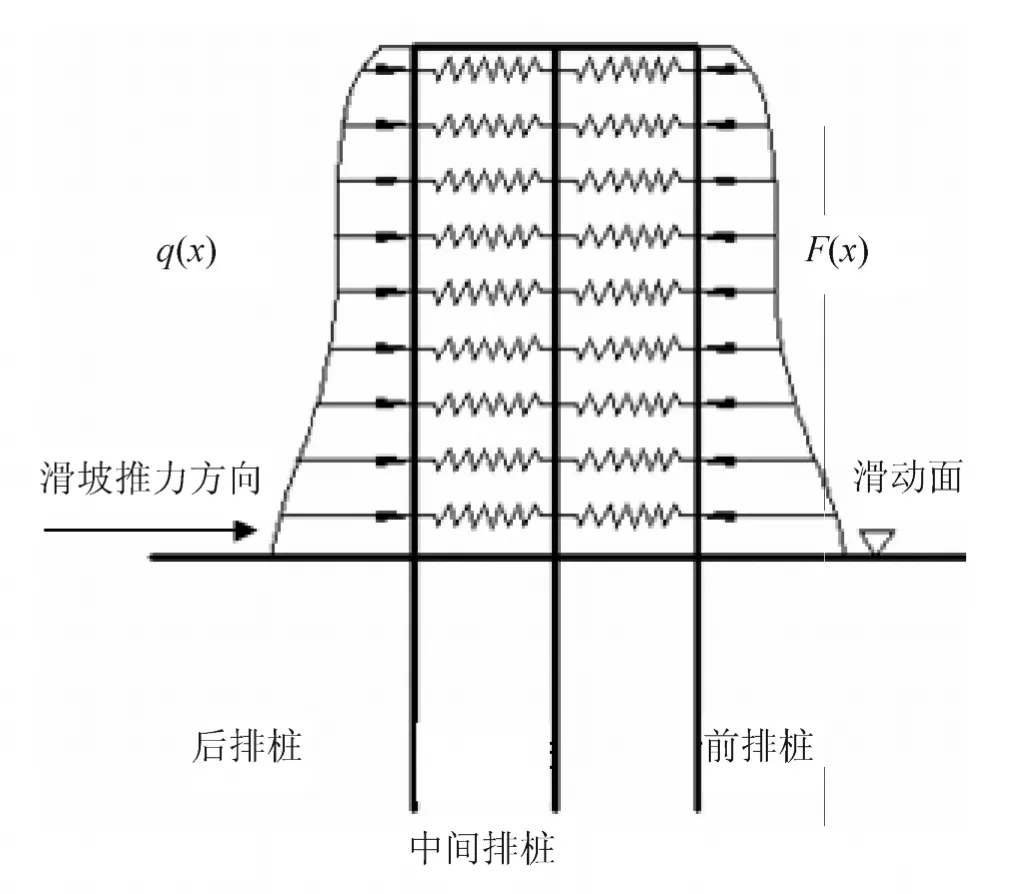
图2 排桩受荷段计算模型

根据以上基本假定，可将受荷段计算模型进一步简化如图3，图中q1、q2分别为AB与CD桩、CD与EF桩桩间作用力;P1、P2为各桩所受联系梁作用的剪力;M1、M2、M3为各桩所受联系梁作用的弯矩。

1.2 受荷段桩身内力位移计算

根据假定按“K”法计算受荷段桩身内力位移，设AB、CD、EF桩的位移方程分别为UAB、UCD、UEF，桩AB和CD之间的相对位移为Δu1(x)，桩CD和EF之间的相对位移为Δu2(x)，则

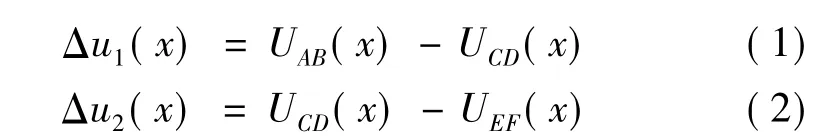
由Winkler弹性地基梁理论得

式中，q1(x)，q2(x)为桩前任意一点处的抗力;BP为桩的计算宽度;k为水平地基系数;K为水平抗力系数。

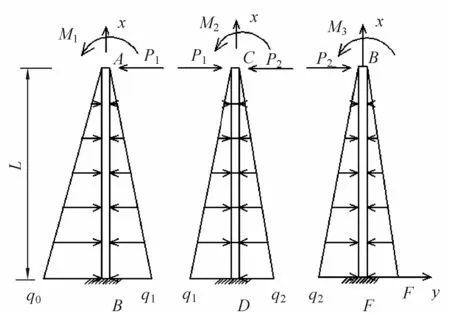
图3 排桩受荷段简化计算模型

由于通常两排桩之间土层的厚度很薄，当桩长大于排距的4倍时(即相当于大于桩间土厚度的5倍)，且每一排桩内的桩距不大时，一般可认为竖向薄层压缩［7］，于是水平抗力系数K可以简化为

式中，Es为桩间土的水平向变形模量(kPa);b为桩间土层的厚度，即排间净距(m)。钢管桩属弹性桩，符合位移叠加原理，按材料力学方法可得

式中，A(x)=x2(10L3－10L2x+5Lx2－x3)/(120EIL);B(x)=x2(3L－x)/(6EI);C(x)=x2/(2EI)。由排桩变位连续条件及边界约束条件可推得根据实际情况取值。

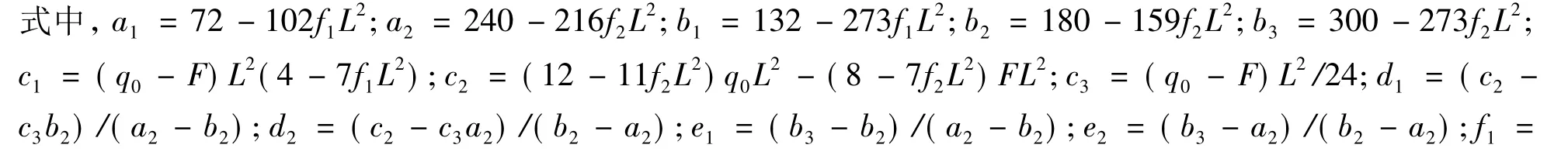
将(10)～(16)式代入(7)～(9)式可求出桩身位移，由结构力学方法可求桩身弯矩及剪力

1.3 锚固段内力及位移计算

小直径钢管桩属弹性桩，其锚固段的位移及内力按弹性地基梁“K”法计算，公式如下

式中，φ1=cosβy chβy;φ2=(sinβy chβy+cosβy shβy)/2;φ3=(sinβy shβy)/2;φ4=(sinβy chβy－cosβy shβy)/2;M0，Q0，x0，φ0分别为滑面处桩身弯矩、剪力、位移和转角。

2 工程实例分析

2.1 现场堆载试验

本文依托四川省广元至巴中高速公路木门段滑坡治理工程，在K100+070～K101+100段木门互通式立交桥左侧一级边坡采用小直径钢管排桩支挡工程为例，结合工点支挡工程设计方案见图1，选取下沿50 m左右处的线外场地进行堆载试验，试验场地剖面图见图4。钢管桩选用电焊直缝钢管，型号为140 mm×4.5 mm，接长采用内套管全熔透焊接，焊接强度同母材，内套管选用无缝钢管，型号为127 mm×5 mm，预成孔插管法施工，钻孔直径Φ180 mm，桩长12 m，锚固段长度为5 m。

为了清楚的认识小直径钢管排桩在堆载过程中的受力、内力和位移，对桩侧土压力、桩身位移、应变进行了现场监测。其试验方案如下:成孔后将土压力盒安装于孔内不同深度处，再用中砂分段冲水填实，测量桩侧土压力;在试桩的表面受滑坡推力侧布设表面应变计，每根试桩布设5根，监测桩身不同深度的应变;将测斜管插入钢管桩中央，管顶盖上顶盖，再向试桩内注浆监测桩身水平位移。土压力监测结果如图5所示。

由图5土压力监测结果可以发现滑动面以上各排桩土压力近似于三角形分布，与本文计算假设一致;桩后土压力值与桩间土压力值相差不大，这与钢管桩对滑坡反力的扩散作用有极大关系，可以认为在同一排桩之间形成了土拱，将桩间的滑坡推力平均分配到相邻桩上去。

2.2 本文方法计算

图4 堆载试验场地剖面图(单位:m)

图5 各排桩实测土压力

根据堆载试验现场资料，采用本文方法对桩身弯矩、位移进行计算，并将结果与现场实测结果进行对比分析。滑体土内摩擦角为φ=25°，滑面倾角为40°，由传递系数法计算桩后滑坡推力为560 kN/m，桩前剩余抗滑力为484 kN/m;滑面以上土体变形模量Es=10 000 kPa，桩长L=7 m，滑面以下地基抗力系数K=80 000 kN/m3。钢管桩三排桩矩形布置，排桩排距、间距均为1.5 m。

经计算，桩的抗弯刚度EI=2 358 kN·m2。

计算宽度，根据工程经验取5d，BP=5d=0.9 m。

土的抗力系数k=EsBP/b=6 000 kN/m3。

滑坡推力按三角形分布，则作用在桩上的滑坡推力为E=87.3 kN，则q0=25 kN。

把上述数值带入解析式可求得M1=12.1 kN·m;M2=18.2 kN·m;M3=20.8 kN·m;q1=13.7 kN/m;q2=6 kN/m;P1=3.1 kN;P2=2.4 kN。

把求得的值带入式(5)～式(7)及式(15)～式(19)可求得桩身位移及内力。计算结果如图6和图7。

现场采用侧斜管测量桩身位移，而采用应变计测量桩身应变ε的方式间接测量桩身弯矩，换算公式

2.3 结果对比分析

图6可以发现滑面处弯矩即最大弯矩值大于实测值，设计时偏于安全;理论值两种弯矩曲线的变化趋势一致，理论值与实测值吻合较好，验证了本文计算方法的正确性。

由图7可以看出最大位移出现在桩顶位置处，滑动面以下位移很小，且锚固段桩底以上部分有两个位移零点，桩底位移为零，这符合小直径钢管桩单桩抗弯刚度较小的理论;理论位移值略大于实测值，按这种理论计算偏于安全;在滑动面处钢管桩的位移变化趋势要比理论计算变化趋势要大，可能是由分段计算导致位移叠加造成。理论计算位移曲线与实测位移曲线相当吻合，可以认为该理论计算方法可行。

2.4 荷载分担比计算

由桩间土体抗力的值q1和q2即可求出每根桩承担的荷载和荷载分担比。例如后排桩AB承担的荷载EAB为EAB=(q0－q1)L/2=39.55 kN。则AB桩的荷载分担比为=(EAB/E)×100%=45.3%。

同理可以计算出桩CD和桩EF承担的荷载及荷载分担比，计算结果如下:

ECD=27 kN;=30.9%;EEF=21 kN;=23.8%。则，∶∶=0.453∶0.309∶0.238。

3 排桩加固边坡的影响因素分析

3.1 桩体刚度影响

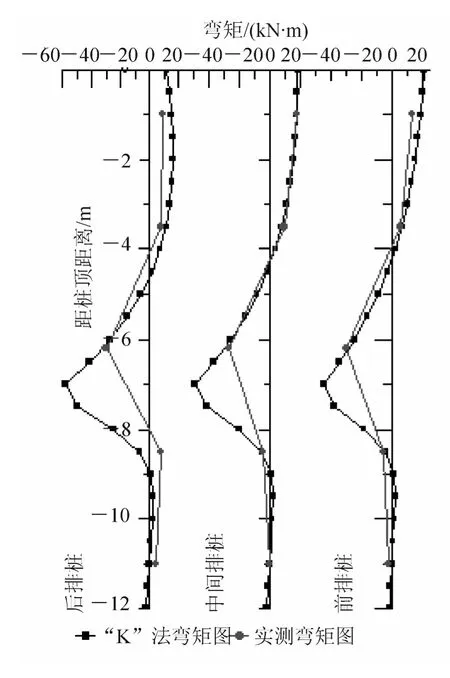
图6 弯矩对比

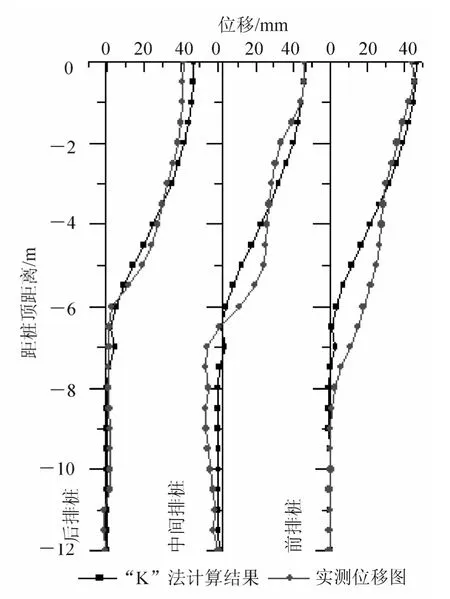
图7 位移对比

桩体刚度的大小直接影响到钢管桩的直径和壁厚，进而会影响到工程造价，所以下面讨论钢管桩的刚度对荷载分担比和桩顶位移的影响。桩体刚度变化对比分析如表1。

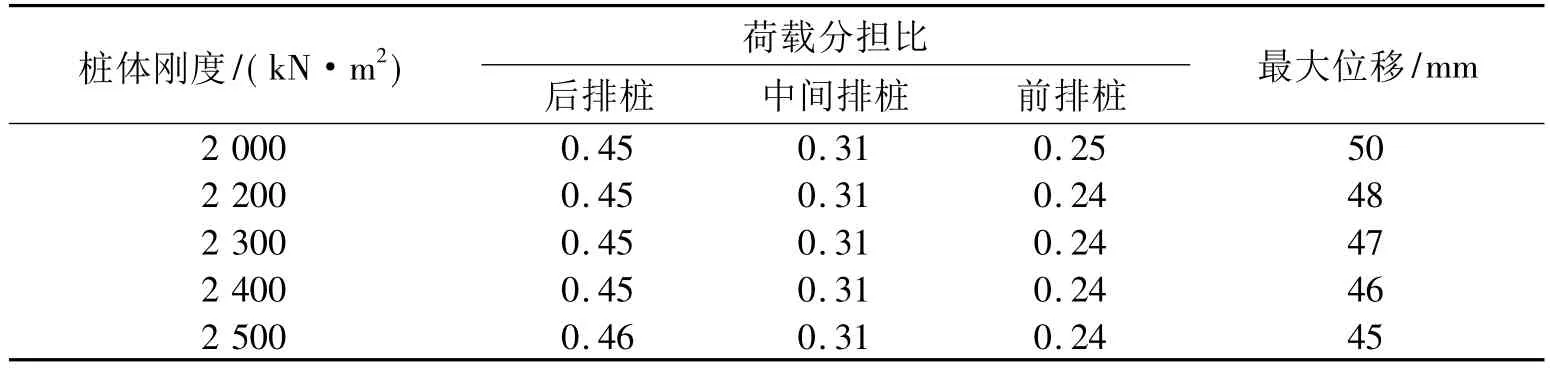
表1 桩体刚度变化对比分析

从表1中可以看出，随着钢管桩刚度的增加，后排桩承担的荷载分担比有所增加，而前排桩承担的荷载分担比则有所减小，但这种变化并不是很大，桩体刚度增加了30%，荷载分担比只变化了2.4%，中间排桩承担的荷载几乎不发生变化。所以增加桩体刚度对于各排桩之间的协同工作是不利的，但这种不利的影响非常小。钢管刚度对限制位移的发展起到了一定的影响，刚度越大，位移越小。当刚度增加30%时，位移减小了10.8%。

3.2 桩间土体压缩性

k值变化对比分析列于表2。由计算结果可以看出，随着k值的增大，也就是土体变形模量的增大，后排桩承担的荷载在减小，而中间排桩和前排桩承担的荷载在增大，荷载分担比趋于更加均匀。后排桩的最大弯矩变小，而前排桩和中间排桩的最大弯矩在增大，总体最大弯矩在减小。这表明，改善桩间土的压缩性可以使各排桩之间更好的协同工作，滑坡推力在各排桩之间的分配更加合理，最大弯矩减小。但是，当变形模量增大到一定程度后，这些变化趋于缓慢。实际工程中，通过注浆可以有效的改变桩间土体的压缩性，进而改善排桩的工作性能。

3.3 受荷段桩长

桩长变化对比分析如表3。从表3可以看出，桩的长度对于桩顶位移有着显著的影响，长度越长，位移越大。当桩的长度从6.5 m变化到7.5 m时，增加了15.4%，而桩顶位移从34.9 mm增大到了61.9 mm，增加了77.4%。由此可以看出，桩长对于桩顶位移起到了非常重要的作用。但从计算结果还可以看出，增加桩长可以使荷载分担比更加合理，各排桩之间的协同工作更加有利，但这种影响是非常微小的。所以，对于以控制桩顶位移为主的工程，应把排桩布置在滑体较薄的地方，以减小受荷段长度。

表2 k值变化对比分析

表3 桩长变化对比分析

4 结语

(1)根据小直径钢管排桩的受力特点作出合理的假设，提出了桩-土-桩相互作用的力学模型，基于Winkler弹性地基梁理论推出了排桩桩身内力及位移的计算公式，将本文计算结果与堆载试验结果进行了对比，吻合较好，验证了本文力学计算模型及计算方法的正确性。

(2)通过讨论小直径钢管排桩桩间距、桩间土体的压缩性及受荷段桩长对其加固边坡能力的影响，得出以下结论:钢管刚度对限制位移的发展起到了一定的影响，刚度越大，位移越小;随着土体变形模量的增大，荷载分担比趋于均匀，排桩结构体系的最大弯矩减小;增长桩长可以使荷载分担比趋于合理，有利于各排桩相互协同工作，但对桩顶位移的影响较大。以上结论为计算理论的发展及工程设计提供了较好的参考依据。

［1］刘永明.小直径钢管排桩抗滑机理分析及计算理论［D］.成都:西南交通大学土工工程学院，2008.

［2］曾宪斌，林思波，黄鹏.小口径钢管桩与固结灌浆技术在岩溶地基处理中的联合应用［J］.岩土工程界，2008，12(7):36-38.

［3］张勇，盛宏光，赵红玲，等.应用钢管微型桩对倾斜楼房进行纠偏加固［J］.岩石力学与工程学报，2008，27(s1):3122-3126.

［4］Amhest Mass，Coyne A G，Canou J.Model Tests of Micro-pile Networks Applied to Slope Stabilization［C］//Proceedings of the 14th International Conference on Soil Mechanics and Foundation Engineering.Balkema:International Conference on soil Mechanics and Foundation Engineering，1997:1223-1226.

［5］冯君，周德培，江南，等.微型桩体系加固顺层岩质边坡的内力计算模式［J］.岩石力学与工程学报，2006，25(2):284-288.

［6］戴自航.抗滑桩滑坡推力和桩前滑体抗力分布规律的研究［J］.岩石力学与工程学报，2002，21(4):517-521.

［7］郑刚，李欣，刘畅，等.考虑桩土相互作用的双排桩分析［J］.建筑工程学报，2004，25(1):99-106.

［8］赵尚毅，郑颖人，李安洪，等.多排埋入式抗滑桩在武隆县政府滑坡中的应用［J］.岩土力学，2009，30(S):160-164.