基于灰色反馈模型的电力系统中长期负荷预测

张强，石振琴，李晓宇，姜秀琴

(1.内蒙古电力(集团)有限责任公司，内蒙古 呼和浩特 010020;2.内蒙古华电辉腾锡勒风力发电有限公司，内蒙古 呼和浩特 010020)

1 引言

提高中长期电力负荷预测的精度有利于制定合理的电源与电网规划、增容和改建方案，提高电力系统的经济效益和社会效益。在电力市场条件下，影响负荷的外界因素具有未知性和不确定性，因此可以将负荷变量看作是在一定范围内变化的灰色量，通过数据处理将杂乱无章的原始数据整理成规律性较强的生成数列进行研究，寻求规律。灰色预测因其具有所需历史数据少，不考虑数据分布规律和变化趋势，运算简单方便，预测精度高，易于检验等优点，在电力系统中长期负荷预测中得到了广泛应用。

对于具体的负荷预测问题，目前尚不存在一种通用的模型，要提高预测精度，需要针对实际问题的特点选择合适的预测方法。和其他预测方法相比，灰色预测也存在一定的局限性。一方面当数据的离散程度越大即数据灰度越大，则预测精度越差;另一方面预测模型默认数据呈指数增长的规律，当预测系统发生转折性变化时预测的精度就很差。对于一个系统而言，随着时间的推移，未来的一些随机扰动将不断产生影响，导致系统灰度增大，预测值的精度减小。

文献［1］结合粗糙集理论给出了从负荷预测建模、缺失数据补全、有效数据筛选到决策规则生成、得出预测结果的完整预测过程。文献［2］利用最佳聚类F选优法，通过对相关历史数据进行加工处理，提炼出负荷变化的若干种典型模式，进而由影响负荷变化的相关因素的未来状态去判断未来负荷变化属于哪种模式，达到负荷预测的目的。文献［3］将灰色系统理论中的Verhulst模型与统计学习理论中的最小二乘支持向量机算法有机结合，融入等维新息技术，提出了用于处于饱和增长状态的中长期负荷预测灰色模型。文献［4］结合聚类分析与时间序列数据挖掘技术，提出了基于粒计算的动态聚类预测模型。文献［5］将灰色理论与Bernoulli微分方程组结合，构建了适用于不同发展趋势曲线的中长期负荷预测模型。文献［6］在最大限度保留原有数据信息的前提下，将数据信息集中在几个互不相关的主成分上，通过偏最小二乘回归分析实现电力负荷的中长期预测。文献［7］提出了基于椭圆图的异常数据识别和基于最小二乘支持向量机的缺失数据填补方法，为提高中长期负荷预测精度提供了有力的支持。文献［8］通过历史典型日负荷数据构建出典型日年度发展时间序列，通过支持向量机方法对预测日各时段负荷值进行预测。文献［9］通过对原始数据序列进行开次方运算生成新数据序列，建立改进后的无偏灰色模型，取得了满意的结果。本文在经典GM(1，1)模型的基础上，提出利用对数函数－幂函数变换数据，减小了原始数据的增长率，采用等维新息方法处理历史数据降低了负荷发展系数。首先通过处理后的数据建立GM(1，1)模型，直接求解时间序列;再以时间序列作为反馈信息建立灰色反馈预测模型，得出预测值即为最终的负荷值预测结果。最后利用该模型，对两个算例进行了分析，得到了满意的效果。

2 对数函数－幂函数变换处理数据的有效性

用幂函数变换和对数变换都可以增加数据的光滑度，从而提高预测精度［10，11］。现将这两种变换进行复合变换，即先用对数变换处理原始数据得［lnx(0)(r)］，然后再用幂函数变换处理数据列［lnx(0)(r)］得{［lnx(0)(r)］1/T}(T≥1)，然后利用建立灰色反馈 GM(1，1)模型进行预测，最后通过exp{［^x(0)(r)］1/T}T还原数据，得出最终结果。先给出三个定理(定理证明见文献［10］)，以便更好的理解对数函数－幂函数变换处理数据的方法。

定理1:若x(k)为递增数列，且x(1)≥1，T≥1则:

定理2:若x(k)为递增数列，且x(1)≥e则:

定理3:若x(k)为递增数列，且x(1)≥e，T≥1则:

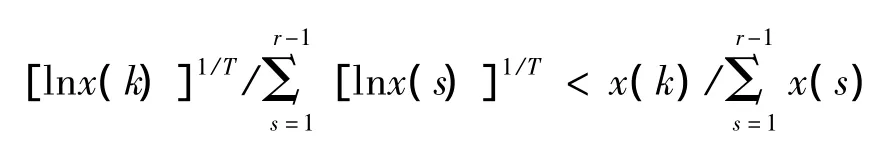
由上述定理知，对数函数变换、幂函数变换均可提高数据的光滑度，而且它们的复合变换效果更佳。

3 灰色反馈预测模型的建立和求解

步骤一:将已知数据样本集:

按照时间的顺序依次划分成互不相交的两个子集:

将BS的数据变换为:

利用变换后的数据建立 GM(1，1)模型［12－14］，得:

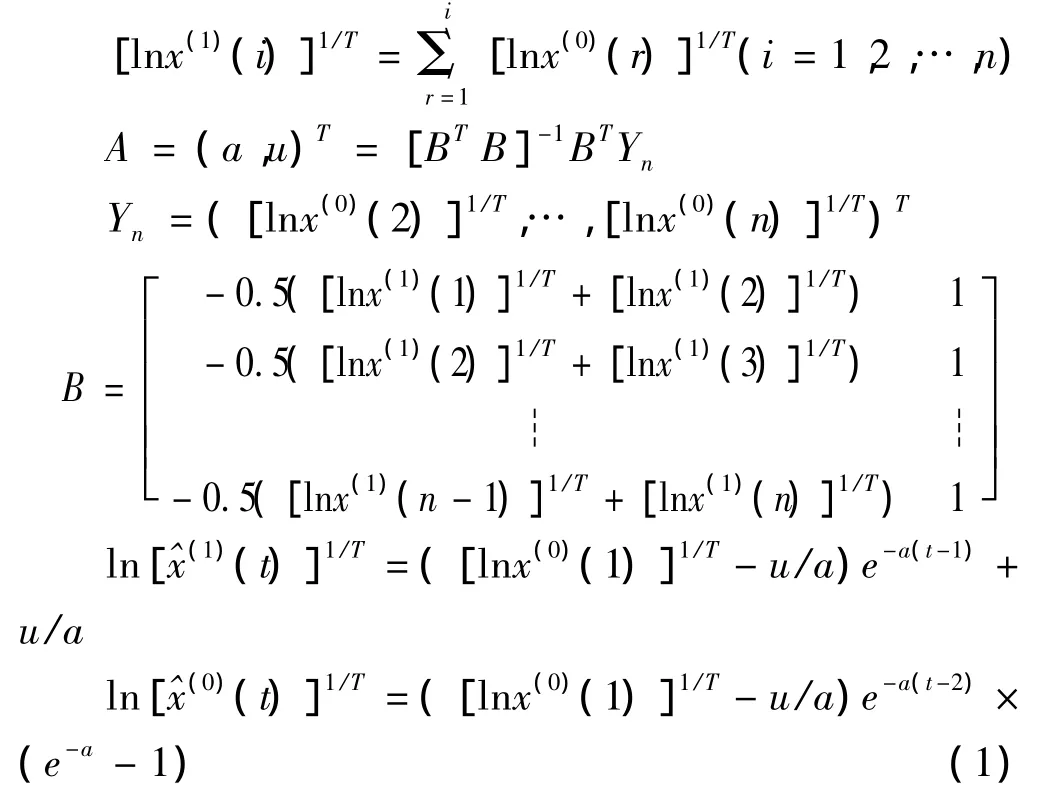
步骤二:由公式(1)解出t:

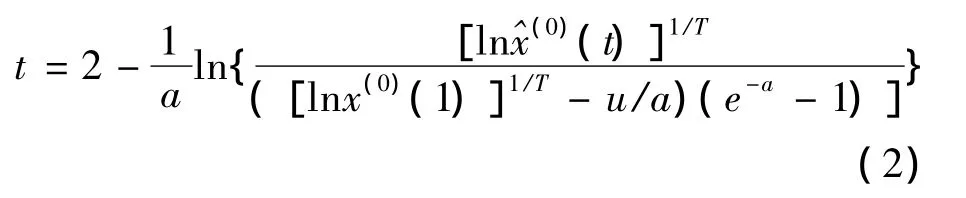
将数据样本集AS中的数据逐一代人公式(2)中取代(0)(t)求出t值，得出新的t值序列t(0)。t(0)=［t(0)(1)，t(0)(2)，…，t(0)(n)，t(0)(n+1)，…，t(0)(r)］。

步骤三:利用t(0)的数据建立GM(1，1)模型，得出:

令S=1，2，…，n，n+1，…，r，r+1(r+1 为预测序号)，求出t的预测值序列(0)，

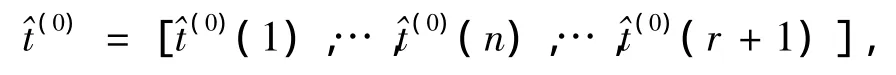
把(0)代入式(4)(代替公式中的t):

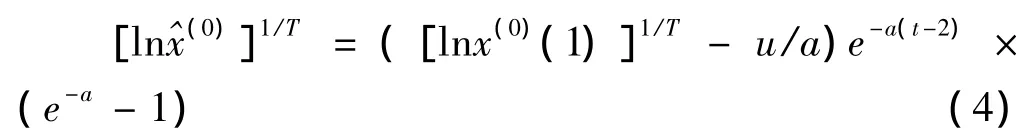
得到预测值序列［ln(0)］1/T:

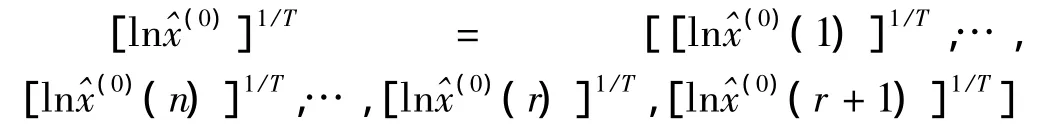
步骤四:利用exp{［ln(0)］1/T}T还原预测值序列［ln(0)］1/T，出最终结果。

步骤五:利用预测值(0)(r+1)作为一个新的已知数，置于原数据列最后一位之后，同时去掉原数据中的x(0)(1)，以保持数据相同的维数，重复以上步骤，直至预测到所要求的年份。

4 算例分析

4.1 对5种具有代表性的负荷数据进行预测

文献［15］提供了五种具有代表性的负荷模型的数据，如图1所示。其中包括三种近似指数增长规律，但增长率各不相同的负荷序列，它们模拟了处于发展初、中级阶段中小型城市的负荷增长。另一种为具有饱和特性，近似按Gompertz曲线规律增长的负荷序列，它模拟了一些发达国家大型城市的负荷增长;还有一种是近似按S型曲线规律增长的负荷序列，它模拟了城市发展初期处于快速增长阶段而后期逐渐进入饱和阶段的负荷增长情况。现利用灰色反馈模型进行预测，验证模型的有效性，结果如表1所示。从表1中可以看出，对以上五种不同增长规律的负荷序列进行预测时，灰色反馈预测模型对负荷类型1、2、3具有较强的适应性，其中负荷1的相对误差为－2.99%，负荷2的相对误差为 －1.06%，负荷3的相对误差为 －2.62%，预测精度均控制在±3%以内，满足中长期负荷预测的要求。而对于负荷类型4、5预测精度不高，其中负荷4的相对误差为－29.46%，负荷5的相对误差为－23.43%。对于按近似Gompertz曲线规律增长或者按近似S型曲线规律增长的负荷，可以采用灰色Verhulst模型进行预测。

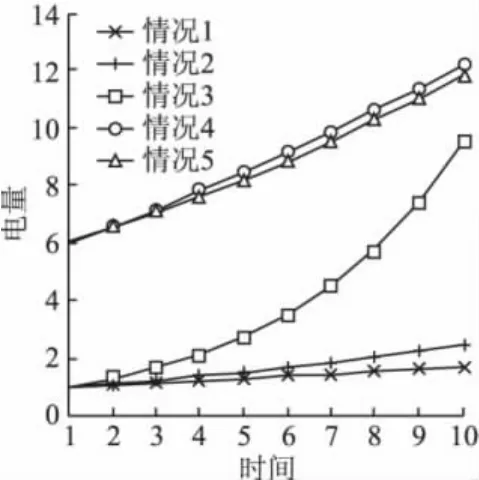
图1 不同用电量发展趋势示意图

表1 灰色反馈预测模型对5种代表性负荷的预测结果

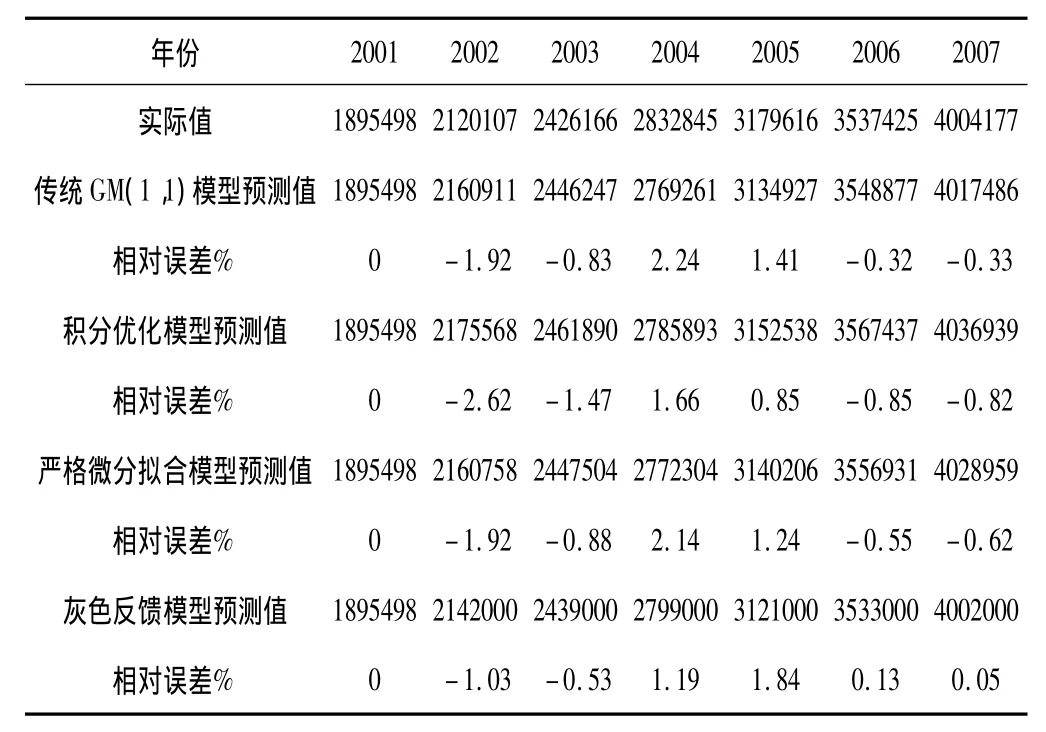
表2 几类预测方法结果比较(单位:104kWh)

表3 某地电网2008－2016年负荷预测结果(107kWh)

4.2 实际负荷预测

结合广东某地电网的历史电力负荷数据，利用对数函数－幂函数变换和等维新息处理数据建立灰色反馈预测模型进行相应的分析计算，并与传统GM(1，1)模型、积分优化模型、严格微分拟合模型进行了比较，结果如表2所示。并应用灰色反馈模型预测了该地2008～2016年的全社会售电量，预测结果见表3。

从表2中数据可以看出，灰色反馈预测模型的最大预测误差是1.84%，平均预测误差是0.8%，预测精度优于传统GM(1，1)模型、积分优化模型和严格微分拟合模型，符合中长期负荷预测要求。但灰色反馈预测模型在实际应用中还存在局限性，它比较适用于具有较强指数规律的负荷序列，而对于特殊的负荷增长方式，如当负荷按照S型曲线进行增长或增长处于饱和阶段时，若采用该灰色模型则预测误差较大，预测精度不满足实际要求，这也是下一步研究的主要工作。

5 结论

灰色反馈模型虽然要通过两次独立的经典灰色模型运算，但是灰色模型算法简单，涉及的运算少不必对数据做过多的处理，便于计算机编程实现。通过利用对数函数－幂函数变换处理历史数据，建立等维递补灰色反馈模型对近似指数规律增长的负荷(不管负荷增长率的大小)进行中长期负荷预测，不但具有较高的预测精度，而且保留了灰色理论预测方法的优势和特点，具有较强的实用性，能够更好地为电网规划规划、增容和改建提供决策依据，促进电力系统和谐发展。

［1］罗治强，张焰，朱杰.粗集理论在电力系统负荷预测中的应用［J］.电网技术，2004，28(3):29 －32.

［2］伍力，吴捷，叶军.负荷中长期预测中一种改进的模糊聚类算法［J］.电网技术，2000，24(1):36 －38.

［3］周德强.改进的灰色Verhulst模型在中长期负荷预测中的应用［J］.电网技术，2009，33(18):124 －127.

［4］顾洁，杨熠娟，施伟国.基于粒计算的电力系统中长期负荷动态聚类预测模型［J］.电网技术，2009，33(20):120 －124.

［5］方仍存，周建中，张勇传，等.基于粒子群优化的非线性灰色Bernoulli模型在中长期负荷预测中的应用［J］.电网技术，2008，32(12):60－63.

［6］毛李帆，江岳春，龙瑞华，等.基于偏最小二乘回归分析的中长期电力负荷预测［J］.电网技术，2008，32(19):71 －77.

［7］毛李帆，姚建刚，金永顺，等.中长期负荷预测的异常数据辨识与缺失数据处理［J］.电网技术，2010，34(7):148 －153.

［8］蔡国伟，杜毅，李春山，等.基于支持向量机的中长期日负荷曲线预测［J］.电网技术，2006，30(23):56 －60.

［9］郑文琛，吉培荣，罗贤举.改进无偏GM(1，1)模型及其在中长期电力负荷预测中的应用［J］.继电器，2008，36(5):36－39，44.

［10］李群.灰色预测模型的进一步拓广［J］.系统工程理论与实践，1993，13(1):64 －66.

［11］何斌，孟清.灰色预测模型的拓广方法研究［J］.系统工程理论与实践，2002，22(9):137 －140.

［12］曹国剑，黄纯，隆辉，等.基于GM(1，1)改进模型的电网负荷预测［J］.电网技术，2004，28(13):50 －53.

［13］张伏生，刘芳，赵文斌，等.灰色Verhulst模型在中长期负荷预测中的应用［J］.电网技术，2003，27(5):37 －39，81.

［14］邓聚龙.灰色预测与决策［M］.武汉:华中理工大学出版社，1986:10－15.

［15］王成山，杨军，张崇见.灰色系统理论在城市年用电量预测中的应用－不同预测方法的分析比较［J］.电网技术，1999，23(2):15－18.