基于ANSOFT的含气隙铁心线圈电感分析
李卫国,芦竹茂,叶高生
(华北电力大学高电压与电磁兼容北京市重点实验室,北京 102206)
1 引言
电力系统中存在大量含铁心线圈的非线性电感元件,如变压器的励磁支路、电抗器、电磁式电压互感器等。但现有文献只是通过数值方法进行电感分析,这些方法都比较复杂、繁琐有一定的局限性。尤其是在计算发生故障后可能出现的短路电流使得铁心材料出现磁饱和而引起的电感变化[1-4]。
本文利用铁心线圈作为切入点,采用ANSOFT软件[5,6]构建铁心线圈模型,研究线圈磁饱和后引起的电感变化,并深入研究了当磁环内部存在的气隙对线圈电感影响。由于铁心饱和会导致电感非线性变化,因此,仿真结果对于制造较稳定的电感输出设备有一定的指导作用。
2 仿真模型的构建
基于ANSOFT软件的MAXWELL3D电磁场仿真步骤为:建立几何模型、设定材料属性、指定边界条件和激励源、设定求解选项、数值计算分析和后处理等,具体流程图如图1所示。图2为构建的铁心线圈模型。
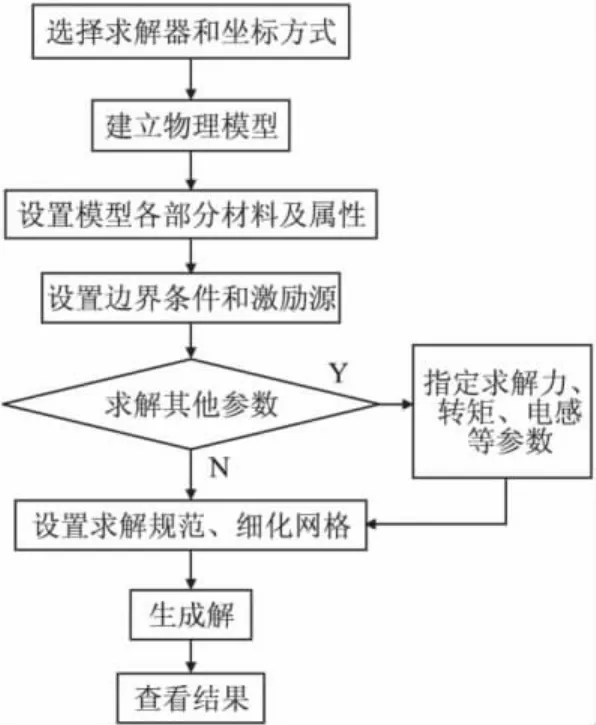
图1 Maxwell 3D建模流程图

图2 磁环仿真模型
图中黑色部分是内、外侧有一定弧度的铁心,尺寸为内径5cm、外径10cm、厚度1cm;且铁心材料的BH曲线如图3所示。左侧浅灰色部分代表线圈,绕制匝数为2000匝,厚度为0.2mm;虚线显示的是ansoft仿真施加励磁电流所需的激励面。

图3 铁心的B-H曲线
同时为了对比有、无铁心和铁心内部含不同气隙的情况,笔者做了如下的几个模型,为了便于观看以线框图的形式画出,如图4~9所示。分别表示没有铁心;铁心完好;铁心内含1mm宽度的气隙且位于线圈的中部;铁心内含1mm宽度的气隙且在与线圈上边缘成30°角的位置;铁心内含2mm宽度的气隙且位于线圈的中部;铁心内含2mm宽度的气隙且在与线圈上边缘成30°角的位置。

图4 无铁心

图5 完好铁心

图6 1mm气隙(线圈中部)

图7 1mm气隙(线圈外部)

图8 2mm气隙(线圈中部)

图9 2mm气隙(线圈外部)
3 仿真结果与分析
在利用有限元法进行三维静磁场计算电感过程中,为了计算电感矩阵,将进行一系列的磁场分析,对于n个导体组成的系统,将进行n次模拟,两个导体间耦合的磁场能为[7]:

式中,Uij是导体i和j间的磁场储能;I是导体i中的电流;Bi是导体i中施加1A电流时产生的磁通密度;Hi是导体中施加1A电流时所产生的磁场强度。
由上式可以推导出,导体之间的电感为:

由于导体由多匝线圈绕成,电感矩阵则为:

式中,N为导体的匝数。利用上述的方法对第一节介绍的6种磁环模型,仿真铁心线圈的电感L随励磁电流I(0~0.5A,步长为0.05A)的变化情况。计算结果如表1所示。需要指出的是仿真模型建立时设置线圈匝数为2000,因此,在仿真过程中施加的激励电流为:单根导线电流×2000。为了更好直观的分析各种情况下线圈的电感随电流变化情况,将表1的结果绘制成图10。

表1 6种线圈在不同电流下电感仿真结果

图10 6种线圈电感随电流变化曲线
图中分别用不同颜色对不同线圈模型仿真结果进行区分,其中黑色是没有铁心情况;红色为铁心完好的情况;蓝色为铁心含1mm宽度的气隙且在与线圈一侧成30°角的位置;紫色为铁心含2mm宽度的气隙且在与线圈一侧成30°角的位置;绿色为铁心含1mm宽度的气隙且位于线圈的中部;浅黄色铁心含2mm宽度的气隙且位于线圈的中部。
从图10可以很清晰的看出线圈在没有铁心的情况下,电感值保持不变为10.3mH,这主要是由于空气的磁导率为常数。而在有铁心的情况下,电感值要比无铁心时增加20~30倍;在励磁电流在0~300A的范围内变化时,电感值基本保持不变,这是因为当励磁电流较小时铁心没有发生磁饱和;但随着励磁电流的增加线圈的电感出现先增加后减小,这是由于铁心出现磁饱和后电感值随电导率的变化引起的。当铁心内含气隙时,电感变化率明显小于无气隙情况;且气隙的位置和宽度也会影响电感的变化率:气隙位于线圈内部时的电感变化率要小于位于线圈外部,气隙宽度越大电感变化率越小。因此,在制造电感设备时,为了避免因短时过电流而引起的电感变化过大,可以考虑使用非全封闭式铁心,且气隙的位置和宽度要根据实际运行情况而定。
4 结语
本文利用ANSOFT有限元分析软件构建了多种情况的铁心线圈模型,分析了外施电流对线圈电感的影响。研究结果表明:铁心会大大增加线圈的电感,但随着励磁电流的增加线圈的电感会先增加后减小;当铁心内部含气隙时,气隙的位置和大小都会影响电感的变化率。仿真结果对于制造较稳定的电感输出设备,特别是在可能出现的短路电流引起的电感变化和铁心不是全封闭情况下有一定的指导作用,如干式铁心电抗器等。
[1]闫静,马志瀛,汤安.含铁心线圈励磁特性求取方法的探讨[J].高电压技术,2006,32(8):2519 -2524.
[2]黄晶晶,徐习东,曾平,等.电力变压器铁心的非线性磁化特性[J].高电压技术,2010,36(10):2582 -2587.
[3]尉军军,全力,彭桂雪,等.基于最小二乘支持向量机的励磁特性曲线拟合[J].电力系统保护与控制,2010,38(11):15 -17.
[4]张新刚,王泽忠,徐春丽.Preisach理论及其在铁心磁化过程建模中的应用[J].高电压技术,2005,31(9):14 -17.
[5]刘国志,赵凌志,蒋继娅.Ansoft工程电磁场有限元分析[M].北京:电子工业出版社,2005.
[6]何致远,康敏,矩形体充磁线圈有限元分析[J].系统仿真学报,2010,22(12):2813 -28.
[7]杨宪章,邹玲,樊亚东.工程电磁场[M].北京:中国电力出版社,2007.

