直接配点法对电池荷电状态的控制
刘历良,任世涛,沈润夏
(广西大学电气工程学院,广西 南宁 530004)
1 引言
混合动力汽车里面一般都是有好几个能量源是可用的,能量源的效率和寿命取决能量源的荷电状态和能量流动的路径。能量管理控制器决定这些因素以最好的表现方式从而满足负载的要求。因此,控制器在混合动力系统中至关重要,对系统效率和寿命影响起决定作用。
同时,控制器还要时刻保持目标函数如燃油消耗、操纵灵活性或是尾气排放量在系统约束条件下保持最优。而这些约束条件可以是能量变化率或储能装置中存储多少能量。
2 对混合动力汽车的电池进行建模
(1)电池的等价放电耗能模型
放电时的能量流路径和各个元件的效率如图1所示[1],pbatt>0。
定义Pfuel为由FPEC(Free-Piston Energy Converter)提供的负载所需要的能量:

图1 放电时的能量流路径,虚线表示的是电池中能量流路径

于是FPEC经过Δts传送到直流连接器(DC—link)上的能量:

当电池向直流连接器(DC—link)以功率Pbatt输出Δts,则电池存储能量的减少量为:

由于电池和DC/DC变换器存在损耗,则效率ηx小于1。电池中减少的能量在将来需由FPEC产生的能量将其充满。但充电的时间不再是Δts,而是时间段[t1,t2]。因此,电池的充电方程为:
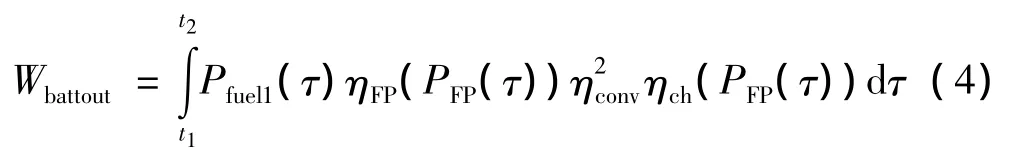
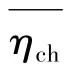

其中Wbattout是由式(3)所示。
(2)电池的等价充电耗能模型
当电池通过直流连接器充电时的能量流图如图2(Pbatt<0)[1]所示。
则Δts后,电池中增加的能量为:
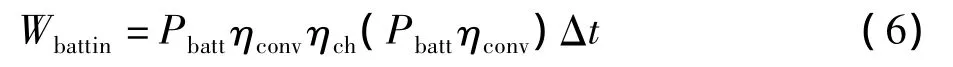
Wbattin是充入的能量,除去损耗,能够在将来某个时间里通过直流连接器(DC—link)提供Pbattout(t)能量的表达式可以表示如下:

电池在将来时刻放电效率ηdis(Pbattout(t))以一个平均值dis来近似代替,然后将式(7)重写如下:
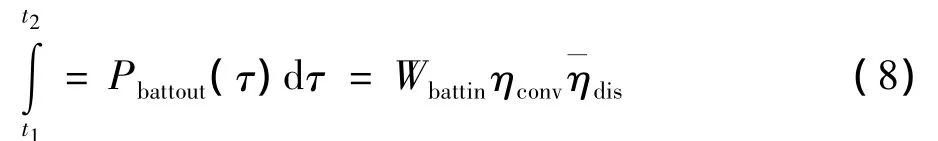
如果以上的能量完全由FPEC来提供,就存在以下的关系式:
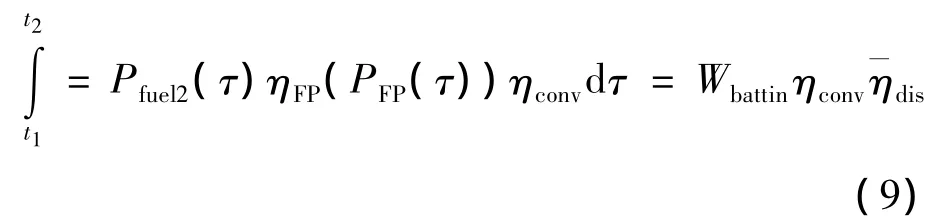
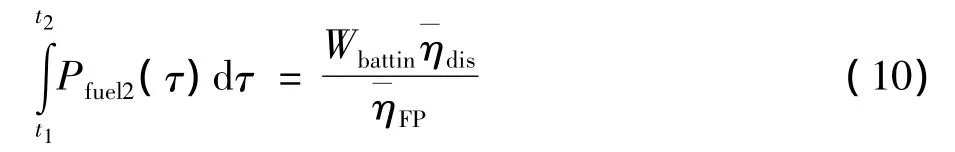
其中Wbattin由式(6)提供。
3 电池荷电状态分析
为了使电池具有高的效率和长的使用寿命,需要对电池的荷电状态控制在一定的范围内。
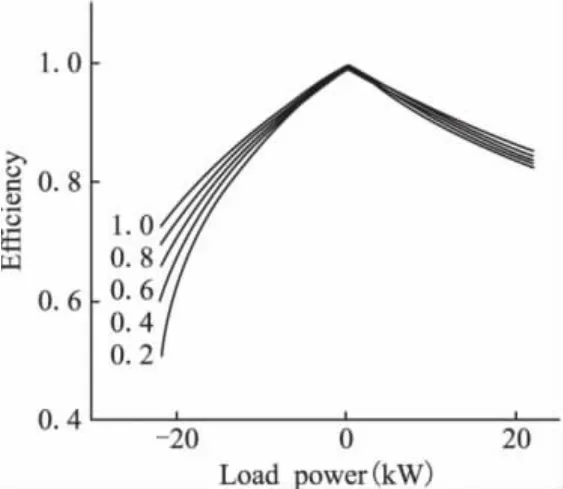
图3 不同的荷电状态值时的电池效率
图3是根据不同的荷电状态值时的电池效率图。由图可以看出,不管是充电效率或是放电效率都和荷电状态及其负载有关。并且当放电或充电达到电池极限值时或者是SOC值太小(如低于0.3)或是太高(如高于0.7)时的效率都很低,原因是此时电池本身的损耗太大。充电时,当SOC值越大时的效率相对越高,但是当SOC值较大时(如大于0.7),电池的充电效率增长不是很明显。因此,为了使电池的充电和放电效率保持在一个高的范围内,可控制SOC的值在0.3~0.7之间。
4 直接配点法优化算法
直接配点法解决最优控制问题的方法是把最优控制问题转变为非线性规划问题,即将动态优化问题转化为静态参数最优化问题,提取各个节点和配点的状态量和控制量,作为最优化参数。直接配点法与传统的间接优化法相比较,对于控制量和初始状态量的提取值不敏感,且其解具有一定的稳定性,求解的过程具有实时性等特征[2]。
直接配点法是将系统的整个时间过程平均划分成N段,每一段的左右两端点称为“节点”。在两个节点之间,用属于Gauss-Lobatto族的多项式表示连接状态变量关于时间的变化关系,并且假设控制量是线性变化的。根据多项式的不同阶次,直接配点法分为低阶的梯形法、三阶Simpson法、以及四阶、五阶Simpson法。由于直接配点法与传统的优化方法不同,直接配点法是根据实际模型的不同选择不同的方法,本文采用低阶的梯形法。
5 控制
(1)根据上面所建立的模型,得到电池的状态方程:
由式(5)得:

由式(10):


(2)控制结果如图4所示。
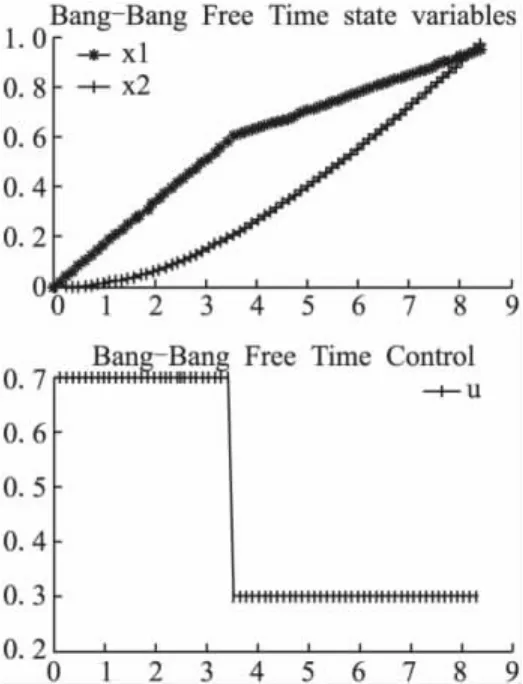
图4 直接配点法控制结果
由图4可得当电池中的荷电状态趋近于0.7时,x1是迅速增加,从而增加电池能量的输出,降低电池的荷电状态。x2的值趋于平稳;当电池的荷电状态趋近于0.3时,减小x1,从而减小电池能量的输出。同时增大x2,从而加大对电池充入的能量,使电池的荷电状态回到所期望的范围内。
6 结论
本文所建立的模型是成功的。直接配点法将混合动力汽车电池的荷电状态控制在最优的范围内,从而使电池的效率和使用寿命可以得到明显提高。方法简单,控制速度迅速,符合混合动力汽车实时快速调节的需求。
[1]Jörgen Hansson.Analysis and Control of a Hybrid Vehicle Powered by a Free-Piston Energy Converter[D].Electrical Machines and Power Electronics School of Electrical Engineering,Royal Institute of Technology(KTH)Stockholm,Sweden 2006.
[2]涂良辉,袁建平,岳晓奎,等.基于直接配点法的再入轨迹优化设计[J].西北工业大学学报,(2006)05-0653-05.
[3]Survey of Numerical Methods for Trajectory Optimization,John T.Betts,AIAA Journal of Guidance,Control and Dynamics,1998,21(2):193-207.
[4]A MATLAB Script that Demonstrates Aerospace Trajectory Optimization Using Direct Transcription and Collocation[M],The computer program solves the problem described on pages 66-69 of the classic text,Applied Optimal Control,by Arthur E.Bryson,Jr.and Yu-Chi Ho.
[5]解可新,韩健,林友联.最优化方法[M].天津大学出版社,2006.

