基于RBF的某型发动机故障诊断

秦福星 吕飞 童大鹏

（海军蚌埠士官学校机电系 安徽蚌埠 233012）

1 引言

径向基（RBF）网络是以函数逼近理论为基础构造的一类前向网络。径向基函数网络是一个只有两层的网络。在中间层，它以对局部响应的径向基函数代替传统的全局响应的激发函数。由于局部响应的特性，它对函数的逼近是最优的，而且训练过程很短。由于它具有简单的结构、快速的训练过程及与初始权值无关的优良特性，在多维曲面拟合和大型设备故障诊断等领域有着较多的应用。

2 RBF在发动机故障诊断中的应用

2.1 特征参数的选择

发动机故障的发生通常呈现出频谱分布的特点，由此，考虑将频率范围进行划分，将故障频率划分为低于1倍频部分（0.01-0.4f, 0.41-0.5f,0.51-0.99f）和1倍频、2倍频、3-5倍频等。通常，低于1倍频的频率部分主要反映齿轮、转子特性，如转子弯曲、齿轮故障、油膜涡动等；1倍频频率部分反映转子不平衡状态；2倍频频率部分对转子不对中状态等情况比较敏感；3-5倍频频率部分能反映出轴松动等情况。将上述6个频段上的谱峰能量进行归一化处理，将处理后的矢量值作为特征参数来建立故障样本数据，如表1(f为工频)所示。同时，根据现场试验和对历史数据的分析，可以采集到该型发动机发生故障时的振动信号，并将其6个频段上的不同频率的谱峰能量值归一化处理，得到表3故障样本数据。

应用上述诊断系统，对某型发动机中常出现的6种故障进行了诊断，利用6个频段上的归一化幅值作为特征参数，如表1所示。

2.2 故障模式的描述

利用0、1格式描述这6种故障模式，如表2所示。

2.3 网络的建立与训练

利用这些故障样本数据作为训练样本，创建一个诊断用RBF神经网络。

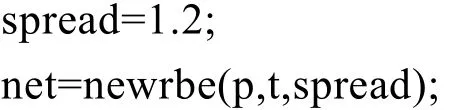
首先检验网络对训练数据的分类情况：

RBF神经网络输出结果与故障模式对应描述是一致的，表明网络可以成功将故障模式分成6类。

用表3中采集到的故障数据，检验网络的性能，程序代码为：

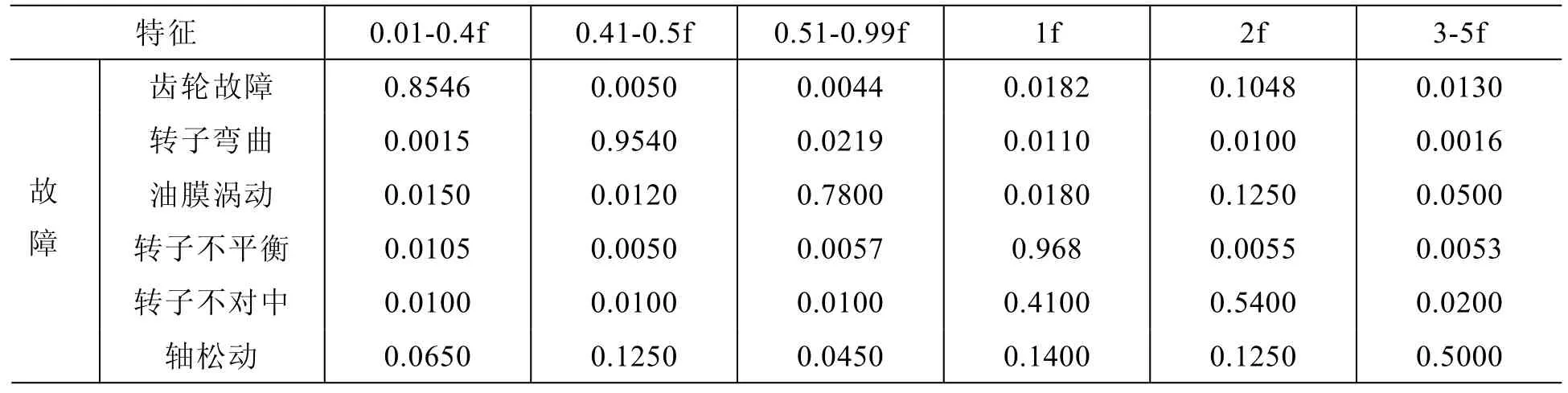
表1 故障样本数据

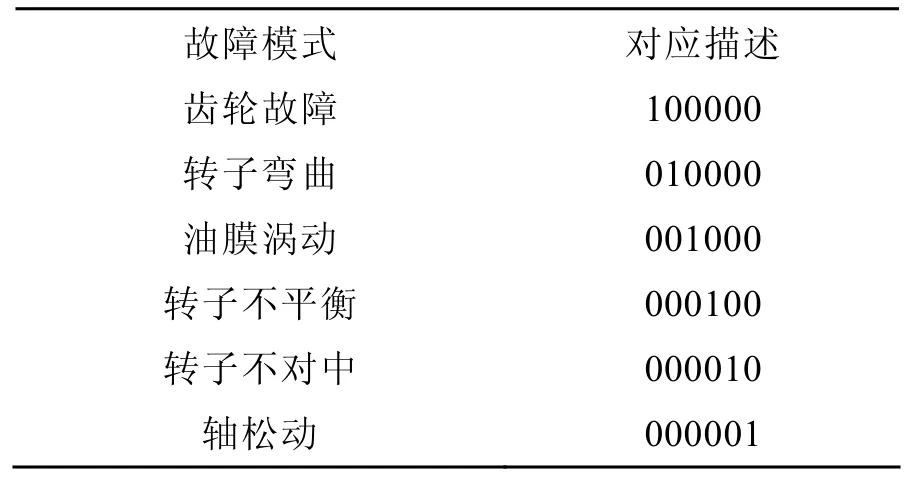
表2 故障模式分类

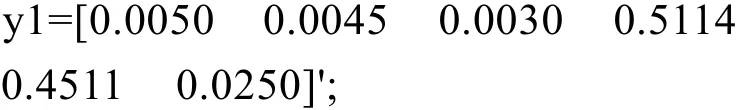
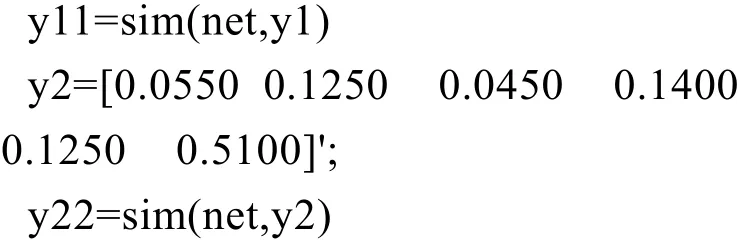
由此可见，网络用于故障诊断是正确的。

3 结论

基于 RBF的故障诊断方法可以最大限度的利用故障先验知识，在Bayes最小风险准则下进行单故障的诊断，网络训练速度快，有较高的诊断准确率。

表3 测试样本数据

[1] 张铃，张抜.人工神经网络理论及应用[M].浙江：浙江科学技术出版社，1997.

[2] neural network toolbox. mathworks，2007.

[3] 李学桥.神经网络工程应用[M].重庆：重庆大学出版社，1997.

[4] 葛哲学，孙志强.神经网络理论与MATLAB R2007实现[M].北京：电子工业出版社, 2008.

[5] 莫剑东，徐章遂，米东.RBF神经网络诊在船用低速柴油机故障诊断中的应用研究[J].华北工学院测试技术学报，2001, (1).

[6] 张定会，邵惠鹏.基于神经网络的故障诊断推理方法[J].上海交通大学学报, 1999, (8).

[7] Salama A E，Starzyk J A，Bandler J W.A unified decomposition approach for fault location in large analognetworks[J]. Intelligent Systems and Signal.Proce- ssing. 1984, 31.