基于电压电流双环解耦电压型逆变器控制的研究

庄岩，刘承志，陈勇，曹景雷，罗瑞鑫

(西南交通大学电气工程学院，四川 成都 610031)

1 引言

随着逆变器的大量实际应用，对其输出波形的要求越来越高，高质量的输出波形包括两个方面的要求:对称性和动态响应快。开环逆变器难以达到这两个方面的要求。在逆变器的闭环控制方案中，输出有效值控制方案能够维持输出有效值恒定，但不能保证电压和电流的波形质量。基于PI闭环瞬时值反馈的控制方案可以实时地调控输出电压波形，使供电质量大大提高。目前较为成熟，基于电压外环电流内环的双闭环PI控制方案是电压型逆变器的发展方向。

2 三相电压型逆变器主电路的数学模型分析

三相电压型SVPWM逆变器的主电路拓扑结构，如图1所示。

图1 三相逆变器主电路基本结构

图1中三相对称负载的逆变器主电路中滤波电感均为L，滤波电容均为C，等效电阻均为R。

2.1 三相静止坐标系下的数学模型

基于KVL和KCL定律，可得三相逆变器的电压电流方程如下:

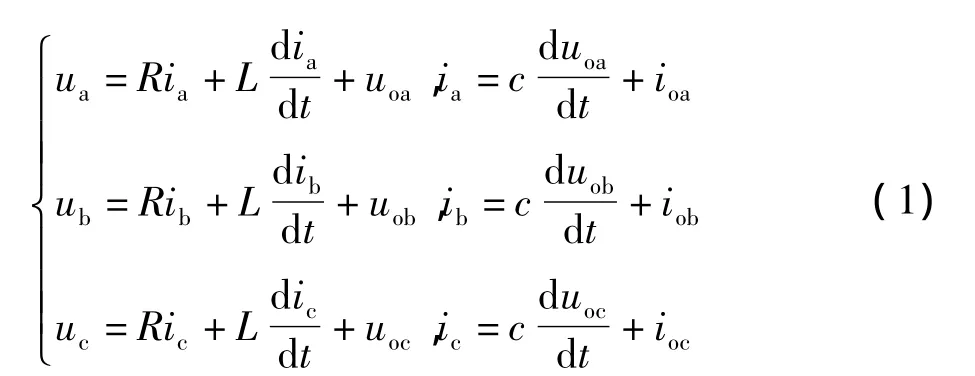
其中:ia，ib，ic是电感电流;uoa，uob，uoc是电容电压;ioa，iob，ioc是负载电流;ua，ub，uc是逆变桥输出电压。

由式(1)可得，在ABC坐标系下的模型框图，如图2所示，B，C相的模型框图得与A相相同。

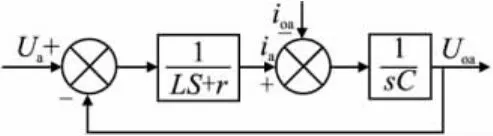
图2 三相逆变器A相的模型框图

2.2 在d－q坐标系下的数学模型

三相静止ABC(3S)坐标系到两相旋转d－q坐标系的转换矩阵为:

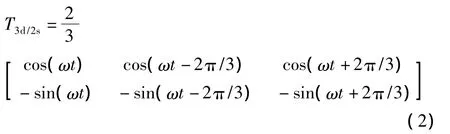
用向量图表示两者之间关系，如图3所示。

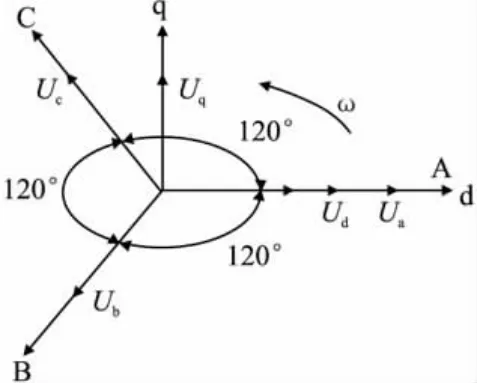
图3 三相abc/d－q旋转坐标图

因此，可得在d－q坐标系中的三相逆变器的电压电流方程为:

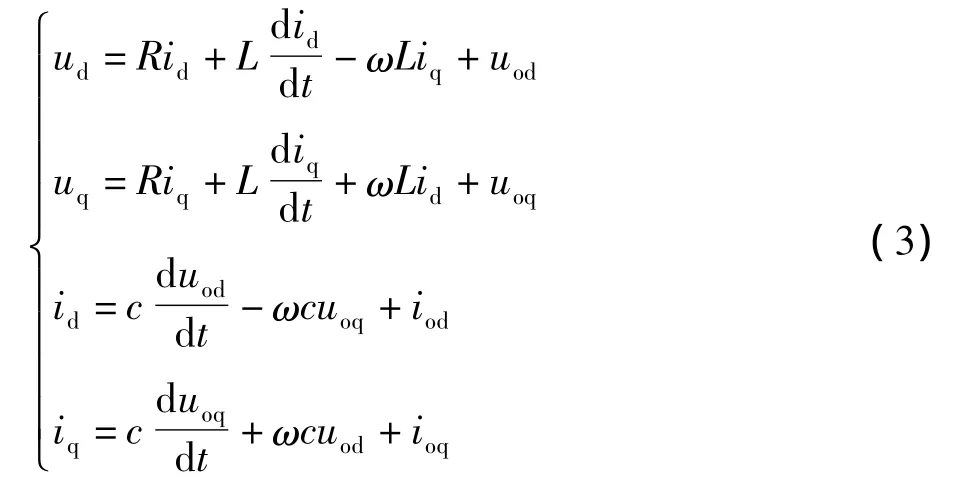
由(3)可得在同步旋转d－q坐标系下的模型框图，如图4所示。

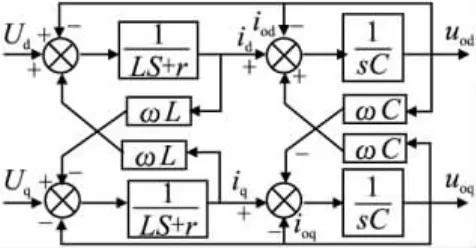
图4 三相逆变器在d－q坐标系的模型框图

电感电流电容电压的耦合，所以必须解耦。

3 电压型逆变器控制系统设计

本设计是基于电压外环和电流内环的双闭环控制器，电压外环主要作用是确定指令电流的参考值和稳定逆变器交流侧电压的幅值，通过设置q轴的电压指令为0来实现单位功率因数控制。而电流内环的主要作用是按电压外环输出的指令电流进行电流控制，内环电流控制器是实现电流的快速跟踪。

3.1 电流内环控制系统设计

电压型逆变器d－q坐标系的电流方程式:

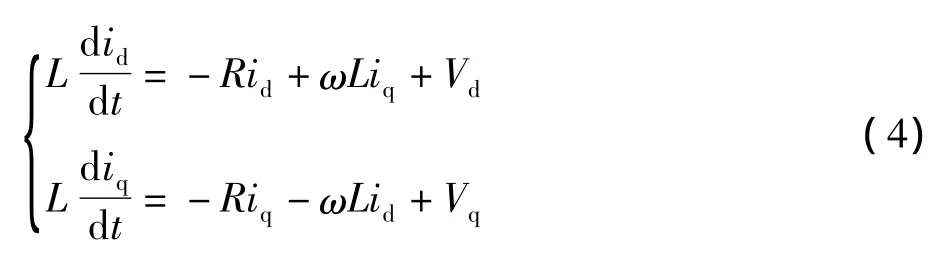
上式表明，d、q轴电流除受控制量Vd、Vq的影响外，还受到电流交叉耦合项 ωLiq、ωLid的影响。为了消除电流耦合，采用解耦控制，电流调节器采用PI调节器，则电压控制方程为:

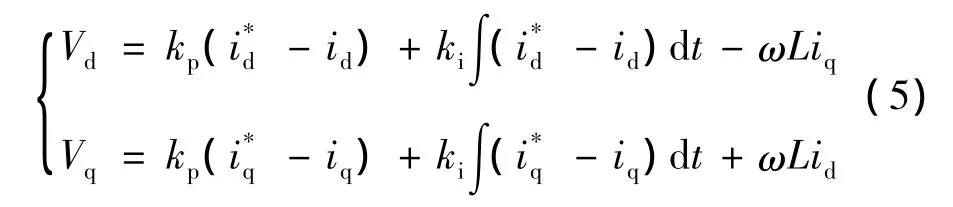
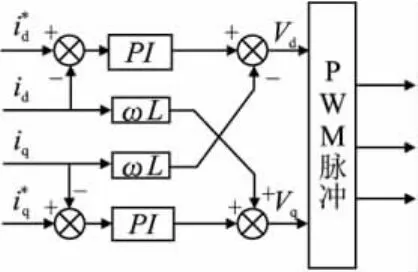
图5 内环电流解耦控制图

将式(5)代入(4)有:

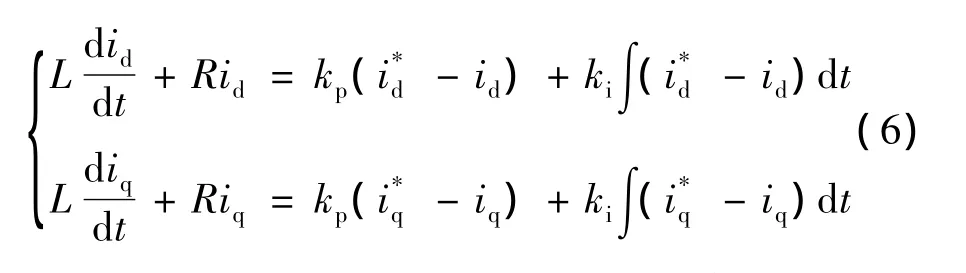
上式表明，引入电流反馈和电网电压前馈后，只要通过调节PI控制器参数使之满足式(6)，即可使id、iq分别跟踪各自参考值，产生与控制目标对应的d、q轴电流，而且实现了d、q轴电流的解耦控制。

3.2 电压外环的控制系统设计

电压外环和电流内环结构是相似的，则控制系统的设计也是相似，电压型逆变器的d－q坐标系下的电压方程方程式:

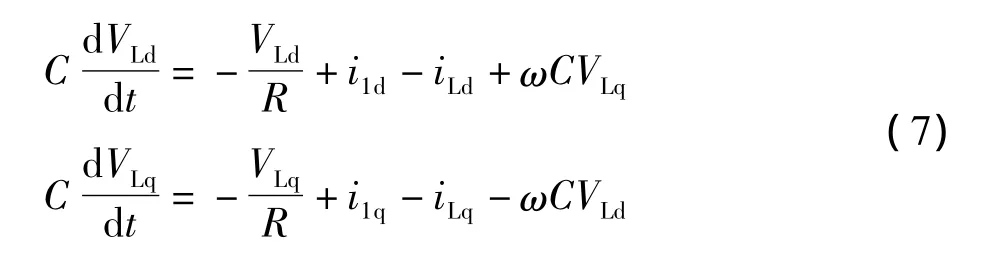
根据对电流内环的解耦控制系统研究，我们推得电压控制系统解耦方程为:

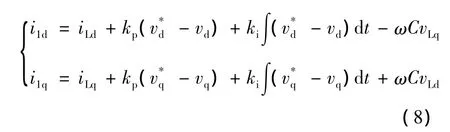
将式(8)代入(7)有:

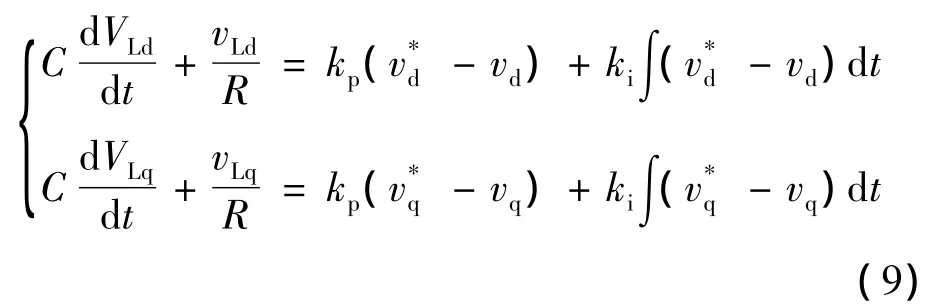
只要通过调节PI控制器参数使之满足式(8)，即可使vd、vq单独控制。

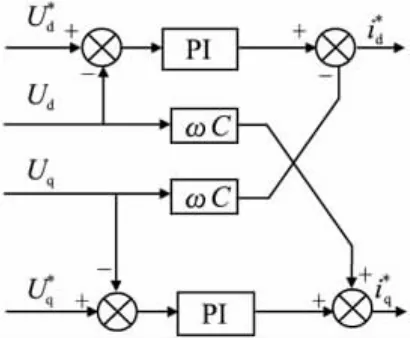
图6 外环电压解耦控制图

则根据以上分析我们可以解耦后的电压和电流的双环控制图。

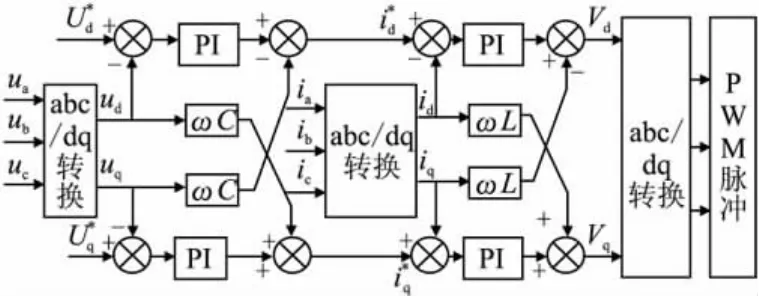
图7 双闭环控制结构框图

4 仿真验证

为了验证以上理论分析的正确性，我们应用Matlab/Simulink建立模型，仿真主电路结构如图8所示。采用电容电流内环和电感电压外环的双闭环控制对单相变三相逆变器进行仿真，直流侧电压Ud=1800V，变流器直流侧滤波电感，等效电阻RN=37Ω，稳压电容为C=1mF，负载电阻R由逆变器输入功率确定。

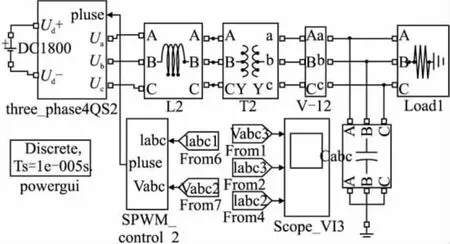
图8 单相变三相变流器仿真示意图

容性负载下的电压和电流波形，其中在容性负载下，电压滞后于电流如图9～图12。

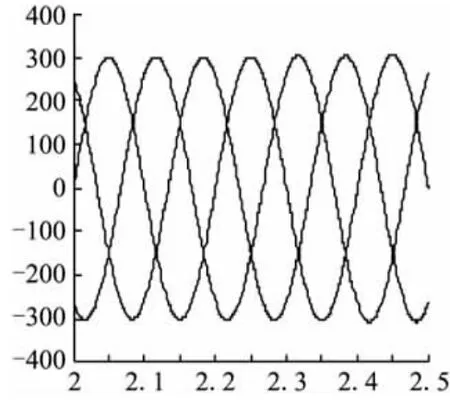
图9 容性负载下的三相对称电压波形

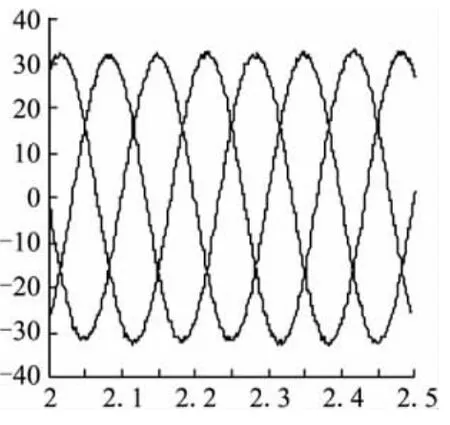
图10 容性负载下的三相对称电流波形

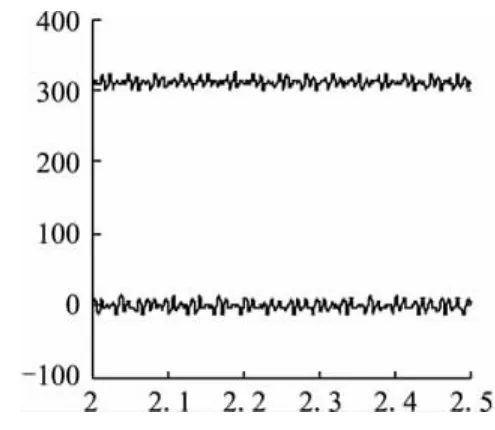
图11 电压反馈d－q变换解耦直流分量图

图12 电流反馈d－q变换解耦直流分量图

感性负载下的电压和电流波形，其中电压超前于电流如图14～图16。

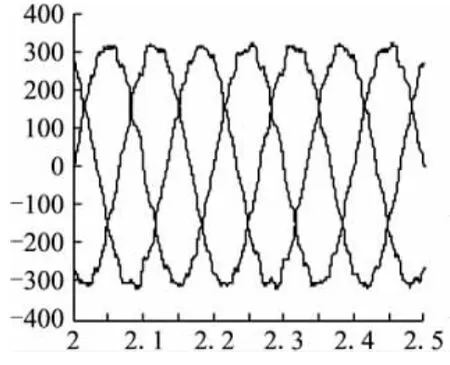
图13 感性负载下的三相对称电压波形

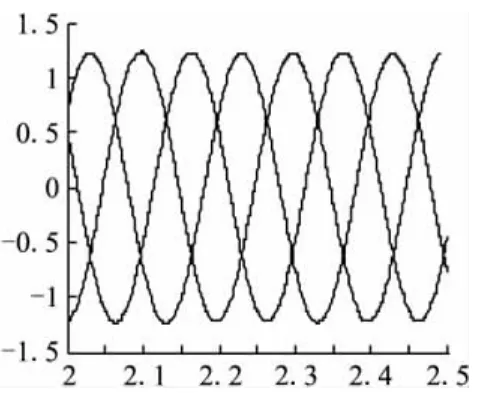
图14 感性负载下的三相对称电流波形

图15 电压d－q变换解耦直流分量图

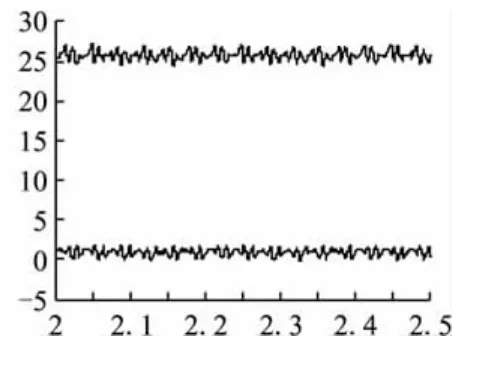
图16 电流d－q变换解耦直流分量图

5 结论

本文分析三相逆变器输出电压对称性原理，分析了三相逆变器在静止坐标系下和d－q坐标系下的数学模型，并分析了基于d－q坐标系下的电压和电流耦合关系，并利用解耦的策略和方法，采用基于PI调节器的电压和电流双闭环控制策略，并利用Matlab/Simulink建立仿真模型，分别在容性负载和感性负载下进行验证，提高了输出三相电压对称性，证明了本方法是可行的。

［1］周胜灵，丁珠玉，孙耕，等.模糊PI控制技术在逆变输出电压调节中的应用［J］.西南师范大学学报(自然科学版)，2008，33(2):1392142.

［2］白丹，蔡志凯，彭力，等.三相逆变电源不平衡负载研究［J］.电力系统自动化，2004，28(9):53257.

［3］孙驰，马伟明，鲁军勇.三相逆变器输出电压不平衡的产生机理分析及其矫正［J］.中国电机工程学报，2006，26(21):57264.

［4］毛鸿，吴兆麟.基于三相PWM变流器的无死区空间矢量调制策略［J］.中国电机工程学报，2001，21(11).

［5］张纯江，顾和荣，王宝诚，等.基于新型相位幅值控制的三相PWM整流器数学模型［J］.中国电机工程学报，2003(7):102－105.

［6］张崇巍，张兴.PWM整流器及其控制［M］.北京:机械工业出版社，2003:2－3.

［7］董晓鹏，王兆安.具有快速动态响应的单位功率因数PWM整流器［J］.西安交通大学学报，1997，31(11):77 －82.

［8］赵仁德，贺益康，刘其辉.提高PWM整流器抗负载扰动性能研究［J］.电工技术学报，2004，19(8):67 －72.