带电小球在正交场中的运动轨迹探讨

黄尚鹏

(湖北省监利县朱河中学,湖北监利 433325)

问题.如图1所示,范围足够大的磁感应强度为B的匀强磁场,方向垂直 xOy平面向里,同时在 xOy平面内充满着匀强电场,方向竖直向上,质量为 m、电荷量为 q的带正电小球从坐标原点出发,沿 x轴正方向射入场区,小球受电场力为自身重力的一半,试分析小球所有可能的运动轨迹.若小球沿轴正方向射入场区,小球的运动轨迹又是怎样的呢?

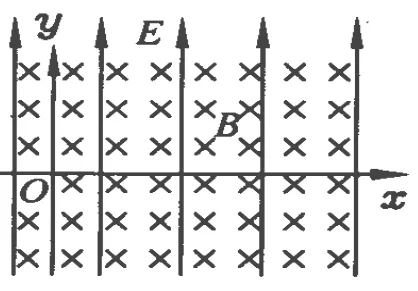
图1

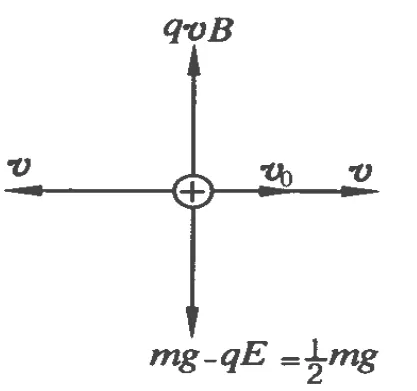
图2

若小球沿x轴正方向射入场区,如图2所示,设小球的初速度为v0,小球受电场力和重力的合力为 mg-qE=方向竖直向下,沿 x轴正方向和负方向给小球两个大小相等的辅助速度v,使 x轴正方向的速度所产生的洛伦兹力恰好与电场力和重力的合力平衡,即qvB=mg或写成v=,这样我们可以将小球的运动看成是由 x轴正方向的速度v引起的匀速直线运动和由初速度v0及x轴负方向的速度v的合速度引起的匀速圆周运动叠加而成的一种运动.为此,我们建立一以速度v沿x轴正方向做匀速直线运动的新坐标系x′O′y′,初始时刻新坐标系的原点在匀速圆周运动轨迹的圆心处,下面我们可以通过坐标变换求出小球的轨迹的参数方程.

当 0≤v0＜v时,如图 3所示,坐标系 x′O′y′中匀速圆周运动轨迹在x轴的下方,速度为 v-v0,方向为圆周运动的逆时针方向,半径 R=周期 T=角速度 ω=在坐标系 x′O′y′中小球的坐标为 x′=-Rsinω t,y′=Rcosω t,在坐标系 xOy 中小球的坐标为

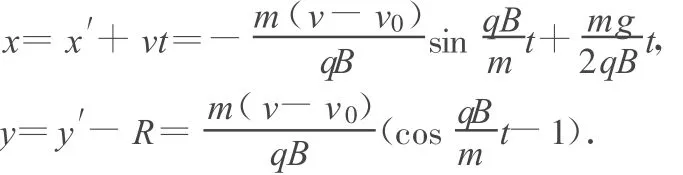
当 v0＞v时,如图 4所示,坐标系 x′O′y′中匀速圆周运动轨迹在x轴的上方,速度为 v0-v,方向为逆时针方向,圆周运动的半径 R=显然在坐标系 x′O′y′中小球的坐标为 x′=Rsinω t,y′=-Rcosω t,故在坐标系 xOy中小球的坐标为

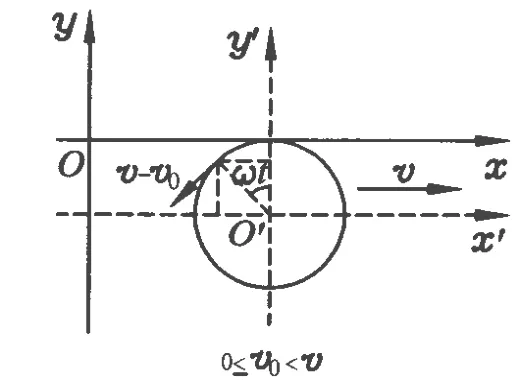
图3

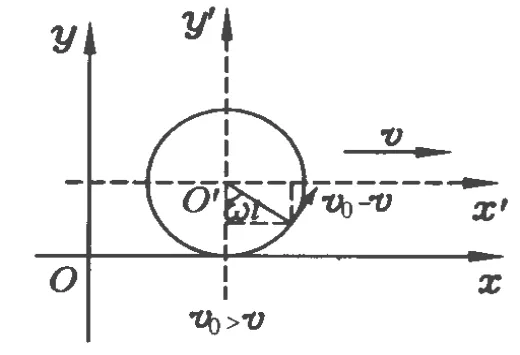
图4

显然上述两种情况下小球轨迹的参数方程形式完全相同,特殊情况下,若v0=v,则小球受洛伦兹力恰好与电场力和重力的合力平衡,小球将沿 x轴正方向做匀速直线运动.根据上述叠加思想可知,小球的运动具有周期性且从初始时刻开始每经过半个周期,小球运动的水平位移Δx=与小球的初速度 v0的大小无关.小球离开x轴的最大距离等于匀速圆周运动的直径,小球轨迹切线的斜率k=小球的速度方向沿轨迹的切线方向,下面我们分5种情况讨论小球可能的运动轨迹.

根据前面的讨论可知,小球轨迹的参数方程可统一表达为如下形式

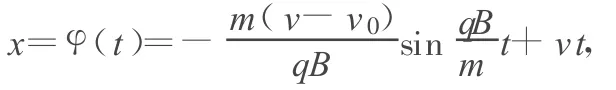
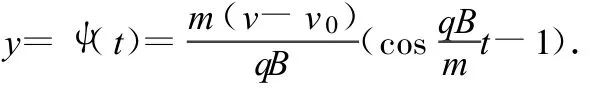
对 φ(t)和 ψ(t)求一阶及二阶导数,有

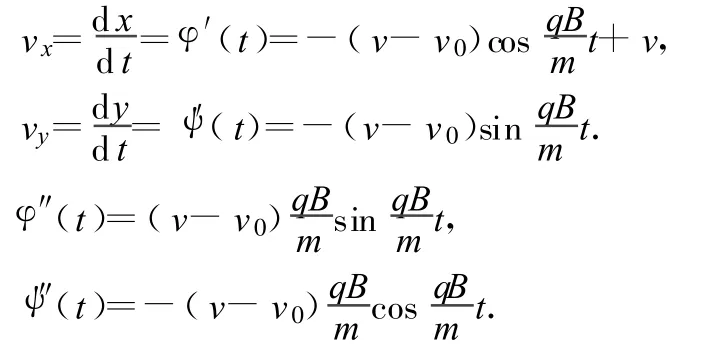
由参数方程所表示的函数的二阶导数公式可知,

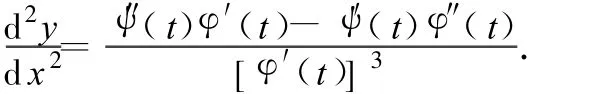
通过计算,可得

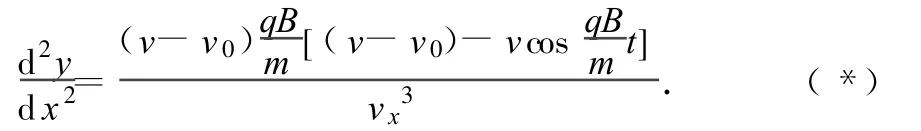
(1)当 v0=0时,由图 3可知,小球在轨迹的最低点具有最大水平速度,最低点轨迹切线水平;小球在轨迹的最高点速度为零,轨迹切线的斜率不唯一或不存在,最高点不光滑出现尖点.这种情况除轨迹的最高点外,vx＞0,函数为凹函数,轨迹向下凸.

(2)当0＜v0＜v时,由图 3可知,小球在轨迹的最低点速度水平向右,最低点轨迹切线水平;小球在轨迹的最高点也具有水平向右速度,最高点轨迹切线也水平.故这种情况轨迹可能存在拐点.

(3)当 v＜v0＜2v时,由图4可知,小球在轨迹的最低点速度水平向右,最低点轨迹切线水平;小球在轨迹的最高点也具有水平向右速度,最高点轨迹切线也水平.故这种情况轨迹也可能存在拐点.

下面给出(2)、(3)两种情况轨迹存在拐点的证明,并确定拐点的大致位置.

由高等数学知识可知,轨迹上某点是拐点的充要条件是该点的二阶导数等于零,且该点附近两侧二阶导数要改变符号.

当0＜v0＜v时,vx＞0,令得 cosω t=1显然有 0＜cosω t＜1,ω t是一、四象限的角,且由余弦函数的单调性可知,二阶导数等于零的该点附近两侧二阶导数要改变符号,故这种情况轨迹存在拐点,由图3可知,拐点在轨迹的最高点和最低点的水平中心线的上方.考虑从初始时刻开始到第1次经过最低点的过程,即0≤ω t≤π,由(*)式易知,在拐点的左侧,函数为凸函数,轨迹向上凸;在拐点的右侧函数为凹函数,轨迹向下凸.

当 v＜v0＜2v时,vx＞0,令可得 cosω t=显然有-1＜cosω t＜0,ω t是二、三象限的角,同理可知这种情况轨迹也存在拐点,由图4可知,拐点也在轨迹的最高点和最低点的水平中心线的上方.考虑从初始时刻开始到第一次经过最高点的过程,即0≤ω t≤π,由(*)式知,在拐点的左侧,函数为凹函数,轨迹向下凸;在拐点的右侧,函数为凸函数,轨迹向上凸.

(4)当 v0=2v时,由图 4可知,小球在轨迹的最低点具有最大水平速度,最低点轨迹切线水平;小球在轨迹的最高点速度为零,轨迹切线的斜率k不唯一或不存在,最高点不光滑出现尖点.这种情况除轨迹的最高点外,vx＞0,函数为凹函数,轨迹向下凸.

(5)当 v0＞2v时,由图 4可知,小球在轨迹的最低点具有最大水平向右速度,最低点轨迹切线水平;小球在轨迹的最高点具有水平向左速度,最高点轨迹切线也水平,这种情况小球在水平方向时而向右运动,时而向左运动,在轨迹的最高点下方存在水平分速度为零而竖直分速度不为零的点,在这些点轨迹的切线沿竖直方向.由(*)式知,当 vx＞0时,函数为凹函数,轨迹向下凸;当 vx＜0时函数为凸函数,轨迹向上凸.

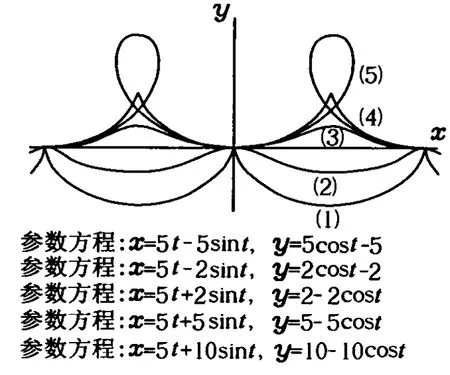
图5

采用函数作图软件SmartGraph作出的上述5种情况下小球的运动轨迹如图5所示,图中 m=1 kg,q=1 C,B=1 T,v=5 m/s.各图线代表的初速度分别为:

(1)v0=0;(2)0＜v0＜v,v0=3 m/s;(3)v＜v0＜2v,v0=7 m/s;(4)v0=2v=10 m/s;(5)v0＞2v,v0=15 m/s.注意小球的实际运动轨迹在y轴的右侧,由图5可知,轨迹的形状与上述分析是一致的.

至此,当小球沿 x轴正方向射入场区时,小球所有可能的运动轨迹都已解决,那么当小球沿y轴正方向射入场区时,小球的运动轨迹又是怎样的呢?这种情况要比上述情况要简单些,可能的轨迹形状只有一种,请看如下分析.

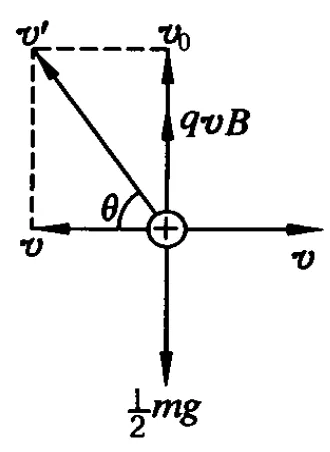
图6

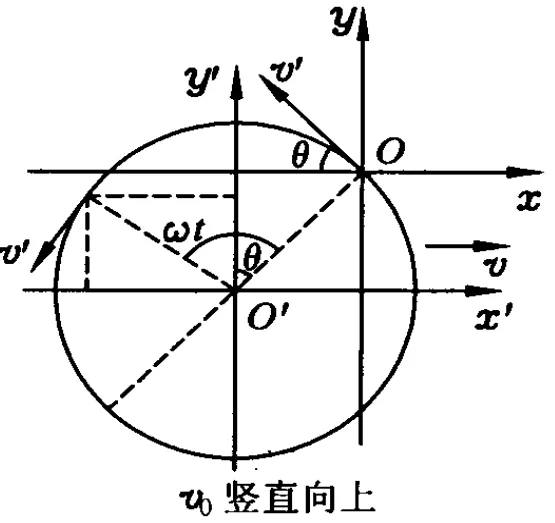
图7

若小球沿y轴正方向射入场区,如图6所示,同样将小球的运动看成是由 x轴正方向的速度v引起的匀速直线运动和由初速度v0及 x轴负方向的速度v的合速度v′引起的匀速圆周运动叠加而成的一种运动.如图7所示,坐标系 x′O′y′中匀速圆周运动的速度 v′=方向为逆时针方向,初始时刻 v′与x轴负方向的夹角为θ,且 tanθ=圆周运动的半径 R=显然在坐标系 x′O′y′中小球的坐标为 x′=-Rsin(ω t-θ),y′=Rcos(ω t-θ),故在坐标系 xOy中小球的坐标为

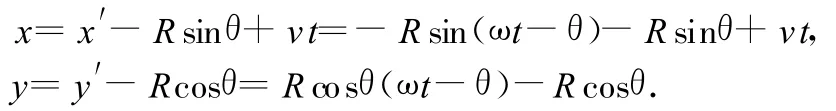
由于初速度竖直向上,故初始时刻轨迹的切线沿竖直方向,由图7可知,小球在轨迹的最高点具有水平向左速度,最高点轨迹切线水平;当小球再次回到轴时,小球的速度竖直向下,轨迹的切线沿竖直方向;小球在轨迹的最低点具有最大水平向右速度,最低点轨迹切线水平.这种情况小球在水平方向时而向左运动,时而向右运动.从初始时刻开始每经过一个周期,小球运动的水平位移为Δx=vT=与小球的初速度大小无关.

仿造前面的方法,类似可得

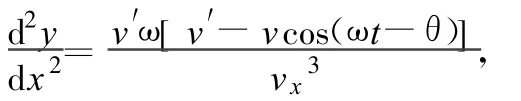
故当 vx＜0时,,函数为凸函数,轨迹向上凸;当 vx＞0时函数为凹函数,轨迹向下凸.

采用函数作图软件SmartGraph作出的这种情况下,小球的运动轨迹如图8所示,图中m=1 kg,q=1 C,B=1 T,v=5 m/s.相应的图线所对应的初速度分别为:(6)v0=5 m/s;(7)v0=12 m/s.

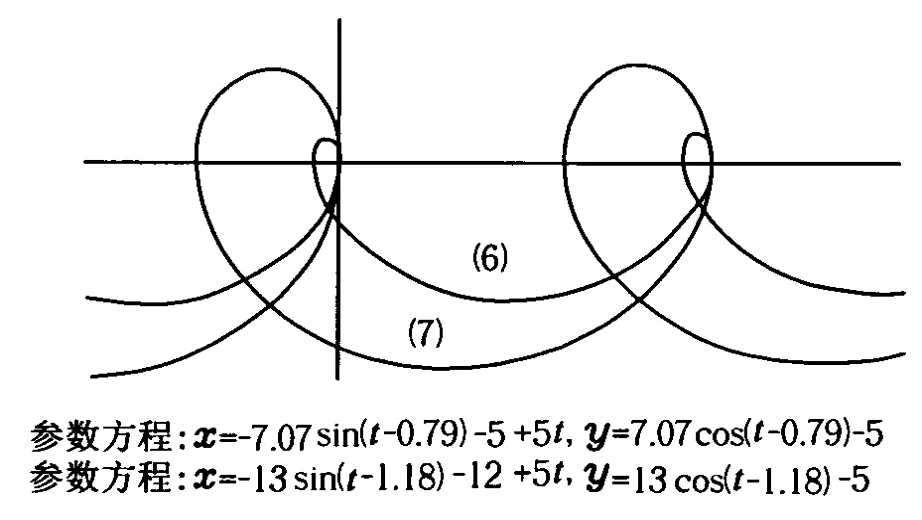
图8

编者按:带电粒子在正交场中的运动,本刊已发表了多篇文章.如无更新和更深入的意见,本刊将不再发表该类文章.