例谈变式对初中物理教学的作用

张瑞能

(无锡市洛社初级中学,江苏无锡 214187)

教育心理学家潘菽认为,“变式就是使提供给学生的各种直观材料和事例不断变换呈现的形式,以使其中的本质属性保持恒在,而非本质属性则不常出现,成为可有可无的东西.”如果在物理教学中我们能够在保持内容本质不变的前提下使其呈现形式不断发生改变,对教学内容进行灵活变式,将可以起到较好的作用.

1 有利于把握知识的本质

马登“现象图式学”理论认为,学习发生的前提是有效的分辨,学习认识事物或现象往往就是从中区分出一些主要的特征,并同时将注意力聚焦于这些特征.而有效分辨的前提是变异的存在,因此,变异构成了学习的重要前提条件.在解决问题时,将问题或问题中各个对象通过一般化、特殊化、具体化、类似化等方式进行变式,将原来问题转化归结为学生比较熟悉的另一个相关问题,再从这一相关问题的解答过程或结论中,通过归纳或迁移得到原问题的结论或者解题的启示.根据对问题解决的理解和预见,可能导向不同的变式,在这样的变式过程中,促进学生把握知识的本质.如在“滑轮”一节习题教学中,笔者设计了这样一道习题.

例1.一个轻质圆形滑轮,如图1所示,细线一端固定在地面上,另一端吊一个重物G,在轴心处用力F向上匀速拉动滑轮,不计摩擦,求F:G.

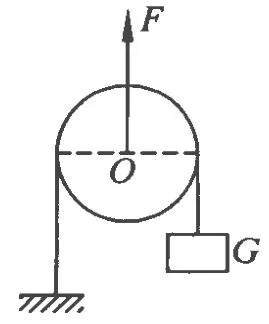
图1

图2

很显然,本题不属于学生常见的滑轮类的题目,不能通过简单地套用滑轮的特点、公式来解决.如果通过图形变式,将其变换成图2所示.

变式:椭圆形轻质薄板中间悬挂一根细线,当它在图2所示的位置平衡时,求F:G.

这个装置是不是杠杆?如果是,它的支点又在什么地方?

通过上述铺垫,可以使学生理解图1所示的装置实质仍然是个杠杆,从而进一步加深他们对滑轮本质的理解.

2 有利于拓展学生的思路

物理教学离不开解题,解题的目的是通过解题深化学生对知识的理解,提升学生的思维水平,从而积累解题经验、发展能力.在解题过程中,通过变更题目的已知条件、提问方式来引导、促进学生从不同角度思考问题,通过对解题方法分析与比较来揭示蕴涵于其中的思想方法以及各自的特点、适用范围等,拓展学生的解题思路.

例2.如图3所示,有一斜面高5 m,长25 m,机械效率为80%,要把一个重100 N的物体匀速拉到顶端,则沿斜面向上的拉力是多少?所受斜面的摩擦力为多大?

图3

以前学生求滑动摩擦力通常是根据平衡力(二力平衡或同一直线上的几个力平衡)的知识来解决的,可是本题中物体受力情况比较复杂,用平衡力的知识来解决对初中生来说,显然是比较困难的.

变式1:如果是理想机械,拉力多大?(引导学生从功的原理的角度来进行分析,因为使用任何机械都不能省功)

既然有摩擦,实际拉力必将增大,而增加的力即是克服摩擦力所需要的力,所以只要求出实际拉力,问题就基本解决了.

变式2:通过效率的本质——有用功和总功的比值,总功和额外功分别多大?

额外功就是克服摩擦力所不得不做的那部分功,这样问题就能迎刃而解了.

上述变式的基础都是建立在“斜面是一个简单机械”的前提之上,通过这样变式处理,可以使学生对斜面这一机械有更深刻的认识,也能对效率的理解更透彻,从而加强知识的链结,形成系统性的知识,提高整体的认知水平.

3 有利于形成良好的认知结构

解题过程中的变式和解题之后的变式,都是针对具体的例题、习题的,而课堂(特别是一些复习课、练习课)可能是由一系列层次递进的例题、习题串联而成的,教师往往是从某个例习题出发,通过逐步变式得到一系列问题,这就是课堂例题、习题设计中的变式.通过变式设计的例题、习题,从文字到内涵都有很多“交集”,前面的例题、习题的部分题目信息可以直接推移到后续的例题、习题中,从而可以节约学生审题时间,提高课堂容量.通过变式设计的例题、习题,还可以知道相互之间在具体背景、研究对象以及研究方法等多个方面存在着各种各样的内在联系.正因为这样,巧妙地运用变式设计例题、习题,不仅可以提高课堂容量,还有利于学生形成良好的认知结构,提高课堂教学效率.

例3.一只体积为200 cm3、质量为1 600 g的实心金属球,问该球是铜制的吗?你能帮他想出办法吗?(ρ铜=8.9×103kg/m3)

在全面复习了密度及其变形公式的情况下,进行变式:

变式1:质量不变,体积为450 cm3水结成冰后,体积为多大?(ρ冰=0.9 g/cm3)

变式2:体积不变,能盛16 kg酒精的塑料桶若用来装水,能装多少千克?

变式3:气体密度变式.一只钢瓶内的氧气密度为6 kg/m3,用去其中的后,余下的气体的密度是多少?

通过前面的例题、习题变式设计,可以帮助学生完善“密度不变、质量不变、体积不变”3种情况下密度知识的运用.最后又通过气体的密度的特殊性,可以使学生进一步理清思路,完善对这一部分知识的认识,形成良好的认知结构.

4 有利于促进学生的学习主动性

再好的教学手段、教学方式,若没有学生的积极参与都不会收到好的效果,所以,不论是什么教学模式,其根本的出发点都是要调动学生学习的主动性.根据维果茨基的“最近发展区”理论,变式教学就是根据学生的现有知识水平,通过恰当的变式,变换同类问题的非本质特征,让问题处于学生的“最近发展区”,使他们学习的积极性得到最大程度的激发,使问题得以解决的可能性更大,从而帮助学生达到更高的潜在水平.

例如在浮力教学时,创设这样的问题:画出在空中静止的汽球、停在水面上的轮船所受到的力的示意图.

思考:为什么浮力的方向是竖直向上的?

变式1:弹簧测力计下挂石块,然后用手去托,重力和拉力相等吗?

变式2:把石块放入水中,弹簧测力计的示数变了,重力还等于拉力吗?

这样设置,抓住了“浮力”这节课的基本立足点及学生认识的最近发展区——“平衡”,从“平衡”入手,得到向上的托力分别是空气和水施加的,方向是“竖直向上”的,再通过以手掌托石块的变式处理,既降低了难度,又能促使学生主动回忆并运用以前所学过的平衡力的知识,通过层层推进,既确定了浮力的方向,也得到了两种计算浮力的方法(漂浮时F浮=G物和称重法F浮=G物-F拉).

为了充分发挥变式在物理教学中的作用,教学过程中教师要有意无意地外显这样的变式过程与方法,让学生能清楚地知道教师是如何将问题逐步变化过来的,各个变式之间是什么关系.在教学过程中设置一些过渡性的语言,如“还能求什么”、“如果没有这个条件”、“条件改一下,结果将如何”等,把变式的过程以生动的方式展示出来.同时,专门安排习题课,以某一问题为出发点,展开变式,在此过程中明确变式的常用方法,如特殊化、一般化、同条件变换、逆向思考等.

因此,教师有必要加强对学生变式的督促,逐步将变式作为对学生的要求,平时要在一题多变、一题多解等方面对学生提出要求,让学生逐渐把变式转化为一种习惯.