分数微分方程m点边值问题解的存在性与唯一性*

王金华，赵育林，向红军

(1. 中山大学数学与计算科学学院，广东 广州 510275；2. 湘南学院数学系，湖南 郴州 423000)

近年来, 由于分数微积分理论的广泛发展及这些理论在许多领域的广泛应用(见文献[1-4]及其所引文献), 分数微分方程越来越受到学者们的关注, 出现了许多关于分数微分方程解的存在性和唯一性的结果, 而这些结果大部分集中在分数微分方程的初值问题的解。最近也较多地出现了一些关于分数微分方程的边值问题的文献[4-12], 但由于研究的难度较大, 较多的是两点边值问题, 而且主要是零边值条件；分数微分方程的多点非零边值问题文献很少见。其中，文[5]考虑了如下m点边值问题

文[6]研究了以下非局部多点边值问题

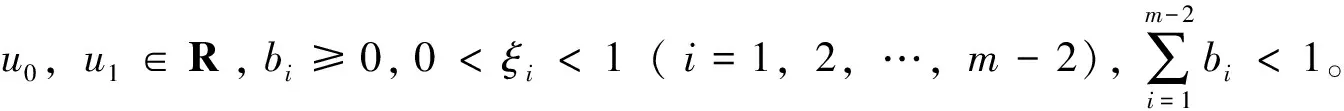
本文考虑如下m点边值问题

(1)

1 准备工作

在这一节里，先给出本文所涉及的一些分数阶导数，分数积分的定义和一些基本命题。

定义1[1-2]函数y:(0,∞)→R的α>0 次的Riemann-Liouville分数积分为

上式右端在内(0,∞)内逐点有定义。

定义2[1-2]函数y:(0,∞)→R的α阶Caputo分数导数为

其中Γ是gamma函数,n=[α]+1，[α]表示α的整数部分, 上式右端在(0,∞)内逐点有定义。

注1 当α→n时, 上式中的Caputo导数即为函数y(t)的经典的n阶导数。

定义3[5]函数x(t)的α(α∈(n-1,n],n∈N)阶Pseudo分数导数为

引理1[7](Schauder不动点定理) 设U是Banach 空间X的有界闭凸子集，如果T:U→U是全连续算子，则T在U中有不动点。

由Caputo分数导数的定义及注1，可以得到如下结论。

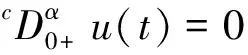
u(t)=c0+c1t+c2t2+…+cn-1tn-1

其中，ci∈R，i=0,1,…,n-1，n=[α]+1。

由以上引理2, 有如下引理。

引理4 设y∈C[0,1], 则边值问题：

(2)

(3)

有唯一解

证明将 (2)式 两边求α次积分，由引理3得

(4)

将上式两边求导得

(5)

将c0,c1代入(4)式得

2 主要结果

利用Banach及Schauder 不动点定理分别讨论系统(1)解的存在性及唯一性。

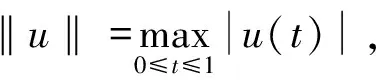
另定义算子T:X→X如下

(6)

定理1 假设以下条件成立

(i) 函数f:[0,1]×R→R连续；

(ii) 存在正的常数L*>0使得函数f(t,u(t))满足

|f(t,u)-f(t,v)|≤L*|u-v|,

t∈[0,1],u,v∈R

则分数边值问题(1)在区间[0,1]上有唯一解。

证明由引理4及(6)式可知，只需证明(6)式所定义的算子T有唯一不动点即可。设∀u(t),v(t)∈X, 则对∀t∈[0,1]，有

|f(s,u(s))-f(s,v(s))|ds+

|f(s,u(s))-f(s,v(s))|ds+

|f(s,u(s))-f(s,v(s))|ds≤

L*‖u-v‖<‖u-v‖

于是有‖Tu(t)-Tv(t)‖<‖u-v‖，t∈[0,1]。

因此,T:X→X是压缩映射, 由Banach不动点原理T在X中有唯一不动点。 即边值问题(1)有唯一解，证毕。

定理2 设函数f:[0,1]×R→R连续，且存在一个在[0,1]的任何子区间上都不恒等于零的非负连续函数p(t)及非减函数φ:[0,+∞)→[0,+∞)使得

|f(t,u)|≤p(t)φ(|u|), (t,u)∈[0,1]×R

同时存在正的常数r，使得p0φ(r)≤r。则边值问题(1) 至少有一个解，这里

证明令U={u(t)∈X|‖u‖≤r,t∈[0,1]}。将用Schauder不动点定理证明T在U中至少有一个解。下面分三个步骤：

1)T:U→U。

任取u∈U，则有‖u‖≤r。于是，对∀t∈[0,1]，有

|f(s,u(s))|ds+

p0φ(r)≤r

所以有‖Tu(t)‖≤r，即T:U→U。

2)T连续的。

设{un(t)}是X中的函数列且un(t)→u(t)∈X，t∈[0,1]。由于

而f(t,u(t))连续，因此当n→+∞时，有|Tun(t)-Tu(t)|→0。所以T:U→U连续。

3)T是等度连续的。

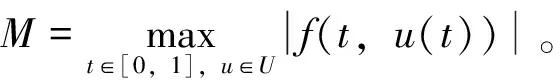
|Tu(t2)-Tu(t1)|=

从上式可以看出，当t2→t1时上面不等式右边趋于0。因此TU等度连续, 显然也是一致连续的，所以TU是相对紧的,即T是全连续的。由引理1(Schauder不动点定理)可知T在U中至少存在一个不动点，也就是边值问题(1)至少存在一个解。 定理证毕。

3 应用举例

例1 考虑以下分数微分方程

(7)

例2 考虑以下分数微分方程

(8)

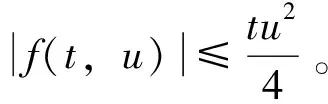
参考文献：

[1] PODLUBNY I.Fractional differential equations [M]. New York: Academic Press, 1999.

[2] SAMKO S G, KILBAS A A, MARICHEV O I. Fractional integrals and derivatives: theory and applications [M]. Yverdon, Switzerland: Gordon and Breach Science Publisher, 1993: 36-37.

[3] KILBAS A A, MARZAN S. Nonlinear differential equations with the Caputo fractional derivative in the space of continuously differentiable functions [J]. Differ Eqn, 2005, 1141: 84-89.

[4] WANG J H, XIANG H J, LIU Z G. Positive solution to non-zero boundary values problem for a coupled system of nonlinear fractional differential equations [J]. International Journal of Differential Equations, 2010: 1-12.

[5] SALEM HUSSEIN A H. On the fractional orderm-point boundary value problem in reflexive Banach spaces and weak topologies [J]. J Comput Appl Math, 2009, 224(2): 565-572.

[6] ZHONG W Y, LIN W. Nonlocal and multiple-point boundary value problem for fractional differential equations [J]. Comput Math Appl, 2010, 59(3):1345-1351.

[7] CHENG Y, ZHU G G. Existence of fractional differential equations [J]. J Math Anal Appl, 2005, 310: 26-29.

[8] ZHANG S Q. Positive solutions for boundary value problems of nonlinear fractional differential equations [J]. Electron J Diff Eqn, 2006, 36: 1-12.

[9] BENCHOHRA M, HAMANI S, NTOUYAS S K. Boundary value problems for differential equations with fractional order and nonlocal conditions [J]. Nonlinear Analysis, 2009, 71(7/8): 2391-2396.

[10] WANG J H, XIANG H J, LIU Z G. Positive solution for three-point boundary value problems of nonlinear fractional differential equation withp-Laplacian [J]. Far East Journal of Applied Mathematics, 2009，37 (1): 33-47.

[11] LIANG S,ZHANG J.Positive solutions for boundary value problems of nonlinear fractional differential equation[J].Nonlinear Analysis; Theory, Methods & Applications, 2009,71(11):5545-5550.

[12] BAI Z, LU H.Positive solutions for boundary value problem of nonliner fractional differential equation[J].Journal of Mathematical Analysis and Applications, 2005,311(2):495-505.