基于残差修正的GM(1,1)模型的我国人均粮食产量预测

杨 阳

（西南政法大学，重庆401120）

0 引言

经济预测指通过对历史数据、现象的总结归纳，发现内在波动规律并构建相关框架和方法，对未来的经济走势进行期望假设的过程。目前预测的方法很多，定性和定量作为预测的两大工具，越来越呈现出互相补充、互为检验的良性关系。定性预测的头脑风暴法、德尔菲法曾经和正在被广泛使用，但定量预测的运用正在被全面推广，如线性计量方程、马尔科夫链、空间状态方程、灰色理论等，各种预测工具各有优劣，甚至相关学者提出使用变权重组合模型对众多预测方法进行整合，以缩小预测误差而提高精度。笔者认为，首先数量经济预测方法（如计量回归）需要大量的数据，那么由于统计资料的缺失或误差导致模型整体效度不高、模型不可能穷尽所有影响因素而引起随机扰动项不真实；马尔科夫链强调无后效性，即当期数据包含了以往历史数据所有信息，下一期现象只与本期数据和转移概率有关，需要强有效市场理论的支持，这些在现实当中是不成立的，所以一切计量预测方法都具备了一些与现实不相符合的假设，必然导致误差。其次变系数组合预测法固然能够取不同预测模型之长以提高精度，但预测模型多种多样，在纷繁复杂的经济现象下不可能将所有的预测方法都使用一次后再进行变系数组合，这样做不仅复杂而且所得出的系数也仅仅是在一小段时间内有效。综上所述，灰色系统能够相对于其他预测模型更能从本质上揭示数据运动规律，并且所需要的样本区间较其他方法少，将由随机扰动项引起的冲击序列进行灰——白转变。但任何模型都存在着预测误差问题，误差反映在模型中为随机扰动项，故本文对GM(1,1)预测模型的尾端残差序列进行白热化方程进行时间相应函数求解，以期消除误差，并通过实际案例进行分析以体现其在经济预测中的价值。

1 残差修正的GM(1,1)模型

目前关于灰色预测方面的理论研究非常多，本文无意于去讨论已经成熟的模型形式，而着重探讨模型中的经济含义和变量作用。GM(1,1)模型表示一阶条件下单变量的灰色预测模型，有基本形式和原始形式之分。

原始形式是指 x0(k)+ax1(k)=b，其中 x0(k)为原始序列，x1(k)为一次累加序列，那么由简单OLS可求出a,b两个参数，具体意义是a为发展系数，及累加序列每变动一个单位给原始序列带来的影响作用大小，成为发展系数。假设x0(k)是一个成倍数增长的简单序列，如x0(k)=Ck，C为常数，那么很容易求出a与b之间存在的简单线性关系。基本形式是计算出x1(k)的紧邻均值序列z1(k)，然后将其替代x1(k)，形成x0(k)+az1(k)=b，替代的目的在于使用累加序列紧邻均值可比较好的控制趋势放大效应，即缓冲算子作用。求得参数a,b的回归矩阵可表示为

则GM(1,1)模型x0(k)+az1(k)=b的最小二乘估计参数列满足x0(k)+az1(k)=b的时间响应函数序列为

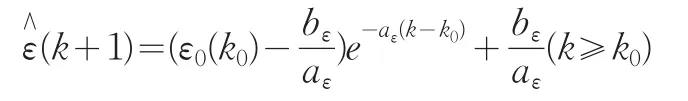
从K0开始的ε0的预测序列为

其中，

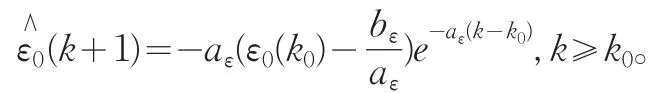
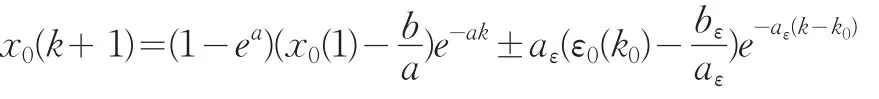
残差修正的GM(1,1)基本理念是：既然原始观测序列存在内部规律可用灰色处理得到提取值那么预测与观测序列所形成的误差必然有一部分属于系统真实序列，同样可以采取时间相应公式处理，克服了以往计量方法无法再从残差即随机扰动项中提取有价值信息的不足。值得说明的是上述提高的K0是截取误差项的起点值，这并不意味着必须要从长度为n的残差序列中后半段开始提取，可以通过比较不同时点上预测误差的大小，进行有针对性的选取，在本文下面的例证中就使K0为2，即全范围的提取，从整体预测角度去减少误差。当然在相关研究中作者们可以根据实际情况选取K0。

2 实证分析

2.1 我国粮食产量的统计分析

根据以上的灰色模型及残差修正分析，选取2000～2009年的我国人均粮食产量为研究对象，数据来源于《中国统计年鉴》（2009）。进行GM(1,1)预测，并通过对尾端残差的1—AGO序列建立时间相应函数求解，对预测模型进行更正。我国作为传统意义上的农业大国，在向工业化强国迈进的道路上一直没有忽视粮食安全的重要性，但自1998年粮食产量达到历史顶峰后，由于耕地面积减少、农村劳动力大量外流和技术基础过低等综合因素2003年粮食不增反减，曾经一度引起恐慌。但中央采取了一系列的“三农”扶持政策，加大了对农业的政策倾斜力度与投资，克服了干旱等自然灾害，实现了七连增的大丰收。但也应清楚的认识到虽然粮食总量连年增加，但增加的幅度很小，以2000年为基数2009年的增加幅度为14.85%，年平均增长率不到1.5%，不仅小于国家在农业投资上的增速也小于农民收入增速，体现了粮食增产工作是系统工程，需要各项支持协同努力才能够发挥显著效果，目前的粮食政策有待改善。人口众多是我国的一大基本国情，人口的增长在短期内并不意味着劳动力的增多，所以经济不会以新古典经济增长模型中的劳动力添加模式发展，实际上降低了人均占有资源，有学者经过统计改革开放24年以来人均粮食产量划了一个圈-回到了原点。上述观点可从表1看出。人均粮食产量由总产量和国民人数决定，过低一方面体现了粮食产量增速缓慢，另一方面也反映了计划生育在我国的执行力度不够，没有达到相应的目标。

2.2 粮食产量GM(1,1)预测

灰色预测是使历史数据序列由灰转白的过程。根据第一节的理论叙述，经过以下流程对人均粮食产量进行预测：

表1 我国粮食总产量及人均产量

（1）累加生成序列1-AGO的生成

根据系统观测行为序列

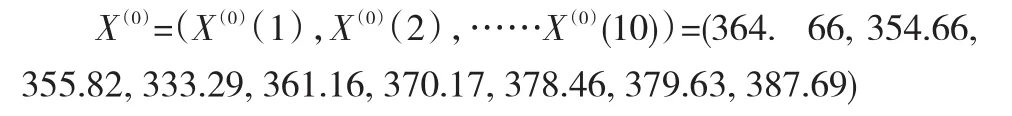
得到1-AGO序列：

运用数据序列进行灰色系统建模的前提是序列X（0）为非负准光滑序列，而X（1）具有准指数规律，下面进行验证。首先进行X（0）光滑比P（k）值计算，结果如表2。表2中2001年的P（k）值为0.972，其他年费均小于0.5，而P（k+1）/P（k）在八个时点上均通过检验，故认为考察时间段内非负准光滑序列验证通过；同理，得到前后年数据之比O（k），数据同见表1，浮动区间为[0.9367,1.0836]，极值＜0.5,可知数据序列存在准灰数指数规律。

（2）紧邻均值Z(1)生成及预测模型估计

上文已经通过了灰色建模的前提条件检验，生成紧邻均值序列

由于白热化方程的形式为X(t)+aZ(t)=b，通过最小二乘法进行估计的矩阵形式是

表2 非负准光滑序列及准指数规律验证

得到发展系数为0.0149，绝对值小于2说明GM模型稳定，并且根据[-2/(n+1),2/(n+1)]原则，有较高精度。则可得到相应的时间函数式22880.504304，经过DPS软件测算后得到拟合序列，见表3。

表3的第三列为预测误差，第四列为相对误差，发现拟合效果不好，残差平方和C为0.7046，平均相对误差P=0.5556。对未来5期进行预测得到 X(t+k)=399.16069，405.15455，411.23841，417.41363，423.68157。

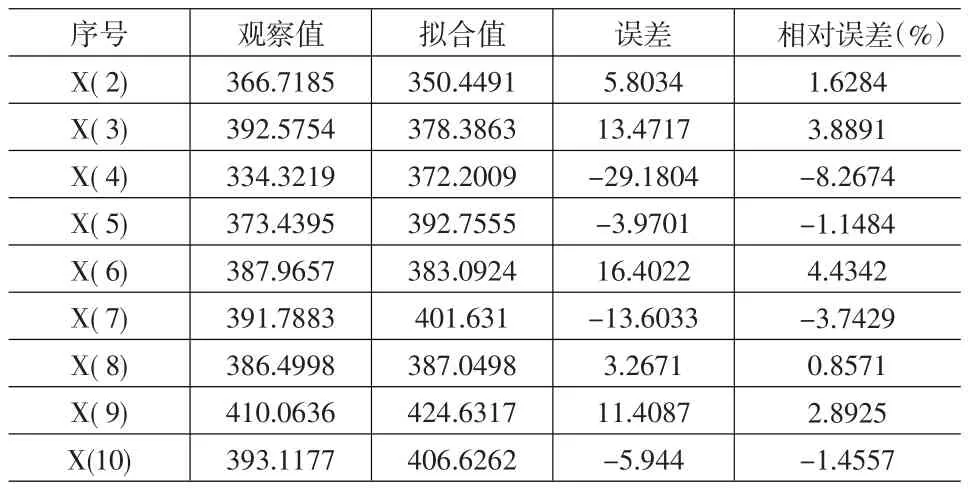
表3 DPS处理的GM(1,1)预测结果

3 残差序列修正的模型

根据上述讨论目前所得到的结果并不良好，根据误差序列均取绝对值，得到

建立GM（1，1）模型，得 ε0的1-AGO序列 ε1的时间响应式

其中，a=0.101709，b=18.984327。其导数还原值为

得到残差修正后的预测模型为

预测的模型拟合值、残差序列、相对平均误差见表4。残差平方和提升到0.8889，模型评价结果为好。对未来5年的预测结果为：394.35298，399.69133，405.18307，410.82343，416.60824公斤/人。从这里反映了两个问题：一是由于粮食产量为明显上扬序列，进行模拟预测时残差的扩大是由于趋势的放大效应一起的，残差修正后的预测模型比未修正条件下的更具有收敛性，从预测结果对比可看出，修正结果较以前波动小。

表4 残差修正后的GM(1,1)预测结果

灰色理论认为当两个波动序列形状和趋势越接近，则两者之间存在灰色关联关系，这里通过实际序列和两个预测序列之间的关系图（图1）可以看出，修正后的预测序列更与实际序列接近，而与传统预测方法存在的根本差异在于：灰色理论认为行为序列（即实际值）并不是真实序列，而灰色处理的任务就是从行为序列中提取真实序列并消除扰动项，但其他方法却与此相反，大多方法以观测序列为实际序列。

3 结论

经过基于残差修正的GM(1,1)预测模型相关讨论和实证，得到以下结论。

(1)灰色模型无论是在理论基础还是实践运用中均较其他计量模型更为实用和简便，且不失逻辑基础。现实经济社会活动纷繁复杂，建立模型时不能包含全部因素，并且由于统计手段的局限性数据缺漏是常见现象。王明礼认为灰色模型是指利用离散随机数经过生成变为随机性被显著削弱而且较有规律的生成数，建立起的微分方程形式的模型，是一个将信息由灰变白的过程。缓冲算子的提出使得原始数据的处理更具规律性、可控性和系统性，能够根据实际经济现象和发展趋势对原始数据进行调整，摈弃了以往观测数据等于真实数据的误区。

(2)灰色系统残差修正克服了其他计量模型不能对随机扰动项进行再次提取有效信息的缺陷，更重要的是从残差序列本身入手，不会带来如回归方法中增减自变量带来的伪回归和异方差，并且这种残差修正过程可以多次进行，直到残差信息被很好提取为止。本文实证中的结论证明了残差修正使预测精度大大提高，通过了相关检验。并且缓冲算子的存在也使灰色算法与其他算法结合得以实现，如姚作芳等使用markov法对灰色预测结果进行修正；张大斌(2009)提出了一种基于遗传算法调整发展系数和内生灰作用量的灰色预测模型,将遗传算法系数作为灰色缓冲算子。

（3）我国粮食产量预测情况说明，未来5年我国人均粮食产量增速要小于以前，年增量为5～6公斤/人，小于2003～2009期间的8～10公斤/人。当然，预测的结果是基于目前发展态势的前提，如果产业政策和科技水平有了很好的调整，情况会发生相应变化，特别是党的十七大上提出的确保粮食安全、建设产量基地等大力发展粮食产业的措施，这些都会造成系统行为规律的变动。粮食产业包含很多子行业，如水稻、玉米和小麦行业，需要寻找对粮食产业贡献最大的子产业，进行区别财政支持。目前有学者对粮食产业结构进行分析，赖红兵通过建立粮食产量的误差修正模型,发现水稻波动对粮食产量波动的影响显著,其次是玉米和小麦。对提高粮食产量这项国家任务需要进行定量分析，以确保粮食产业稳步发展。

图1 预测效果对比图

[1]邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1987.

[2]王明礼.三种灰色系统模型的预测比较[J].统计与决策，2011,（8）

[3]姚作芳,刘兴土,杨飞.马尔科夫方法修正的灰色模型在吉林省粮食产量预测中的应用[J].地理科学，2010,（3）.

[4]张大斌,朱侯,李威,张景广.一种基于遗传算法的灰色模型在铁路客运量预测中的应用[J].统计与决策，2009,（24）.

[5]赖红兵.中国粮食产量波动及其结构分析[J].农业技术经济，2009,（5）.