自适应变系数面板数据模型的半参数估计

武大勇，周永卫

（郑州航空工业管理学院 数理系，郑州 450015）

0 引言

假设我们要估计G(x)=E[Y|X=x]，这里Y为被解释变量，X为 p×1维解释变量，在本文中，我们对于回归函数G(x)利用下面形式的变系数模型做近似：

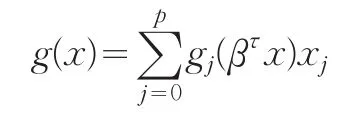
这里 β∈ℜp为一方向参数系数 g(˙)=(g0(⋅),g1(⋅),…,gp(⋅))τ为未知函数，我们将选择方向参数β和系数函数gj(⋅)使得E[G(x)-g(x)]2达到最小。我们所给出的这种自适应变系数模型与一般的变系数模型相比具有如下有点：一旦β给定，对于未知函数g(⋅)的估计我们很容易利用一维局部线性核估计的方法得到，而且，系数函数g(⋅)的图像也很容易画出，这或许对分析函数g(⋅)是如何变化的非常有用。另外，当模型中的βτx固定时，模型（1）包含更多关于解释变量xj的形式，如xj的平方项、xj的交叉项等，因此此模型对于捕捉作为解释变量的xj的非线性结构更具有实用性和灵活性。

在本文中，我们将把上面的自适应变系数模型中推广到面板数据中，以得到自适应变系数面板数据模型。对于变系数面板数据数据模型中的非参数或半参数估计，已有一些结果，如Cai and Li(2005),Cai and Xiong(2006),Cai and Li(2007)中考虑了变系数动态面板数据的非参数估计，Fan,Yao和Cai(2003)还考虑了一种自适应的时间序列模型的非参数估计，但是对自适应变系数的面板数据模型利用半参数的方法还没有相关的文献。

本文将介绍一种有效的后适应算法来估计未知函数g(⋅)，来选择的核估计通过Monte Carlo试验，对于上面所给出的估计从两个具体的例子做出验证。

1 自适应变系数面板数据模型

在本文中我们考虑一种半参数的面板数据模型（自适应变系数面板数据模型），我们假设模型有如下形式：

这里 Xi,t为 p×1维的，且第一个元素为1，系数函数g(˙)是ℜp空间里的光滑函数；β为 p×1维的未知参数，且误差项假设为独立同分布(i.i.d)的。在本文中我们主要的结果都是建立在Xi,t是纯外生变量的基础上，即 E(εi,t|Xi,t)=0 。

则模型（1）可被改写为：

在模型（1）中包含许多我们所熟悉的模型，如若β=1，即

上模型一般称为变系数面板数据模型，对模型（3），Cai和Li(2005),Cai和Xiong(2006),Cai和Li(2007)得到了函数系数g(Xi,t)的非参数广义矩估计和估计的渐进正态性。并且，从后面我们的分析知自适应变系数面板数据模型（1）比一般的变系数面板数据模型（3）所要估计的参数要少得多，避免了估计参数过多而引起的参数灾难问题，因此应用起来也更方便、有效。

此模型就是一般的面板数据回归模型，对于模型（4），Arellano(2003),Baltagi(2005),Hsiao(2003)得到了参数的广义矩估计，后来，Byeong,Robin和Leopold(2007)利用一类特殊的矩条件，得到了此模型参数的半参数估计，并对参数估计的性质从理论和数值试验上得到了验证。

因此，模型（1）所包含的形式显然要比模型（3）和（4）要多，这样我们就可以通过选择与模型独立的参数β的方位来减少估计的偏，同时，对于参数β在我们进行并不会为我们的参数估计带来额外的困难。实际上，参数β通常只估计出它的数值解，而非参数函数g(˙)在参数β已知的条件下很容易被估计出。

2 半参数估计

对于模型（1），这里将介绍一种剖面最小二乘估计(Profile Least-Squares Estimation)的方法，对于模型中出现的参数β和变系数函数g(˙)给出估计。这种方法的基本思想是对于给定的参数 β ，首先找到非参数项 g(˙)的估计，然后用估计出的参数函数再来估计未知的参数项β，即在模型（2）中，用替换掉 g(˙)后可得合成参数模型

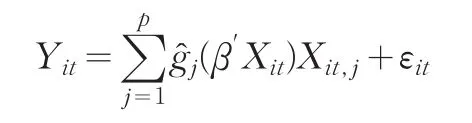
（1）若给出 β ，非参数项 g(˙)的估计

对于给定的系数β=β0已知，我们假设为二阶连续可微的函数，则对于给定的和其邻域内的利用Taylor公式展开有z)，这里则估计未知函数g(˙)可转化最小化下面的式子

这里w( ⋅)为定义在一个有界支撑上的有界权函数，它用来控制边界效应。函数为定义在紧支撑上的一对称的概率密度函数。h为窗宽，用它来控制估计的精确性。

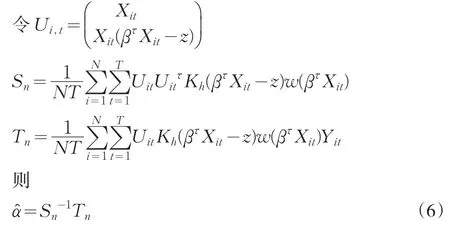
(2)若给出 g(˙)的估计 g(˙)，估计参数 β

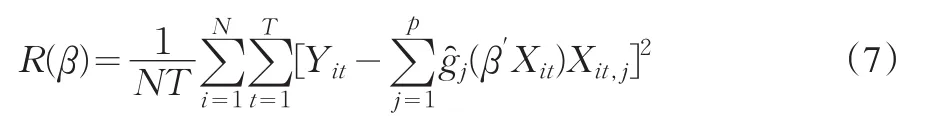
若令实际上R(β)就是未知函数g(˙)的估计的残差，它的大小从一个方面说明了我们所给出估计的好坏。若已知g(˙)的估计g(˙)，估计参数β的过程实际上相当于关于β最小化R(β)的过程。但是，由于非参数项 g(˙)的估计 g(˙;β)依赖参数β，因此关于β直接最小化（7）式是非常困难的，下面利用Newton-Raphson迭代的方法得到参数β的数值解。

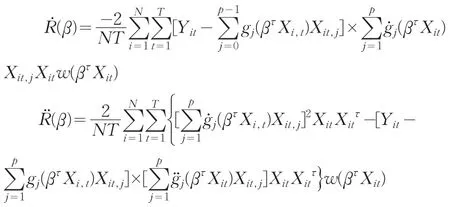
由（7）式可得

3 最优窗宽的选择

上述参数和非参数估计的好坏依赖于核估计中窗宽的选择，因此如何选取最优的窗宽使我们的估计更有效是必须讨论解决的问题。根据Craven and Wahba(1979)提供的选择最优窗宽的广义交叉核实方法（the generalized cross-validation method），对 于 给 给 定 的 β ，令显然

这 里 H(h)是 一 个 n×n矩 阵 ，显 然 其 与是独立的，根据广义交叉核实方法(GCV)，选择h最小化

最小化上式可得最优窗宽为

这里n=NT，其中的系数c0,c1,c2可根据Ruppert(1997)提供的方法获得。为了计算tr(H(h))，对于给定的1≤l≤N;1≤s≤T ，有：

这里Ο为 p×1维元素全为0的列向量，令

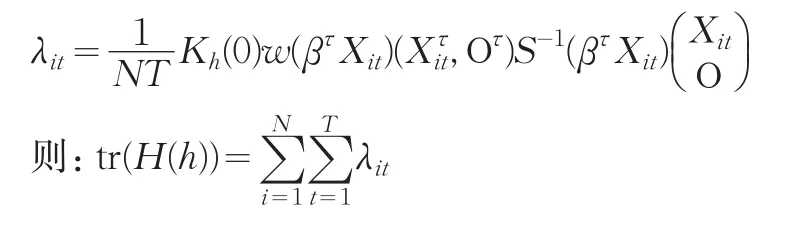
4 算法

（2）对于可供选择的窗宽的值hk,k=1,…,q，重复下面的步骤（a）和（b），直到两次迭代中（7）式 R(β)的差别足够小：

（a）对于给定的 β ，按照（6）式来估计 gj( ⋅)；

（b）对于给定的gj( ⋅)，按照上面所给的方法来估计β；

（3）对于k=1,…,q，用β的估计值来计算GCV(hk)，令c1和c2为最小化下式所得

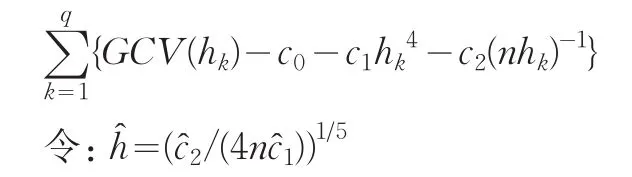
5 Monte-Carlo试验

考虑如下面的面板数据模型

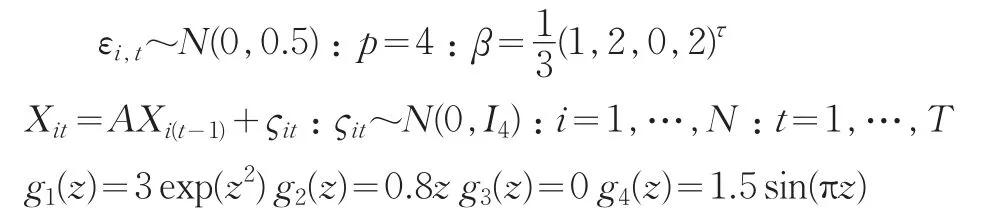
模拟结果如表1。

表1为模型（10）的模拟，在这里核函数取的为Gauss核函数，即

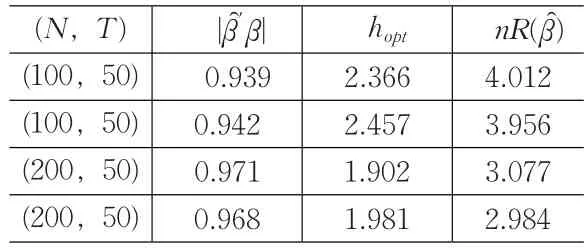
表1

由上例的模拟结果可以看出，对于一个未知函数g(⋅)，估计的残差是比较小的；同时，残差对于样本容量的选取有一定的依赖，当样本容量有显著增大的时候，残差也随之变小。

[1]Arellano,M.Panel Data Econometrics[M].Oxford:Oxford University Press,2003.

[2]Baltagi,B.Econometric Analysis of Panel Data（2ndEdition）[M].New York:John Wiley and Sons,2005.

[3]Byeong,U.P,Robin,C.S.,Leopold,S.Semiparametric Efficient Estimation of Dynamic Panel Data Models[J].Journal of Econometrics,2007,136.

[4]Cai,Z,H.Xiong.Efficient Estimation of Partially Varying Coefficient Instrumental Models[C].Department of Mathematics and Statistics,University of North Carolina at Charlotte,2006.

[5]Cai,Z.,Q.Li.Nonparametric Estimation of Varying Coefficient Dynamic Panel Data Models[C].Department of Economics,Taxes A&M University,2005.

[6]Cai,Z.,Q.Li.Nonparametric Estimation of Varying Coefficient Dynamic Panel Data Models[R].The Wang Yanan Institute for Studies in Economics,Xiamen University in China,2007.

[7]Horowitz,J.L.,M.Markatou.Semi para metric Estimation of Regression Models for Panel Data[J].The Review of Economic Studies,1996,63.

[8]Hsiao,C.Analysis of Panel Data(2ndEdition)[M].Cambridge:University Press,2003.

[9]Kniesner,T.J.,Q.Li.Nonlinearity in Dynamic Adjustment:Semipara metric Estimation of Panel Labor Supply[J].Empirical Econometrics,2002,27.

[10]Fan,J.,Yao,Q.,Cai,Z.Adaptive Varying-coefficient Linear Models[J].Journal of the Royal Statistical Socient,Series B,2003,(65).

[11]Ruppert,D.Empirical-bias Bandwidths for Local Polynomial Nonparametric Regression and Density Estimation[J].Journal of the American Statistical Assiociation,1997,(92).