轴向磁化永磁轴承的刚度特性分析

张钢，殷庆振，阮娟，蒋德得，高刚

(上海大学 机电工程与自动化学院，上海 200072)

永磁悬浮是利用永磁体之间的作用力来实现悬浮物体在全部或部分自由度上的稳定悬浮，它不需主动电子控制系统，不仅节省了电力消耗，更重要是省掉了可能失效的复杂的控制系统部件，使系统更加可靠，使用寿命更长，具有结构简单、工作可靠、无磨损、能耗小等突出优点。永磁轴承可与电磁轴承、机械轴承、空气轴承和超导体磁轴承等相结合，构成各种形式的磁轴承系统，具有广泛应用前景[1-2]。

在永磁轴承设计中，磁轴承本身承载能力和刚度十分重要。其承载能力可以通过堆叠以及恰当的结构设计实现高承载力、高刚度来满足要求。阻尼可以通过引入机械阻尼器、电磁阻尼器来实现转子系统的动力稳定。

针对永磁轴承力学特性，国内、外学者进行了大量的工作，建立了各自的模型及计算公式[3-6]，但针对永磁轴承支承转子系统的具体研究还十分不足。下文以轴向磁化的永磁轴承为研究对象，建立永磁轴承的刚度矩阵，分析永磁轴承尺寸参数对各刚度的影响。

1 永磁轴承的分析模型

为便于建立解析模型，取一个动磁环和相邻的一个静磁环作为研究对象，建立如图1所示直角坐标系，一对磁环在坐标系中的坐标为：上磁环中心坐标(0,0,z2)，下磁环中心坐标(0,0,z1)。环外径为R, 磁环高度为b, 磁环厚度为a。

图1 单个轴向磁化永磁轴承空间坐标系

2 永磁轴承的刚度矩阵

在悬浮系统中，由于转子绕z轴转动，不考虑绕z轴旋转自由度，因此刚度矩阵是5×5矩阵[7]。

(1)

坐标变换到柱坐标系中，磁体为圆柱体，则Kxx=Kyy=Kr，Kαα=Kββ=Kφ；磁场是保守场，因此刚度矩阵为对称阵，即Kij=Kji。

在转子处于中心位置时，沿z轴移动磁环，径向力始终为零，因此除Kzz=Kz之外，第3行和第3列都为零。

沿x轴移动磁环，力Fy和力矩Mx始终为0，因此，Kyx=Kαx=0；同理Kβα=Kxα=0，Kyβ=Kβy=0。因此在柱坐标系中，5自由度永磁轴承-转子系统的刚度矩阵可简化成

(2)

式中：下标r,φ,z分别代表相应矢量在径向、周向和轴向的分量。

由Earnshaw定律可知[8]：2Kr+Kz=0，因此只需考虑3个未知刚度的值。

2.1 力与力矩的推导

运用等效电流法分析永磁体的受力，由洛仑兹定律可得力的计算公式[9]

(3)

磁学基本公式可得[10]

(4)

(5)

(6)

由上式推导得到圆柱永磁体的轴向力和y轴力矩。

Fz=2πRJφ[Aφ(R,z2+0.5b)-Aφ(R,z2-0.5b)]，

(7)

My=-JφBz(Rcos2φzsinφy-z2cosφzcosφy)+

JφBr(Rsin2φzcosφz+Rz2cos3φzcosφy+

z2cos2φzsinφy)。

(8)

2.2 刚度矩阵表达式

径向刚度[10]

(9)

倾斜刚度

2aΛ(Ri,z)+a(2R-a)μ0Φ(Ri,z)+

2az(2R-a)Bz(Ri,z)+(3aR2-az2-

(10)

式中：Φ，Λ分别为永磁体的标量势和矢量势积分；R1=R；R2=R-a。

耦合刚度

(11)

3 无量纲化和参数影响规律

3.1 尺寸参数对轴向力的影响

使用Matlab编制计算程序，得到无量纲轴向力随无量纲轴向距离的变化曲线如图2所示。

图2 无量纲轴向力随无量纲轴向距离的变化曲线

(12)

表 1 比例系数Pz值

图3 比例系数变化曲线

图4 比例系数变化曲线

分析表1可以得到：当R/a>3时，变化范围小于2%，即可以忽略外径对无量纲轴向力的影响。

图随和的变化曲线图

3.2 尺寸参数对径向刚度的影响

选择标准径向刚度为

(13)

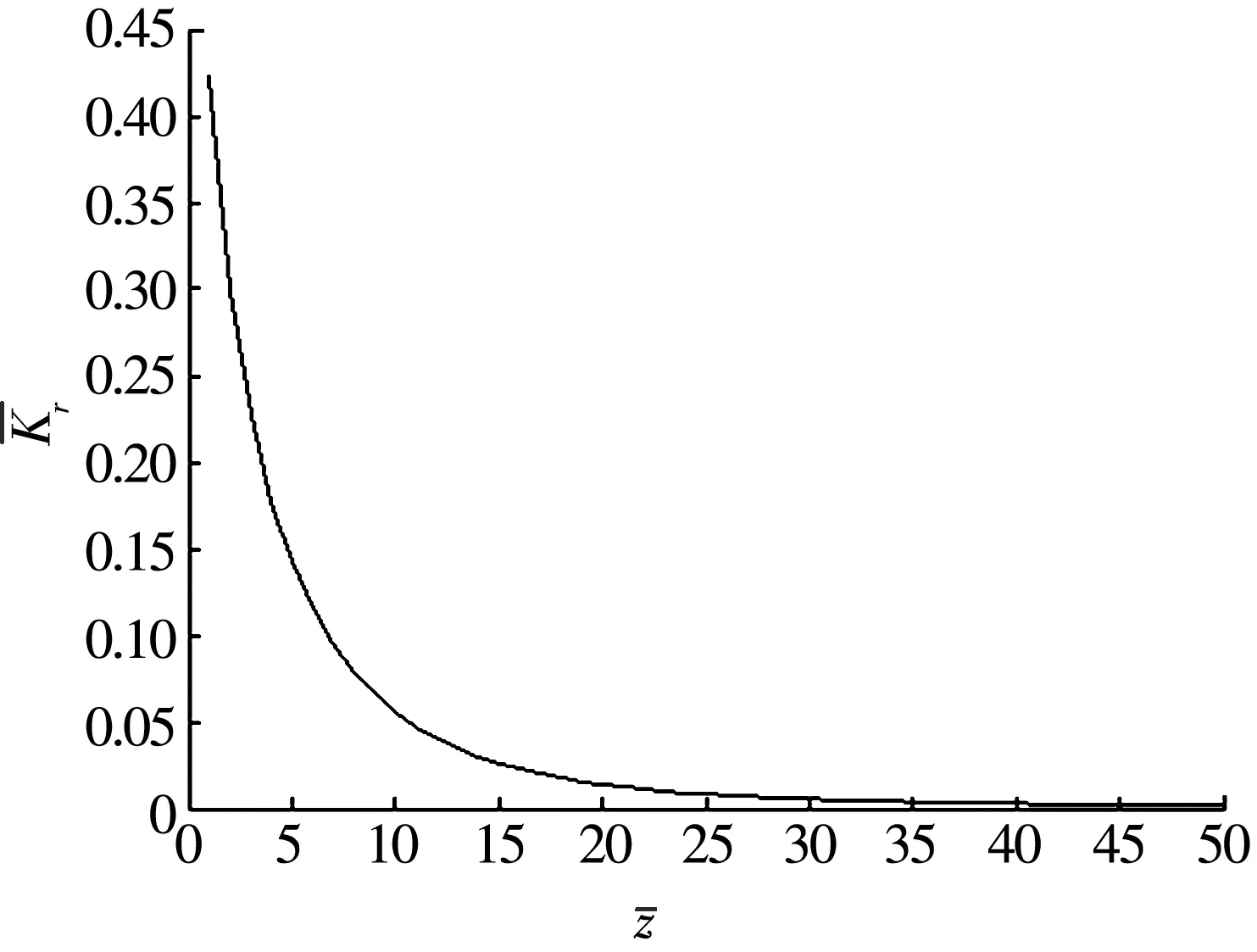
图随的变化曲线

定义径向刚度比例系数

(14)

图7 比例系数变化曲线

图8 比例系数变化曲线

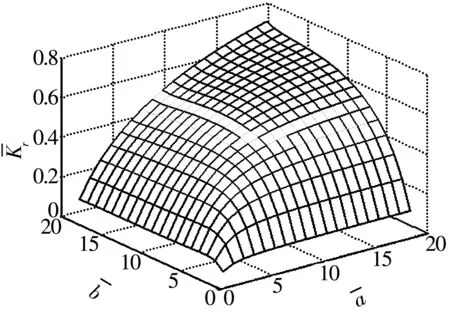
图随和的变化曲线图

3.3 特定轴向力和径向刚度的优化

以单位体积产生的轴向力和径向刚度最大为目标，对一对磁环构成的永磁轴承进行优化。一对永磁轴承所占体积为

V=πb(2a+h)(R0+Ri),

(15)

则单位体积轴向力和径向刚度为

(16)

图10 单位体积轴向力随和的变化图

在设计中，由于单对磁环刚度有限，为满足实际要求，可通过采用堆叠的形式来提高刚度。

图11 单位体积径向刚度随和的变化图

3.4 尺寸参数对倾斜刚度的影响

定义标准倾斜刚度为

(17)

外径对倾斜刚度的影响如图12所示。通过图12可以看出，外径对倾斜刚度的影响不能像轴向力和径向刚度那样忽略。

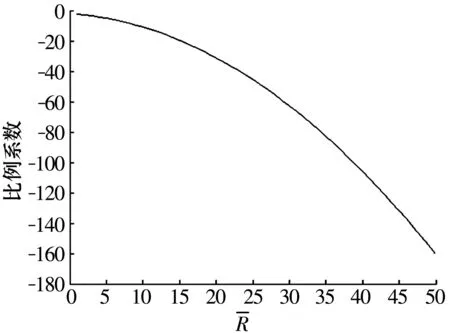
图12 比例系数变化曲线

图随和的变化曲线图

3.5 尺寸参数对耦合刚度的影响

定义标准耦合刚度为

(18)

耦合刚度比例系数Pφr为

(19)

耦合刚度随磁环外径的变化规律如图14所示。

图14 比例系数变化曲线

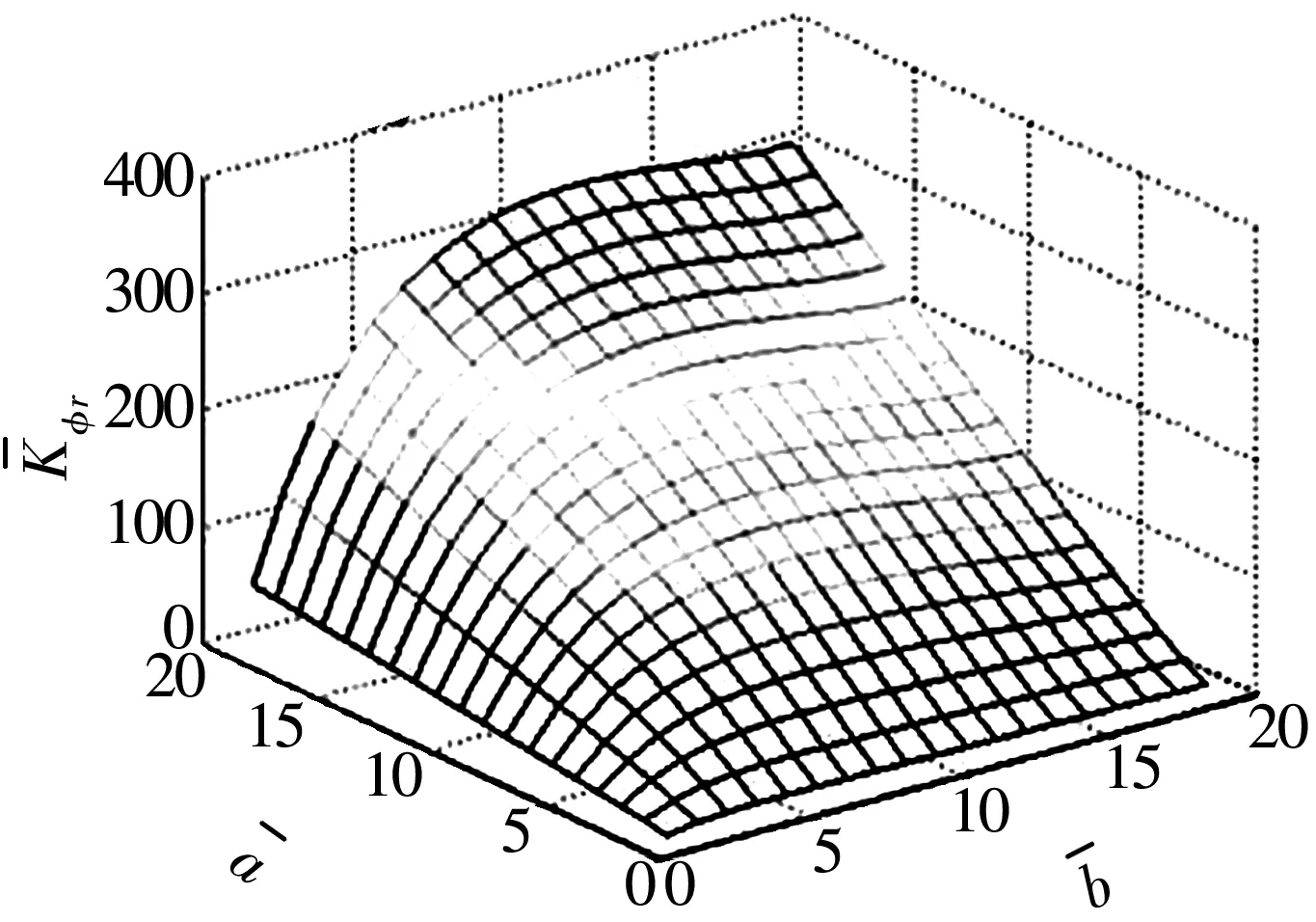
图随和变化图

4 结论

(1)在轴向力和径向刚度分析中，当R/a>3时，磁环外径作为弱影响参数而可以被省略。

(2)在倾斜刚度和耦合刚度分析中，外径的影响不能被忽略。

(3)当磁环高度和厚度相等时，永磁轴承性能最优。

在永磁悬浮系统中，永磁轴承刚度矩阵中的各个刚度是研究永磁轴承-转子系统动力学的基础，它们对永磁轴承-转子系统的稳定性起着十分重要的作用。