紫檀冲水库劈裂灌浆时主坝塌陷分析
龙起华 石自堂 王 磊
(武汉大学水资源与水电工程科学国家重点实验室 湖北 武汉 430072)
1 工程概况
紫檀冲水库主坝为粘土心墙坝,坝顶高程173.6m,最大坝高46.2 m,坝顶宽5.33m、坝顶长200m。上游坝坡采用块石护坡,无垫层料,坡比自上至下为1∶2.11、1∶2.36。下游坝坡采用草皮护坡,坡比自上至下 1∶1.71、1∶2.03、1∶2.23、1∶1.74。坝顶防浪墙高0.4m。心墙坡比1∶0.15,心墙顶宽度1.4m。由于粘土来源不足,原设计心墙核心部分,用粘土回填,其他部分用重壤土回填;由于粘土质量差,人工碾压不密实,防渗效果不好,坝基多处渗水,由ZK02、ZK03钻孔揭示主坝心墙墙顶距坝顶地表4.9m,心墙墙顶高程为168.61m,比设计洪水位170.92m低2.31m,比校核洪水位171.90m低3.29m,比正常蓄水位169.30m低0.69m,并且心墙未与防浪墙墙底部连接,不满足大坝防渗要求。
2 主坝塌陷事故描述
针对《紫檀冲水库工程地质勘察报告》所揭示主坝存在的缺陷,采用劈裂灌浆对主坝进行加固,沿坝轴线方向设置灌浆孔,对坝体进行劈裂灌浆[1]。
在对主坝进行劈裂灌浆施工过程中,2010年7月4日发现桩号为0+094~0+102段坝顶坝面发生塌陷,但并未起足够关注。2010年9月1日进行复灌,在复灌过程中9月16日下午发现主坝桩号0+080~0+152段出现双排裂纹,同时桩号0+088~0+118坝面出现塌陷,坍塌部分宽0.5~0.6m,深度0.4m至0.5m不等,局部桩号处塌陷深度达到0.6m,由于塌陷范围较大,立即停止灌浆施工并同时对大坝整体完整性、大坝沉降、位移进行观测。经观测,坝顶塌陷处均位于心墙上方,大坝除坝顶坝面出现较明显裂缝、坝面坍塌外,其余坝坡等部位均未出现裂缝、坍塌现象,主坝坝体轴线及横向均未出现较明显位移,竖直方向上,除塌陷处有较明显的竖直位移。大坝坝顶其他部位均未出现明显竖直方向位移,同时,个别灌浆孔出现析浆现象,下游坝坡局部地区也出现析浆、冒浆现象。
3 塌陷成因分析及处理措施
3.1 塌陷成因分析
大坝坝顶出现较大部位塌陷后,立即对塌陷部位进行调查,调查后认为除险加固前,主坝缺陷已经存在,甚至可能在主坝下方已经长时间存在一条沿着坝轴线的空洞。
根据塌陷部位宽度的测量,塌陷部位宽度为0.5m~0.6m,假设主坝裂缝及塌陷是由于在加固过程中劈裂灌浆设计不合理造成的。根据此假设,劈裂灌浆施工中,灌浆压力过大,大坝被泥浆劈裂成上下两部分,大坝轴线处形成较宽的裂隙,从而造成塌陷,则由此大坝坝体沿横向x方向势必形成较大的相对位移,知道此相对位移不会比塌陷部位宽度小很多。但实际测量结果却与之有较大差别,根据后期测量结果,大坝坝顶上下游各个观测点间相对位移较小,大都分布在5mm~7mm的范围内,局个别相应点间相对位移达到9mm。这说明,裂缝是由于劈裂灌浆设计不合理造成的是不可靠的。且根据灌浆帷幕原理,灌浆压力设计中包括起始劈裂压力、单孔最大压力、屈服压力设计。在坝体灌浆施工记录中,明确记录灌浆起始劈裂压力为0.6MPa,正常灌浆工作压力为0.3MPa,符合灌浆设计要求,不存在灌浆压力过大导致大坝塌陷问题[2]。
在灌浆开始前,大坝坝体已经存在缺陷,主坝下方可能长时间存在一条沿坝轴线方向的空洞,当开始向灌浆孔灌浆时,由于坝体应力的突然变化,加之泥浆对坝体的湿陷作用,空洞下方土体沉降,而空洞上方土体应力急剧减少,最终坍塌。针对这种意见,必须弄清楚两个问题:①大坝坝顶下方沿轴线方向空洞的形成原因。②大坝坝顶会在劈裂灌浆的时候发生集中坍塌现象的原因。
坝顶发生坍塌后,重新对坍塌部位进行实地勘察,坍塌部位均处于坝轴线上,坍塌部位下方正好是大坝心墙所处位置,坍塌部位并不连续,局部未坍塌部位下方存在连贯空洞,这一点印证了造成坍塌的第二种意见是比较符合事实的。基于空洞的形状及所处的位置,比较合理的观点的是大坝心墙逐年沉降的结果。
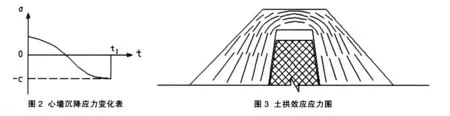
关于心墙沉降量的计算,可以根据土石坝沉降的非线性变弹性理论计算[3]。该理论通过土体三轴压缩试验并在试验基础上,建立邓肯—张模型(Duncan J.M,Chang C.Y.)的土体结构关系模型,该模型把应力应变关系近似地用双曲线表示,如图1所示。根据摩尔—库伦破坏准则和压缩试验公式得到土的切线变形模量的表达式:
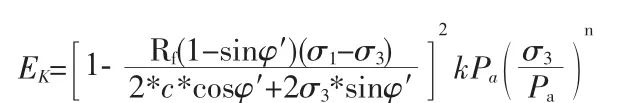
式中:σ1、σ3为填土第一、第三主应力;c、φ′为填土有效凝聚力和内摩擦角;k、n为试验常数,在试验的应力应变曲线上求得;Pa为大气压力,可取近似值为100kPa。
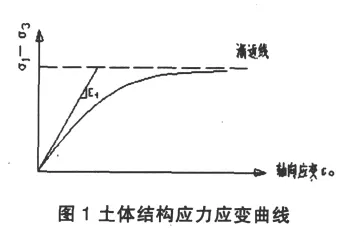
计算心墙沉降采用无侧限条件下的沉降计算公式计算,压缩量的计算公式为:
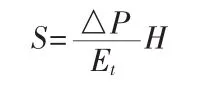
式中,S为土体的竖向压缩量;△P为压力增量;Et为压缩模量,反映单向压缩时土体对变形的抵抗能力;H为土层的高度。
再根据变形模量与压缩模量的关系[3],最终得到坝体在自重应力下沉降的计算公式:
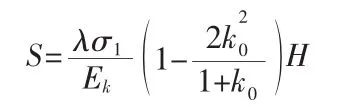
式中,λ为考虑土体侧向应变和拱效应的应力修正系数,k0为静止土压力系数。
在计算心墙沉降时,采用分层计算的方法,根据现场取土试验,心墙密度取1920kg/m3,Rf取 0.9,λ 取 0.6,k=275,n=0.37,=15°,c=21kPa。计算结果如表1所示。
根据计算结果,自该土坝建成以来,心墙沉降量达到0.387m,考虑到坝体填筑时,坝壳填筑材料为粗粒砂土,填筑代料大于0.075mm的砂、砾石含量达61.2%,可以认为坝壳填筑时,即已完成排水固结,因此建成后坝壳沉降量很小或者没有,而心墙主要由粘土和壤土组成,排水固结较慢,土坝建成后,心墙沉降一直持续,自建成至今,沉降量已达0.387m,这就很好地回答了大坝坝顶下方存在沿轴线方向空洞的问题。
既然大坝坝顶下方空洞已经长时间存在,为什么在大坝运行的足够长时间里面并没有发生坍塌,而偏偏在对大坝进行劈裂灌浆时造成了坍塌呢?要解决这个问题,有必要对坝体建成后在自重作用下坝体的应力、应变、沉降进行模拟,分析坝体受力变形情况。大坝刚建成时,大坝坝体与心墙是完全接触、相互挤压的,心墙与坝体接触面上存在的应力是压应力,方向垂直接触面,如图2所示,在随后的时间中,随着大坝心墙的沉降,心墙顶部与大坝坝顶间的压应力越来越小直至为0,随后变为拉应力,该拉应力由坝体填土的凝聚力提供,随着时间推移,沉降增加,最终凝聚力不足以支撑心墙与坝顶上方填土间的拉应力从而导致心墙与坝顶的分离。在心墙与坝顶分离的这一过程中还同时进行了坝顶土体应力的重新分配,坝顶心墙上方的填土在大坝刚建成时是靠下方的心墙提供向上的力支撑的,而随着心墙的沉降,心墙不再为上方的填土提供支撑力,该支撑力正好由心墙顶部两边的填土提供,并最终形成一个拱,这就是“土拱效应”[4][5],如图3所示。当没有外力干扰或土拱上方的力不足与破坏土拱时,该土拱是稳定的,这就是大坝坝顶下方存在空洞而在长时间内并没有坍塌的原因。但是,当对主坝进行劈裂灌浆时,起始劈裂压力大于土拱顶部土体的压应力,使填土间应力由压应力变为拉应力并最终在拉应力大于填土间凝聚力的时导致坝顶终塌陷。
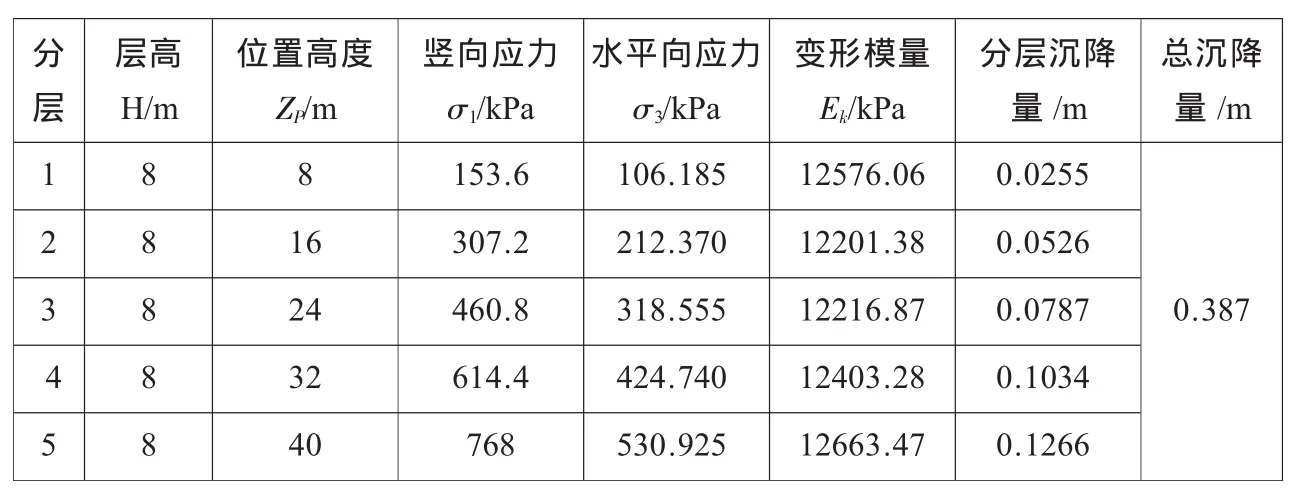
表1 心墙总沉降量计算表
3.2 处理措施
针对该土石坝的渗漏情况,由于上面已经排除了劈裂灌浆对土石坝坝体危害的影响,因此仍然可以对土石坝进行劈裂灌浆,但应该提高劈裂灌浆的质量,更好的控制灌浆压力,并推荐增加复灌次数,复灌时间间隔也要严格把握,推荐复灌时间间隔不小于5天。
针对土石坝坝顶的塌陷情况,推荐坝顶开挖重新填筑,开挖深度最好超过心墙顶部高程,而后用粘土及坝壳代料重新回填压实,最终回填到设计坝顶高程。
4 结语
(1)大坝坝顶坍塌主要是由于心墙沉降及劈裂灌浆时劈裂压力、泥浆湿陷作用造成的。劈裂灌浆并没有造成坝体整体结构受到破坏,相反,劈裂灌浆可以促使坝体应力重新分配,补充坝体小应力不足,对大坝的稳定是有利的。
(2)由于进行了劈裂灌浆,坝体心墙在泥浆的湿陷、挤压作用下,裂缝及孔隙已经被泥浆充填,且心墙更加密实。劈裂灌浆已经充分补充坝体心墙的应力不足,提高了坝体心墙的稳定性,且心墙已经经过了三十多年的沉降,沉降已经基本完成,因此不必担心在对土坝进行除险加固后,会继续产生裂隙甚至空洞。
(3)始建于同一时期、在同等生产力条件下的建成的心墙土坝,大都存在心墙与坝壳的不均匀沉降问题,该论文探讨了在对该类土坝进行劈裂灌浆时出现的问题及解决措施,为这一类土坝进行除险加固提供了理论基础。陕西水利
[1]孙晓杰,任传英,马兆会,郑绪刚.浅谈劈裂灌浆在土坝堤防防渗处理中的设计与应用 [J].China science and Technology Review,2009,36:319-320
[2]白永年.中国堤坝防渗加固新技术[M].北京:中国水利水电出版社,2001.9
[3]王春宁,刘智杰,周琼.土坝沉降的非线性变弹性计算[J].湖南水利水电,2002,5:7-15
[4]宫必宁,童蕾,牛志国.土石坝工程的拱效应分析 [J].东北水利水电,2004,(12):14-15
[5]张家松,李欣,牛志国,林清安.土石坝粘土心墙拱效应分析 [J].水利科技与经济,2007,(2):84-86

