铝合金轴心受压构件的稳定性研究与数值模拟

翟希梅，吴 海，王誉瑾，范 峰

（哈尔滨工业大学 土木工程学院，150090 哈尔滨，xmzhai@hit.edu.cn）

铝合金轴心受压构件的稳定性研究与数值模拟

翟希梅，吴 海，王誉瑾，范 峰

（哈尔滨工业大学 土木工程学院，150090 哈尔滨，xmzhai@hit.edu.cn）

为了给试验提供可靠的依据与指导，采用有限元软件ABAQUS对17根6082－T6型高强铝合金轴心受压构件进行数值模拟，并与试验结果进行对比分析.对影响有限元计算结果的各项因素，包括网格划分与尺寸、端板厚度、初弯曲大小和材料参数进行分析.有限元模型采用完全积分形式的20节点实体单元，铝合金应力应变关系采用Ramberg-Osgood模型.结果显示:采用三维实体单元C3D20进行的数值模拟与试验的屈曲荷载相对误差控制在12%以内;通常的轴向网格尺寸与端板厚度对构件稳定系数的影响可忽略不计，支座处端板的存在基本不会影响构件的铰支受力状态;稳定系数随初弯曲幅值的增大而降低，随材性参数n值的增大而提高;随着名义屈服强度f0.2的增大，构件的屈曲荷载也随之增大，且增幅在长细比λ越小时更为显著.

铝合金;轴压;数值模拟;稳定系数;屈曲

铝合金结构的发展始于20世纪30年代，以其高强、轻质、耐腐蚀等优点被广泛应用于建筑领域.但由于铝合金材料弹性模量较低，因此构件的失稳问题显得尤为突出.欧洲、美国于20世纪70年代各自建立了设计规范［1－2］，目前，我国刚刚推出铝合金结构设计规范［3］，然而针对部分型号铝合金的设计大多参考国外规范，其适用性仍有待研究.本文利用有限元软件ABAQUS对H型、箱型截面的6082－T6型高强铝合金轴心受压构件进行数值模拟，并与构件试验结果进行比较，对影响有限元计算结果的各项因素，包括网格的划分与尺寸、端板厚度、初弯曲大小和材料参数进行分析，提供了较为合理、有效的铝合金轴压构件的有限元数值模拟方法.

1 有限元模型

1.1 数值模拟流程

由于实际的铝合金构件并非理想直杆，为极值点失稳问题，影响其失稳模式的主要因素为初始缺陷，初始缺陷包括残余应力与初始弯曲，本文研究的挤压成型的高强铝合金构件，其残余应力很小，可以忽略不计［4－5］.初弯曲可以分解为无穷多种模态形状的组合［6］，但构件通常以一阶模态失稳为主.如果二、三阶模态为局部屈曲，则构件的失稳形式中还会伴随相应的局部屈曲.因此对各构件先按理想直杆进行模态分析，取其一阶模态形状并将其初弯曲幅值调整到L/1 000(L为构件长度)，如果二、三阶模态为局部屈曲形式，则初始缺陷中要相应引入局部屈曲模态，然后基于大变形理论进行非线性分析.对屈曲一类不稳定问题，当力－位移平衡路径出现下降段时，切线刚度变为负值，牛顿－拉普森迭代将出现收敛困难，因此多采用改进的牛顿－拉普森方法或弧长法［7］，本文采用的是弧长法，整个有限元屈曲问题求解流程见图1.

1.2 有限元模型的建立

Ramberg-Osgood模型是目前广泛使用的分析模型，且与本文研究的高强铝合金构件的材性本构关系曲线吻合较好，Ramberg-Osgood［8］模型的表达式为

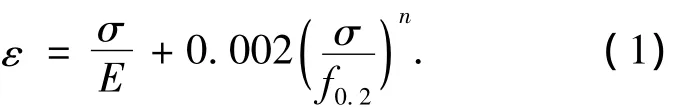
式中E与f0.2分别为材料的弹性模量与名义屈服强度，采用 Steinhardt［9］建议，取 n=f0.2/10，该值与本文铝合金试件的材性试验结果吻合较好.

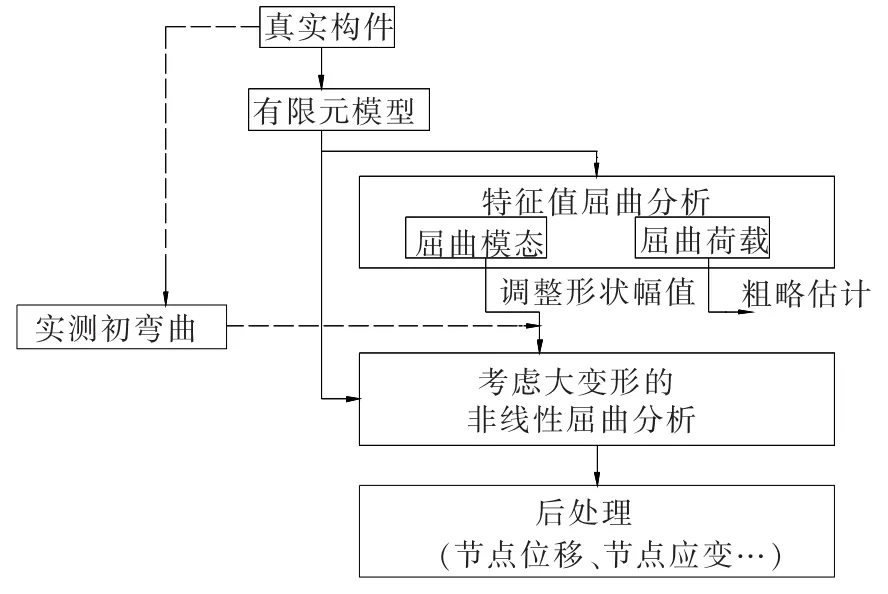
图1 数值模拟流程

采用三维实体单元进行有限元模拟，为避免线性单元模拟弯曲时单元刚度过大导致的剪力自锁，和采用减缩积分时积分点过少而产生的沙漏问题［10］，本文采用完全积分下的三维20节点二阶单元C3D20来模拟高强铝合金构件在轴心受压下的力学行为.

有限元模型中的单元类型、本构关系模型及6082－T6型铝合试件的材性试验参数见表1.

表1 有限元模型参数

本文涉及的所有试件皆在MTS电液伺服压力机上完成，试验时，构件两端各用一个钢板槽，通过向内浇注高强石膏将H型或箱型构件固定住，钢槽底面单向开槽，以模拟单向铰支，试件两端支座及试验装置见图2、3.位移计和应变片测点位置见图4、5.由于单向铰支构件的端部应力较小，石膏一般不会出现裂缝，因此在有限元模型中将试件端部的钢板及石膏简化为钢材质，并按线弹性体的应力－应变关系处理.

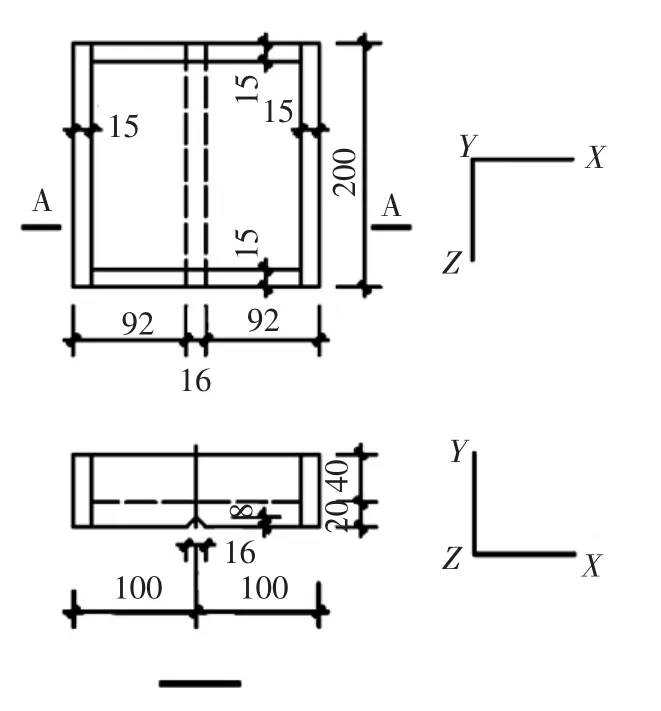
图2 带有单向刀口的钢板槽（mm）

图3 试验装置

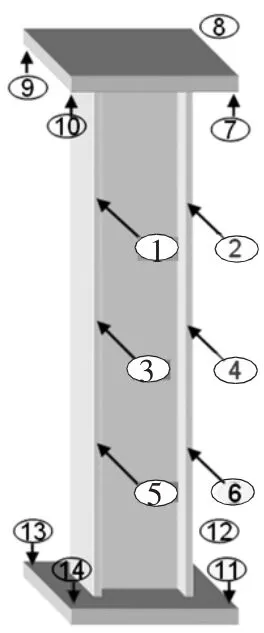
图4 位移测点

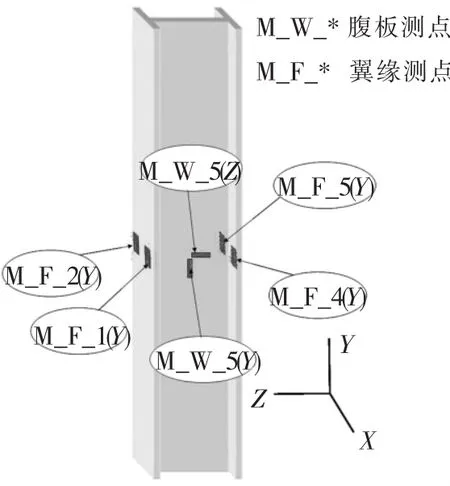
图5 应变测点

2 与试验结果对比

本文针对H型、箱型2种截面共17根试验构件［11］进行数值模拟.模拟所用构件长度均为实测值，因此对同一种名义尺寸的构件模拟结果略有差异，数值模拟与试验关于屈曲荷载及破坏模式的比较见表2.模拟结果显示:17根构件的破坏形式与试验结果一致，全部以整体弯曲失稳为主，其中箱型试件F1－1、F1－2和F1－3还伴随局部失稳现象.在数值模拟时，上述3个试件的二、三阶失稳模态为局部屈曲，因此在初始缺陷的引入中包括整体与局部屈曲2种形式，其中局部屈曲幅值 ωd采用 Walker［12］提出的公式

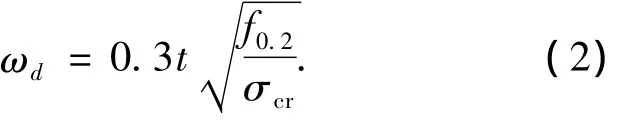
式中:t为构件截面厚度，σcr为弹性局部屈曲应力，可以通过模态分析得到.

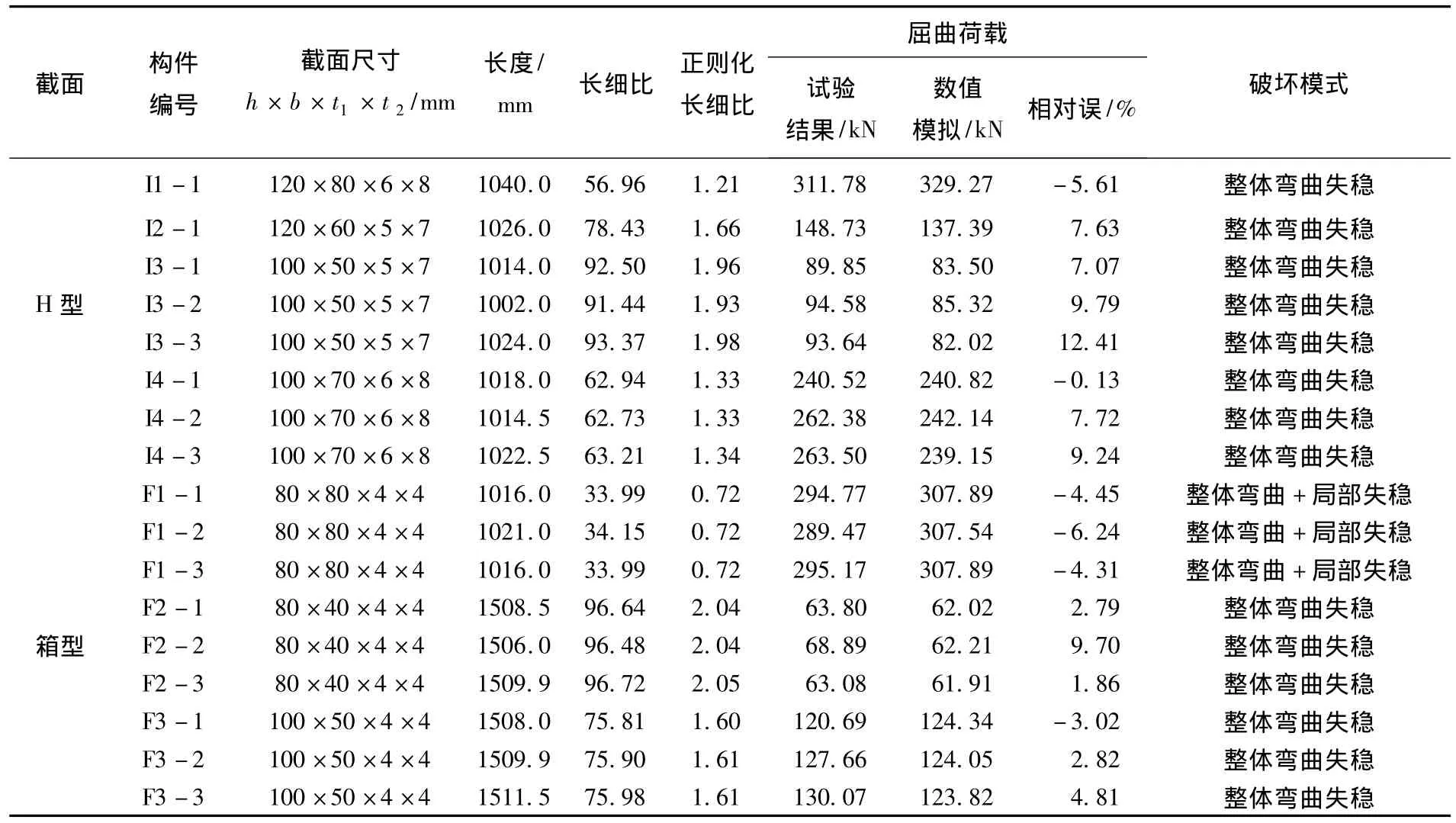
表2 数值模拟与试验结果屈曲荷载比较

由表2可知，试验与模拟结果关于屈曲荷载的相对误差控制在12.41%内.以构件I3－1为例，部分测点实测值与数值模拟的位移与应变结果见图6、7.数值模拟与试验结果的对比说明，两者在荷载－位移曲线以及试件局部测点的应变变化方面皆显示了良好的一致性，说明本文的铝合金轴压构件的数值模拟在单元选取、参数设置及网格划分等方面是适用的.

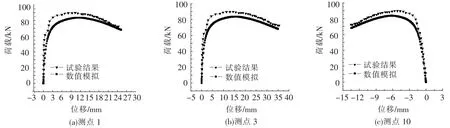
图6 试件I3－1荷载－位移曲线

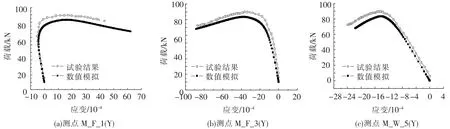
图7 试件I3－1荷载－应变曲线

3 有限元结果影响因素分析

3.1 网格划分及其尺寸

通常情况下网格尺寸越小，计算精度越高，但机时增加，为此进行了构件及支座端板的网格尺寸敏感性分析.考虑到铝合金构件腹板和翼缘的厚度很小，一般在10 mm以内，可将其在腹板和翼缘厚度方向上划分为2个单元，同时尽量保证构件横截面内(XZ平面，见图8)的单元格为正方形或接近正方形.另外，两端支座处端板上位于构件截面之外的网格对结果影响很小，可以采用较粗糙网格.为确定构件沿轴向(Y向)的网格尺寸，进行了稳定系数φ对网格尺寸的敏感性分析，稳定系数的计算公式为

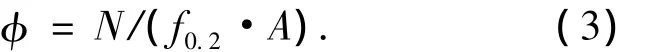
式中:N、f0.2、A分别为屈曲荷载、名义屈服强度、构件截面面积.

针对4种不同的长细比构件，沿构件轴向(Y向)的网格尺寸分别按 10、20、30、40、50 mm 计算了构件的稳定系数，结果见图9.构件稳定系数结果几乎不受轴向网格尺寸的影响，所有相对误差控制在0.05%以内.为减少计算时间，本文轴向网格尺寸采用50 mm.

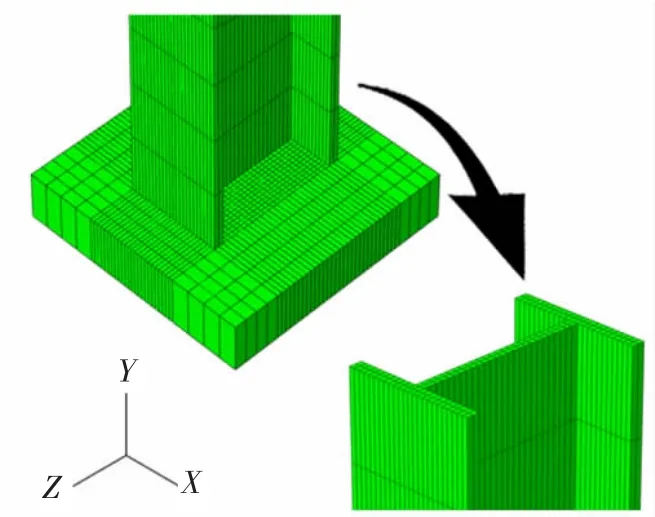
图8 有限元模型网格的划分

3.2 端板厚度

试验中通过石膏将构件固定在钢槽内，而在有限元模拟时将石膏与钢槽底板共同简化为钢材质的端板.试验中采用的钢槽底板与石膏的总厚度一般在40 mm左右，本文分析了上下刀口间距保持不变，但端板厚度分别为 0、10、20、30、40 mm 5种情况对φ的影响，结果见图10，其中端板厚度为0意味着理想铰支状态，可以看到，不同正则化长细比下数值模拟结果几乎不受端板厚度的影响，相对误差控制在0.8%以内，说明试验时采用的单向铰支座方法能够保证试件接近理想铰支状态，不会带来较大误差.

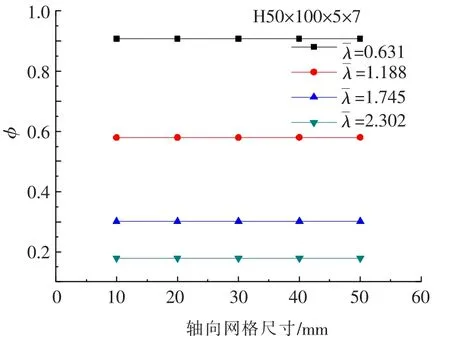
图9 轴向网格尺寸对稳定系数的影响

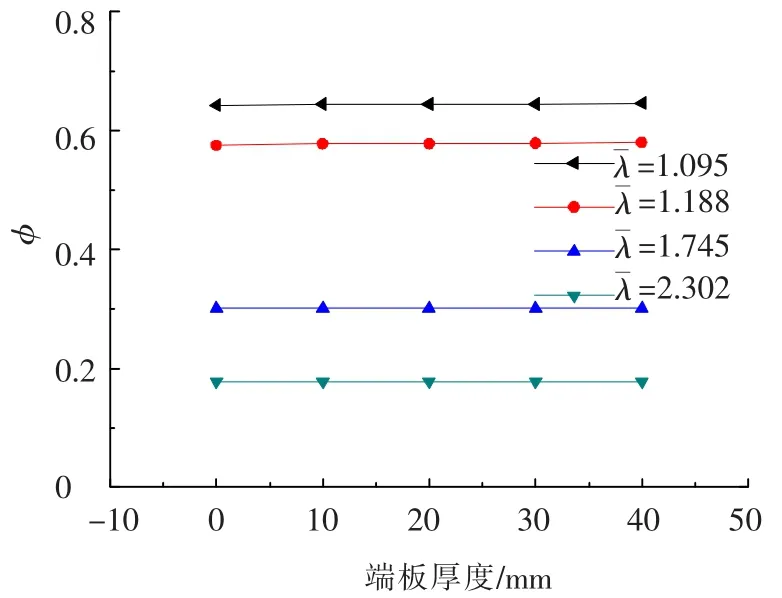
图10 端板厚度对稳定系数的影响

3.3 初弯曲大小

国内外规范针对铝合金轴心受压构件，均采用与Perry公式形式相同的设计公式［1－3］

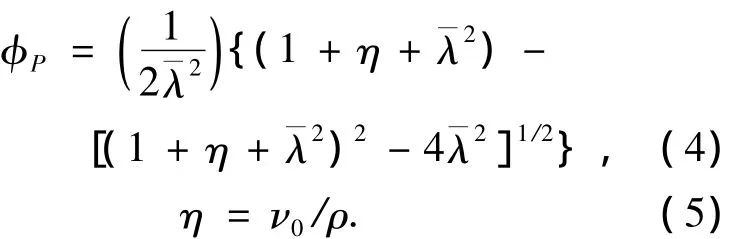
式中:φP为柏利公式推导的稳定系数;为正则化长细比为相对初弯曲;ν0为初弯曲幅值，一般表示为长度的函数，ν0=L/m，m为系数，例如中国钢结构设计规范中m取1 000;ρ为截面核心距.由于相对初弯曲η一般表示为长度的函数，即与正则化长细比有关，为方便进一步分析，将相对初弯曲作如下变换

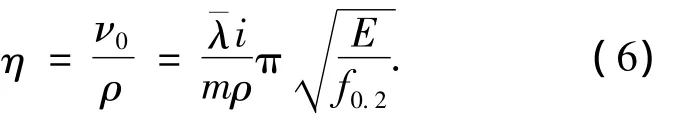
式中i为截面绕弯曲轴的回转半径.

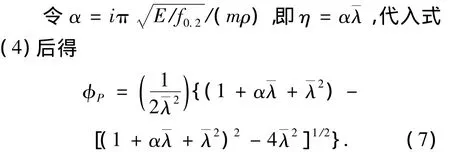
对式(7)和有限元模拟得到的稳定系数进行对比，见图11.

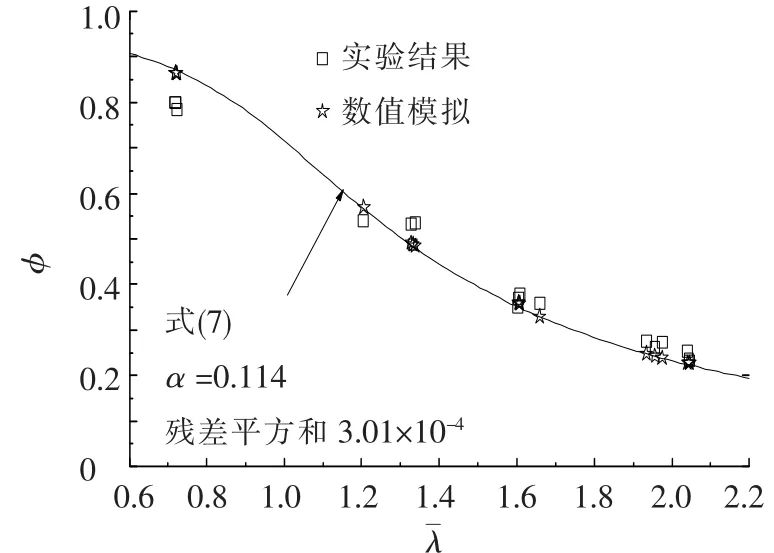
图11 试验、数值模拟结果与式(7)比较

为进一步验证本文数值模拟结果与柏利公式的一致性以及了解初始弯曲对有限元结果的影响，对式(7)中参数α求偏导数，α中包含了初始弯曲的因素，并引入参数K，得

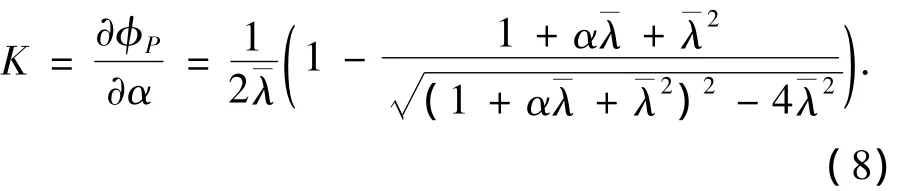
将式(8)用三维视图表示，见图12，此时α∈(0，1］，∈(0，4］，即属于通常的初弯曲与正则化长细比范围内.当α→0→1时，K的绝对值趋近于最大，即这种情况下利用柏利公式会得到最大的稳定系数.为验证数值模拟结果是否也存在此规律，对相同截面尺寸及不同长细比和初弯曲情况下的H型构件进行数值模拟，见图13，图中曲线表明:对同一长细比构件，稳定系数随初弯曲幅值增大而减小;当接近1时，初弯曲幅值对稳定系数的影响更明显，例如当=1.188时，稳定系数由0.672(ν0=L/8 000)降低至0.525(ν0=L/500)，降低了27.98%，因此初弯曲幅值对数值模拟结果的影响与理论推导类似.

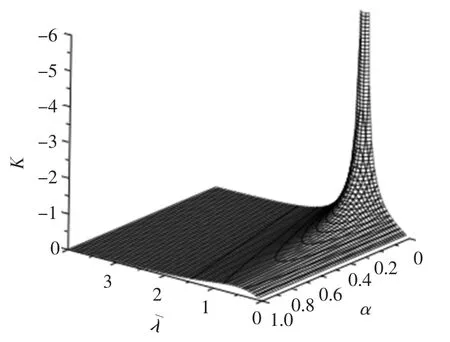
图12 初弯曲大小对柏利公式的影响

3.4 材性参数n和f0.2

本文应力应变关系采用Ramber-Osgood模型，如式(1)所示，并通过材性试验确定了式(1)中高强铝合金6082－T6本构关系中的3个参数，即弹性模量E、名义屈服强度f0.2和指数n.由于轴压试验构件的材料特性与材性试验试件之间存在差异，对本构关系中几个参数分别进行分析可以得到材料参数的影响规律，有利于分析误差产生的原因.从材性试验中了解到，构件的E一般比较稳定，因此材料的离散性主要反映在n与f0.2上.

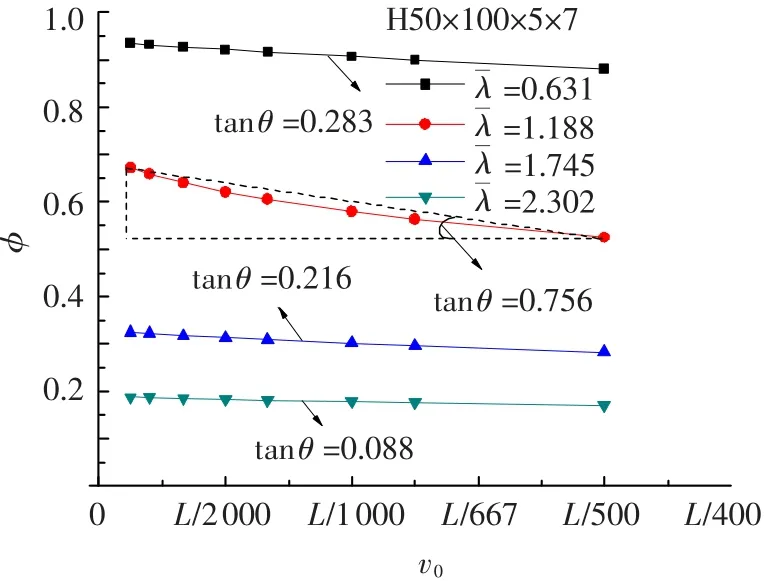
图13 初弯曲对稳定系数的影响

首先考虑f0.2不变，n值决定了图14中曲线的切线模量，当n值越大，本构关系模型越接近理想弹塑性，反之n值越小，本构关系模型越接近完全线弹性体，但同时弹性模量也大幅度降低.图14中，由于假定f0.2不变，应力应变曲线近似相交于应力值为f0.2处，各当应力小于f0.2时，n值越大，同一应变所对应的应力越大，即构件达到相同变形所需施加的荷载越大.而构件弯曲失稳时，屈曲荷载所对应截面上的最大应力一般小于f0.2，因此对同一几何尺寸构件，n值越大，屈曲荷载越大.同理，在荷载 －位移曲线的下降区段，n值越大，同一变形所对应的荷载越小，即荷载下降越快.本文进行了构件在通常的n值范围(n=10～50)情况下的数值模拟，见图15.对同一构件，随n值增大，稳定系数略有增加，当接近1时，n值对稳定系数的影响更明显，例如当=1.188时，稳定系数由0.555(n=10)提高到0.586(n=50)，增长了5.51%.

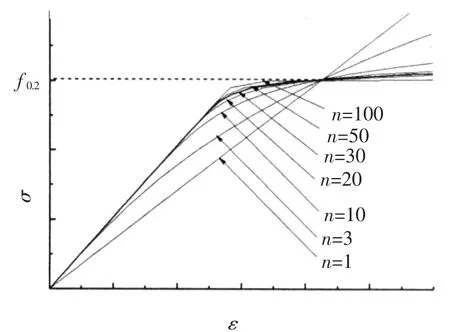
图14 指数n值对应力应变曲线的影响

6082-T6材料的f0.2一般为270～350 MPa，在弹性模量保持不变的情况下，f0.2的增加意味着本构曲线中弹性段的增长，见图16.本文针对4种长细比构件在不同f0.2情况下进行数值模拟，f0.2对屈曲荷载的影响见图17，可以看到，对λ相同的构件，屈曲荷载随f0.2增大而增大，且屈曲荷载的增幅随λ的减小而增大，例如当λ=108.82时，屈曲荷载从60.78 kN(f0.2=270)提高到了61.78 kN(f0.2=350)，仅提高了1.64%，而当λ=29.84时，屈曲荷载从278.07 kN(f0.2=270)提高到了355.54 kN(f0.2=350)，增长了27.86%.

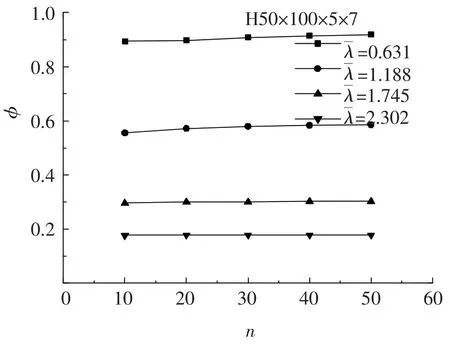
图15 指数n对稳定系数的影响

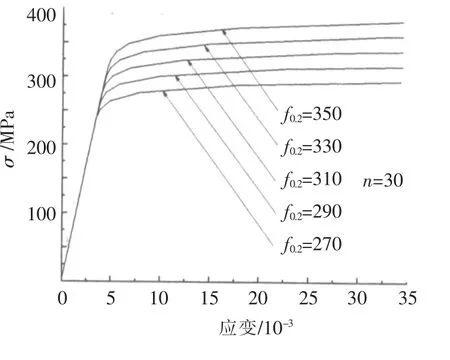
图16 f0.2对应力应变曲线的影响

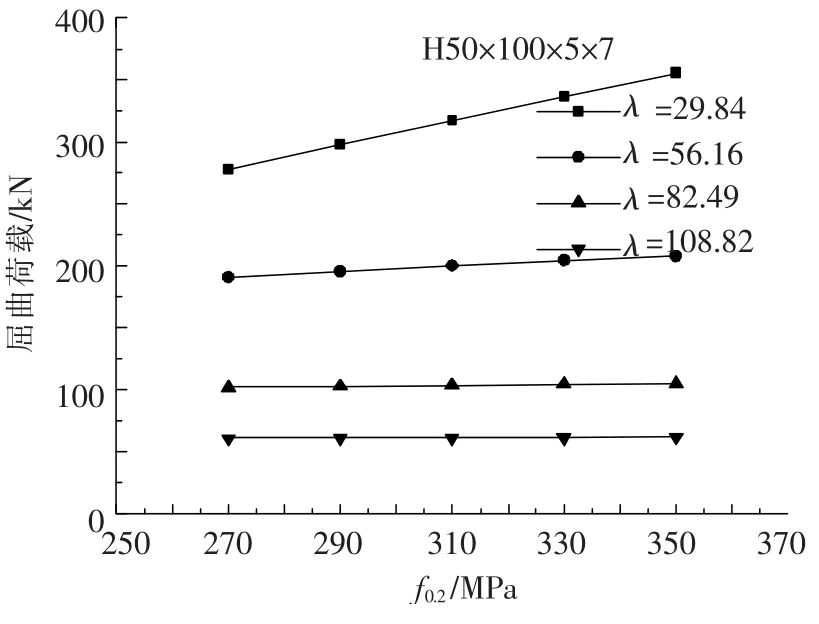
图17 f0.2对屈曲荷载的影响

4 结 论

1)采用3维实体单元C3D20模拟两端单向铰支H型及箱型高强铝合金轴压构件，其有限元结果在构件变形曲线及屈曲荷载方面与试验实测值吻合良好，最大误差控制在12%.

2)轴向网格尺寸和端板厚度对构件的稳定承载力结果影响很小，可忽略不计.

3)试验时采用的钢板槽与石膏结合的单向铰支座方法能够保证试件接近理想铰支状态，不会带来较大误差.

5)随着Ramber-Osgood模型中的材性参数n的增大，构件的稳定系数有所提高，且提高程度在为1.0时最为显著，约为5.5%;随着f0.2的增大，构件的屈曲荷载也随之增大，且增幅在λ越小时越显著.

［1］Eurocode 9:BS EN1999-1-1.Design of aluminum structures-general structure rules［S］.Brussels:European Committee for Standardization，2007.

［2］The Aluminum Association.Specification for aluminum structures［S］.6thed.Washington D C:The Aluminum Association，1994.

［3］GB50429铝合金结构设计规范［S］.北京:中华人民共和国建设部，2007.

［4］MAZZOLANI F M.Residual stress tests on French profiles 63×63×4 in aluminum alloys，Doc 16-74-3［R］.Brussels:ECCS Committee，1974.

［5］MAZZOLANI F M.Residual stress tests alu-alloy Austrian profiles，Doc 16-75-1 ［R］.Brussels:ECCS Committee，1975.

［6］陈骥.钢结构稳定理论与设计［M］.2版.北京:科学出版社，2003.

［7］ABAQUS analysis user's manual:version 6.9.1［M］.［S.l.］:ABAQUS Inc，2009.

［8］RAMBERG W，OSGOOD W R.Description of stressstrain curves by three parameters，NACA TN-902［R］.Washington D C:National Advisory Committee for Aeronautics，1943.

［9］STEINHARDT O.Aluminum constructions in civil engineering［J］.Aluminum，1971，47:131－139.

［10］庄茁，张帆，岺松.ABAQUS非线性有限元分析与实例［M］.北京:科学出版社，2005.

［11］ZHAI Ximei，WANG Yujin，WU Hai，et al.Research on stability of high strength aluminum alloy columns loaded by axial compressive load［J］.Advanced Materials Research，2011，168/169/170:1915 －1920.

［12］WALKER A C.Design and analysis of cold-formed sections［M］.New York:Wiley，1975.

Stability research and numerical simulation of high-strength aluminum alloy column in compression

ZHAI Xi-mei，WU Hai，WANG Yu-jin，FAN Feng

(School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China，xmzhai@hit.edu.cn)

To provide reliable verification and guidance for experiments，numerical simulations of 17 highstrength aluminum alloy columns in compression were conducted using ABAQUS and the results were compared with experimental results.Factors which influenced simulation results，including meshes size，thickness of end plates，initial imperfection and material properties were analyzed.3D full integration continuum element C3D20 and Ramberg-Osgood model for stress-strain relationship were adopted in simulation.The simulation results show that the relative errors of buckling load between experiments and simulations are under 12%;the meshes size and thickness of end plates have a negligible influence on stability coefficient，and the existence of end plates rarely influence mechanical properties of specimens with hinge supports;as initial geometric imperfection ascends and the parameter n of aluminum alloy descends，the value of stability coefficient decreases;buckling loads of specimens obviously increases as proof stress f0.2increases，especially for specimens with small slenderness ratio.

aluminum alloy;compression;numerical simulation;stability coefficient;buckling

TU395

A

0367－6234(2011)12－0001－06

2010－11－18.

国家自然科学基金资助项目(51108126).

翟希梅(1971—)，女，副教授;

范 峰(1971—)，男，教授，博士生导师.

(编辑 赵丽莹)