在高等数学教学中引入数学建模思想的探索与实践

李长青，吴伟志，张野芳

(浙江海洋学院数理与信息学院，浙江舟山 316004)

高等数学是大学理工科各专业的一门重要基础课，在学生素质的培养以及学生思维能力的培养方面有着不可替代的作用，它同时也是研究其他学科的一个有力工具.一个现代大学生如果具备良好的数学素养，能够将数学思想应用于解决实际问题，这对于其在专业方面的发展是非常有帮助的.

目前大多数高等院校高等数学教学采用的还是传统的教学方式，以教师为中心，重视理论的推导，而对数学的应用则没有给予充分的重视，在教学中不能把教学内容与解决实际问题联系起来，难以使学生体会到数学的威力，导致学生对学习高等数学毫无兴趣，严重影响了高等数学的教学质量.

数学建模是将数学应用于实际的必由之路，是联系数学理论与客观现实的桥梁.数学建模的过程,实际上就是把数学应用于实际的过程，在这一过程中能充分展示数学思想和数学方法的作用.在高等数学的教学过程中有意识地介绍一些建模方法和建模案例，通过这些例子，向学生展示如何将一个实际问题抽象化，从而用数学方法求解的全部过程.这对于学生数学思想的培养和数学应用能力的提高都具有促进作用，也是增强学生对数学的兴趣、提高学生学习高等数学的积极性、提高高等数学教学质量的重要手段之一.

1 将数学建模思想融入高等数学教学中

在高等数学教学过程中引入数学建模要采取循序渐进，逐步深入的原则，从简单的模型开始，由浅入深地展示数学建模的思想和方法.由于高等数学的教学对象是大学一年级学生，数学基础还很有限，所以数学建模的例子开始不应过难.在教学过程中我们采取了从初等数学的应用开始，随着教学内容的深入而逐步加深的方法引入数学建模案例，使学生在高等数学学习中看到数学在解决实际问题中的作用，提高了学生学习高等数学的兴趣和积极性，取得了良好的教学效果.以下是我们在教学过程中引入数学建模的具体做法.

1.1 利用初等数学建模

高等数学第一章的内容与高中阶段学生所学过的内容大同小异，学生对有些内容非常熟悉，如数列、函数的定义、几类初等函数的特性等.在这部分内容的教学中，教师可以引导学生利用初等数学的有关知识解决身边的一些实际问题.例如，利用数列的有关知识分析购房贷款的分期付款问题[1]，利用指数函数对生物种群的增长进行预测等[2].通过这些问题向学生介绍数学模型构建的以下几个步骤：(1)分析、识别问题，抓住问题的主要矛盾，列出问题中所包含的变量；(2)分析这些变量，对这些变量间的关系作出初步假设；(3)寻求一个满足上述关系的函数或图形，必要时通过计算机对所掌握的数据进行绘图，然后根据图形寻求符合要求的函数关系；(4)对模型进行检验，分析误差的具体情况，必要时对模型进行改进.

在第一章的教学中我们采用了如下的例子[2].在使用地高辛治疗心脏病的过程中，医生必须使开出的处方用药量能保持患者血液中地高辛的浓度高于有效水平而不能超过安全用药水平.通过具体测量得到的数据见表1.

其中x表示用了初始剂量后的天数，y表示病人血液中剩余地高辛的含量，初始剂量为0.5 mg.利用以上数据构建血液中地高辛含量和用药后天数间关系的数学模型，并预测用药12 d后血液中地高辛的含量.

为了得到x与y之间的关系，先用数学软件MATLAB在坐标系中作出所给数据(x，y)的散点图(图1)，由指数函数的图形知，这些点大致地在一条指数曲线上.为了验证这一点，考虑地高辛在血液中的衰减率，将后一天病人血液中剩余地高辛含量除以前一天的剩余含量，得到如下数据：

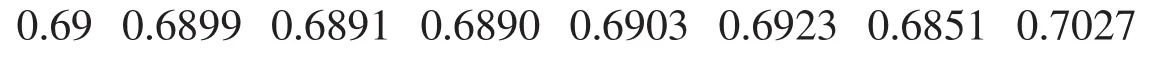
由此知，后一天病人血液中剩余地高辛含量平均是前一天的剩余含量的0.691 05倍，从而，x与y之间的关系可以用指数函数来描述，由于初始剂量为0.500 0，故可得y=0.500(0.61905)x=0.5000e-0.3695x将以上函数的图形和前面的数据散点图重叠起来(图2)，由图形可以直观地看到，该指数函数能够很好地描述x与y之间的关系，进一步还可以通过分析误差来看用以上函数关系来预测患者血液中地高辛含量的结果是否可信，分析结果见表2.

表1 血液中剩余地高辛含量Tab.1 Digoxin content in blood

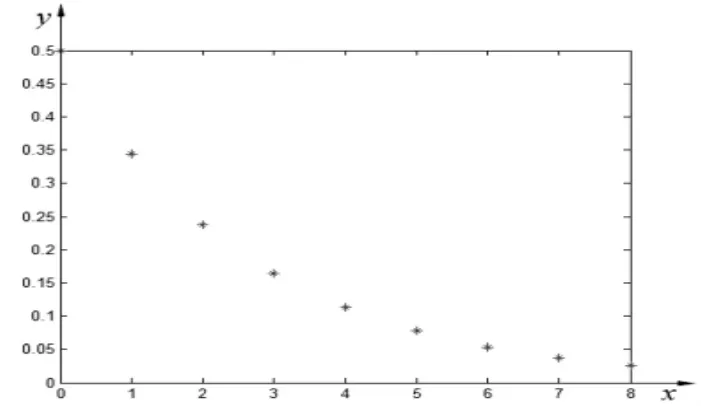
图1 地高辛含量散点图Fig.1 Scatter diagram of digoxin content

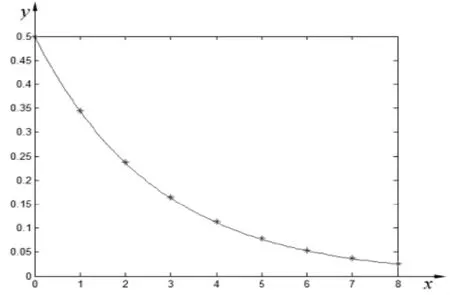
图2 地高辛含量拟合曲线Fig.2 Fitting curve of digoxin content

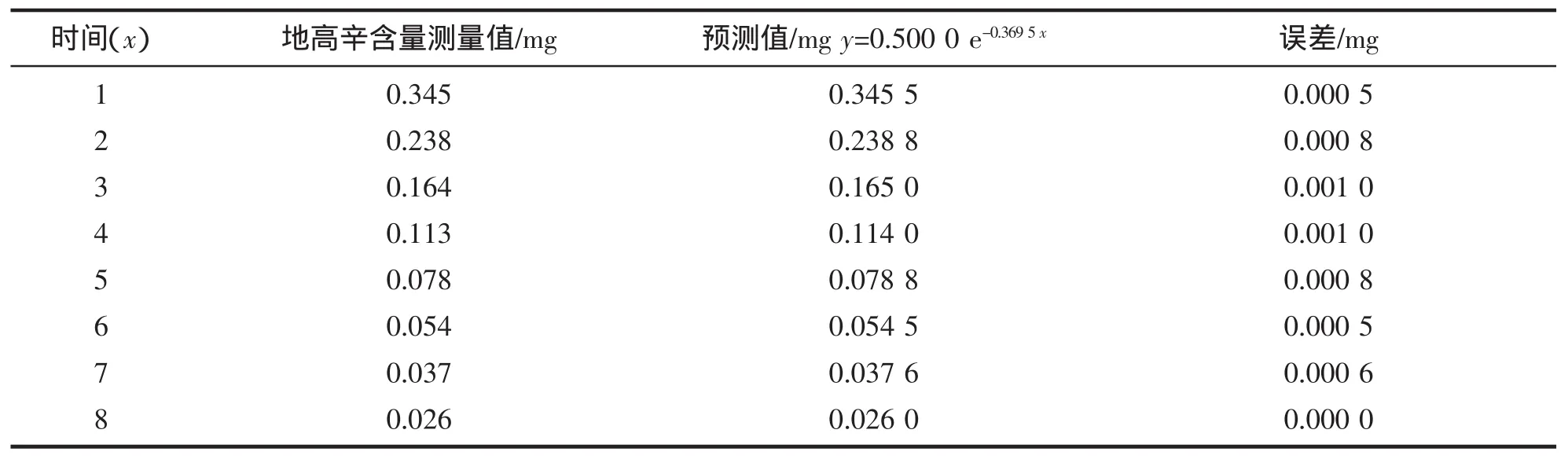
表2 误差计算表Tab.2 Error calculation table

从表2可以看出，预测值和实测值间的误差非常小，利用我们得到的关系来预测血液中的地高辛含量是可信的.利用以上关系式可得12 d后血液中地高辛的含量为y(12)=0.005 9 mg.

将初等数学用于解决实际问题进行建模的情形非常多，如生产企业的库存问题、有价证券的贴现及经验公式的建立问题等[2-4].

1.2 利用高等数学建模

随着高等数学课程教学的深入，学生所掌握的数学知识逐渐增加，数学建模的例子也可以逐渐加深.在讲完导数与微分后可以在授课中加入关于最优化问题的数学建模，例如，可以利用求函数的最大值与最小值研究零售商店存货成本最小问题、生产企业平均成本最小问题、利润最大化问题及饮料易拉罐的形状设计问题等.通过这些具体问题引导学生分析问题，利用所学数学知识建立合理的模型，使学生体会到数学在各个领域中的重要性.在多数数学建模问题中都离不开微分方程，如简谐振动问题、降落伞的运动规律、机场跑道长度的设计、铁轨弯道处缓和曲线的设计及种群增长问题等.在微分方程内容的讲授中可以精选几个作为建模例子，通过这些数学建模问题进一步阐明数学建模的思想和方法.

逻辑斯谛方程在许多领域中有着广泛的应用，新商品的销售规律、树木生长规律及人口增长规律等，都可以用逻辑斯谛方程来描述[2].在将一阶微分方程的求解方法介绍给学生后，我们对人口增长数学模型进行了分析.

1.2.1 人口增长模型

人口的增长受多种因素的影响，诸如人口基数、出生率和死亡率、工农业生产水平、医疗水平、环境状况等.如果只考虑影响人口增长的主要因素—增长率及人口基数，利用导数是函数的变化率这一事实，引导学生按下述方式建立人口增长模型.设P(t)，r(t,P(t))分别表示t时刻的人口总数和增长率，则在t到t+△t这段时间内人口总数增长为

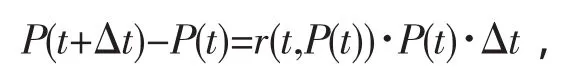
在上式两端同除以△t，并令△t→0，有

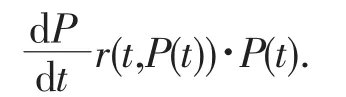
如果象[1]中假设人口增长率是一个常数，令r(t,P(t))=r(常数)，则得如下数学模型：

该公式在很长的一段时间内能够比较准确地反映世界人口总数的变化规律，如1980年的世界人口总数按上述公式计算为44.7459亿，而实际人口数为44.54亿，两者非常接近.但是，当时间跨度再增大时，上述公式与实际情况的差距就会明显地增大.按上述公式，2010年的世界人口总数为81.53亿，而实际统计2010年世界人口总数为69.09亿，这两者之间相差就非常大.另外，当t→∞时，P(t)→+∞.这说明对于大跨度时间利用上述公式来预测人口总数是不正确的.通过对上述建模过程进行分析可以看到，假设人口增长率为常数显然不合理.如前所述，人口的增长受众多因素的影响，随着人口的增加，由于环境、经济等因素的影响，相对增长率会逐渐减少，这可以从下述统计资料得到证实.

由表3可以看出，在1990-1999年间增长率平均每年大约减少0.000 36%，因此可以取r(t,P(t))为P(t)的线性函数试探建模.设r[P(t)]=r+bp(t)，r称为固有增长率，并且存在一个数值M使得r(M)=0.由以上假设可求得r(P)=r(1-P/M)，最后得到新的人口增长数学模型

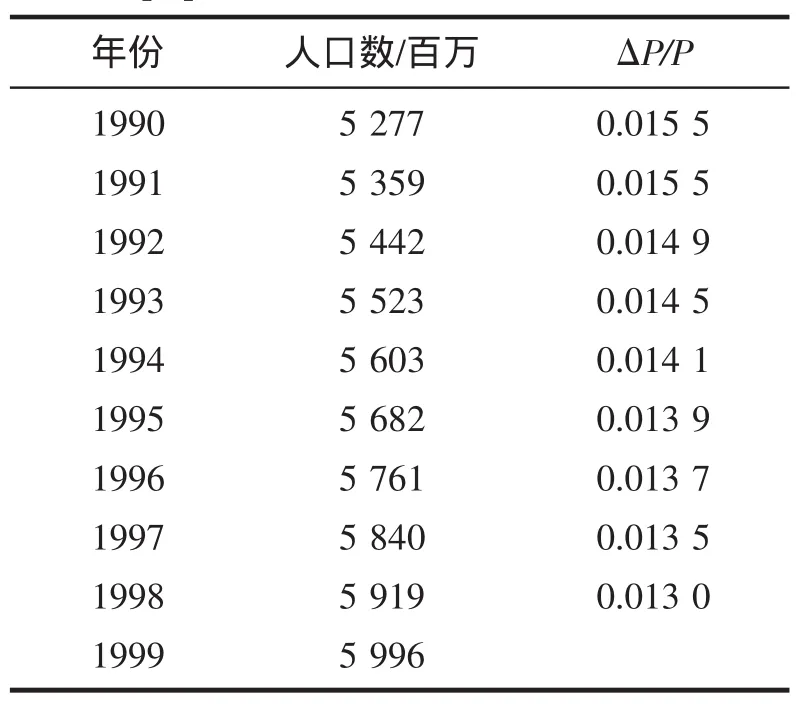
表3 1990-1999世界人口增长率Tab.3 Growth rate of world population within 1990-1999

该模型称为逻辑斯谛(Logistic)模型，由荷兰生物学家Verhulst于1837年首先给出.它的解为

其中M为最大人口数，也称为承载容量，从长远来看，这是环境所能够支撑的最大人口数.由公式(5)可以看出以下几点：

(i)若 r＜0，t→∞，P(t)→0；

(ii)若 r＜0，对于任意的 P0，当 t→∞ 时，有 P(t)→M；

(iii)若r=0，即增长率保持为0，则人口总数也不变，即P(t)=P0.

据生物学家估计，r的自然值为0.029，我们根据1961年世界人口总数为30.60亿及1990年的世界人口为52.77亿，可以算得M=117.12亿.

最后对上述模型进行检验，先用MATLAB做出(5)的图像(以1961年作为t=0)，再把1995，1997，1999年的世界人口总数在同一坐标系中画出，另由统计资料知2003，2008，2010年世界人口分别为63.01，67.44，69.09亿，把这3组数据也绘制在上述坐标系中(图3).由图3可以看出，(5)式能较好地描述世界人口总数随时间变化的规律.由此我们可以预测2020年世界人口总数为

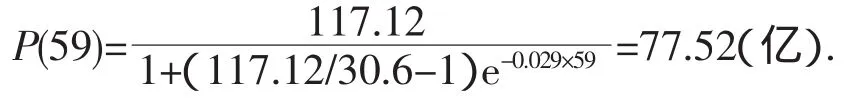
随着科学技术的发展和进步，人类可以改善自己的生存环境，上面我们提到的所谓最大承载量也会发生变化.在上面的建模问题中并没有考虑这个因素，随着人类文明的发展，上述模型也会慢慢变得不能够正确地反映世界人口的变化规律，要得到更加符合实际的数学模型，需要考虑更多的影响人口增长的因素，重新进行数学建模，相应地问题也会变得比较复杂.

应该指出的是，反映实际问题的数学模型大部分是很复杂的，不容易甚至不可能得到精确解，而从实际应用的角度来看，只需要在工程技术精度要求范围内求解即可.因此，在数学建模过程中需要对所考虑的实际问题进行合理的简化，抓住主要矛盾，忽略次要矛盾，这也是数学建模的一个基本原则.

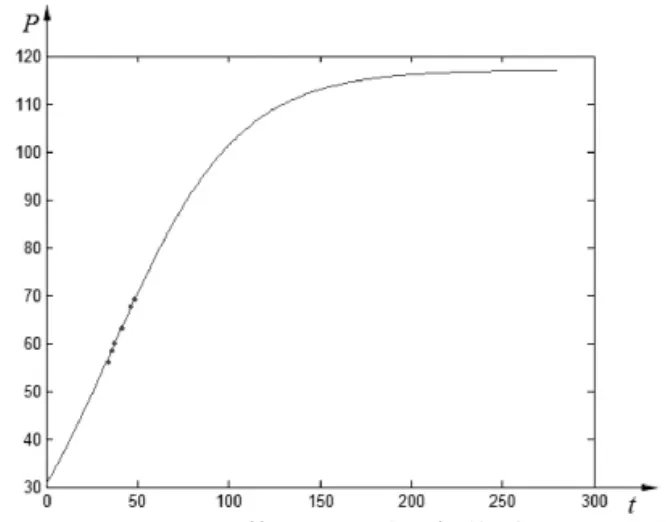
图3 世界人口拟合曲线Fig.3 Fitting curve of world population

1.2.2 火车弯道缓和曲线的设计问题[4]

火车在弯道上行驶时会产生离心力F=mv2/R，在修筑铁路时，常需根据地形特点和最高限速的要求来设计铁轨的圆弧弯道.如果火车由直道直接转入圆弧弯道，由于在直道与圆弧弯道衔接处轨道曲线的曲率由零突然改变到1/R，列车所受到的离心力也由零突然改变到F，这会使列车产生振动，严重时可导致车辆和轨道的损坏.为了行驶平稳，往往在直道和圆弧弯道之间接入一段缓冲段OA(图4)，使轨道曲线的曲率由零连续地过渡到圆弧的曲率1/R，列车所受到的离心力也由零均匀地逐渐增加到F，其中R为圆弧轨道的半径.所加的曲线称为缓和曲线，求它的方程.

首先建立坐标系如图4所示，设铁轨直道沿负半x轴直到坐标原点，从第一象限中的A点处开始是半径为R0的圆弧，OA是所求的缓和曲线，OA的长度为l0.当列车匀速行驶时，由F=mv2/R知，要使离心力均匀变化，只需缓和曲线的曲率K=1/R均匀变化.取OA的曲率与从原点开始的弧长l成正比即可达到上述要求，令K=Cl，由K(l0)=1/R0，可求得C=1/(R0l0).从而缓和曲线的曲率为

设缓和曲线的方程为y=y(x)，由曲率及弧长的计算公式可得，

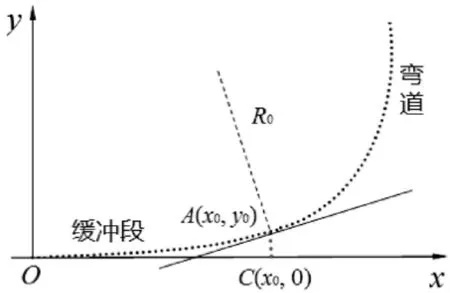
图4 铁轨缓和曲线Fig.4 Easement curve of rail way

上式就是缓和曲线应满足的方程.由于这是一个积分微分方程，求解困难，所以，考虑缓和曲线应满足的参数方程.

由此得到缓和曲线以弧长l为参数的参数方程

将α也用l表示，由曲率的定义知，K=dα/dl，再由(6)式可得

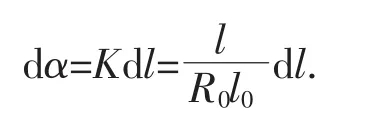
由题设知α(0)=0，积分上式可求出

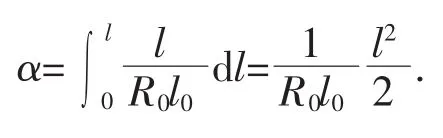
将其代入(8)式中，有

上式中的两个积分都积不出来，由它们所确定的关于x，y的微分方程也不能通过积分求解.利用泰勒展开式求解上述积分，把(9)中的被积函数展开成泰勒级数

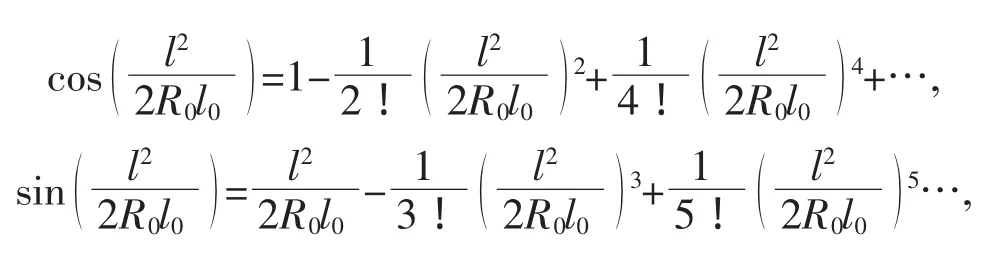
最后积分得到

在缓和曲线长度不大的情况下，上式右边的级数收敛速度很快，如果只取级数的第一项，就有

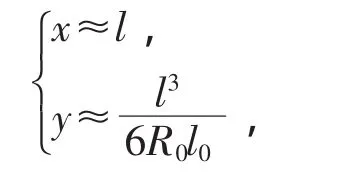
2 几个值得注意的问题

从微积分的发展历史可以看到，在极限、导数、微分、积分等概念的形成过程中无不体现着数学建模的思想，所以，在高等数学教学过程中随着概念的引入而增加数学建模的例子也是很自然的.从我们的教学实践来看，通过适当引入建模案例可以使一些比较复杂的数学概念变得直观且易于理解，同时使学生感受到数学在解决实际问题中所发挥的巨大威力.引入建模案例可以有效地提高学生学习高等数学的兴趣和积极性，能够有效地提高学生的数学素养.引入建模案例也增强了学生分析问题、解决问题的能力，对高等数学教学质量的提高是非常有帮助的.对理工科各专业来说，高等数学是一门基础课，因此在具体的教学实践中还应注意以下几个问题：

1)对任课教师的要求.将数学建模问题融入到高等数学的教学中要求任课教师具备解决实际问题的能力，要求教师了解一些相关专业知识，充分了解数学在不同专业中的应用情况，具备较宽的知识面，从学生所熟悉或将来要从事的专业问题中提炼应用案例.此外，数学教师应掌握一些数学软件，能够将其运用于高等数学的教学中，特别是利用数学软件的计算能力和绘图能力将抽象数学问题直观化.

2)任课教师要把握好引入建模例子的时机.在授课过程中，任课教师要根据课程的进展情况，依据各章的具体内容选取与教学内容相匹配的建模案例，循序渐进，让学生从建模问题中了解高等数学的具体应用，引导学生用数学方法解决实际问题.

3)解决好基本理论与应用问题之间的关系.在教学过程中应该切记，高等数学是基础课，不能把它当作数学建模课来讲授，要保证完成高等数学教学大纲所规定的教学内容.数学建模的例子要精选，难度要适合大一学生的水平，重点在于把数学建模的思想方法展示给学生，使之在教学过程中能够产生画龙点睛的效果.

[1]叶其孝.把数学建模的思想和方法融入大学数学课程要从一年级开始 [C]//大学数学课程报告论坛组委会.大学数学课程报告论坛文集2009.北京:高等教育出版社,2010.

[2]SMITH R T,MINTON R B.Calculus[M].第2版.北京:高等教育出版社,2004.

[3]FINNEY R,WEIR M,GIORDANO F R.托马斯微积分 [M].第10版.叶其孝,王耀东,唐 兢,译.北京:高等教育出版社,2003.

[4]贾晓峰.微积分与数学模型[M].北京:高等教育出版社,2008.

[5]同济大学数学系.高等数学[M].第6版.北京:高等教育出版社,2007.