电动汽车复合制动系统状态估计控制算法

刘清河，刘 涛，孙泽昌

(1．哈尔滨工业大学(威海)汽车工程学院，264209山东威海，qingheliu@sina．com;2．同济大学汽车学院，201804上海)

电动汽车复合制动系统状态估计控制算法

刘清河1，刘 涛1，孙泽昌2

(1．哈尔滨工业大学(威海)汽车工程学院，264209山东威海，qingheliu@sina．com;2．同济大学汽车学院，201804上海)

针对目前再生制动静态分配控制策略存在的问题，提出了基于复合制动系统结构的行车状态参数估计算法，并利用建立的硬件在环仿真环境仿真验证了算法对参数估计的效果．提出了基于行车状态估计的最高能量回收控制策略优化算法，仿真分析了算法优化前后的控制过程和效果．硬件在环仿真数据表明，优化后的策略有效提高了能量回收效率，防止了车轮的提前抱死．

新能源电池汽车;复合制动;路面附着系数;状态估计

目前，国内外研究机构对复合制动技术已进行了多年研究［1－7］．新能源车辆的复合制动系统主要分为两种型式:电液并行复合制动系统和基于线控制动的电液串行复合制动系统［2］．这两类复合制动系统均是在以一定的制动力分配算法控制下优先施加再生制动力，然后根据需要施加机械摩擦制动力［4］．复合制动控制算法的优劣在很大程度上决定了复合制动系统的性能．目前，广泛采用的复合制动控制算法主要有两种:再生制动力与机械摩擦制动力并行施加的并行复合制动控制算法和先施加再生制动，后施加摩擦制动的串行复合制动控制算法．文献［ 2，5］对以上算法的具体实施手段进行研究，但均局限于前后车轮静态制动力分配状态上，对动态过程分析较少．在这种控制策略下，新能源车辆施加再生制动力后，驱动轮抱死趋势增加，因此，如何避免新能源汽车复合制动系统驱动轮过早抱死成为复合制动系统技术难点之一［6－7］．

本文将车辆行驶状态估计与复合制动控制策略相结合，建立一种以车辆行驶状态估计结果为参数的动态复合制动控制策略，在避免驱动轮过早抱死的情况下有效利用地面的附着能力和再生制动系统性能．

1 行车状态参数估计算法

复合制动系统制动时的典型特点是在驾驶员制动操作的初始阶段总制动力需求较低而存在一定的纯再生制动阶段，在此阶段仅存在驱动轮再生制动力，非驱动轮处于纯滚动状态．复合制动系统的这一结构特点为行车状态参数估计提供了结构便利．

复合制动控制算法中所涉及的行车状态参数主要有两类:路面状态参数(即路面峰值附着系数φbmax)和车辆结构参数(如整车质量、质心位置、轴距、滚动半径等).对于所研究的轿车而言，车辆结构参数除整车质量外，其余参数变化范围较小.因此将整车质量m和路面峰值附着系数φbmax作为行车状态估计的主要任务.

在纯再生制动阶段，对车辆及其前轮(驱动轮)做受力分析，如图1所示．

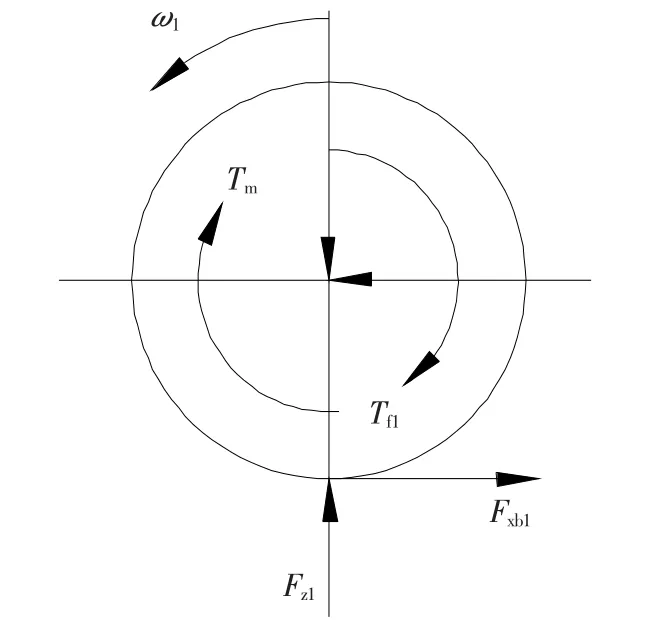
图1 纯再生制动轮受力图

则:

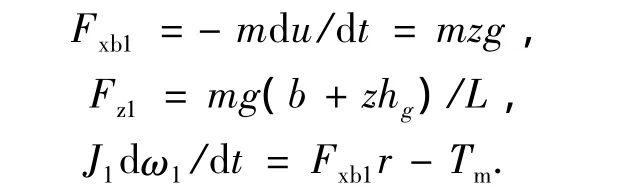
式中，Fxb1、Fz1分别为前轮地面制动力和前轴载荷，m为整车质量，u为车速，z为制动强度，hg、b分别为质心高度和质心到后轴的距离，J1为前轮转动惯量，ω为前轮转速，r为滚动半径，Tm为再生制动力矩.

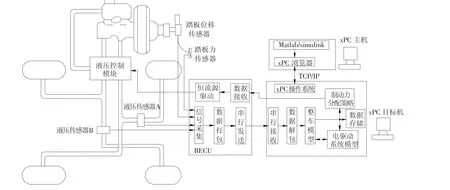
图2 复合制动系统硬件在环仿真试验平台

由于此阶段滑移率小，仍然处于线性阶段［8］，在汽车轮胎模型的线性区，路面附着系数φb线性段的斜率与路面峰值附着系数φbmax具有良好的线性关系，因此

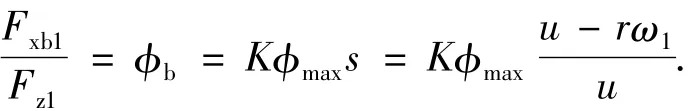
整理成最小二乘法辨识的基本形式，得

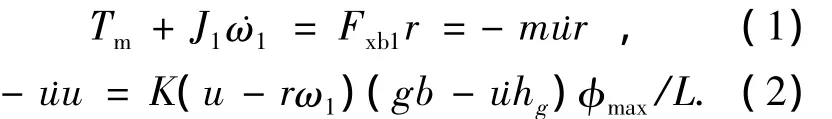
令y=Tm+J1˙ω，x=－˙ur，则式(1)可以写成最小二乘法系统辨识的标准模型形式y=mx.根据最小二乘法系统辨识理论，参数m的估计值)m的递推辨识过程可以用下面的公式表示:

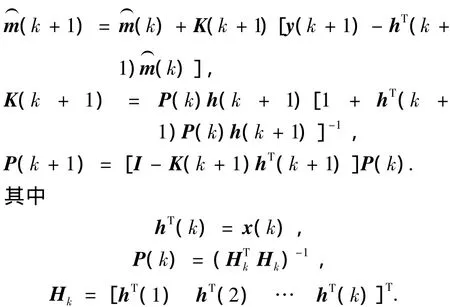
同理可将式(2)变换，列出φmax的递推最小二乘辨识算法.

2 行车状态参数估计算法仿真

为了研究和测试复合制动系统控制算法及其性能，作者在文献［9］和［10］中研究建立了复合制动系统硬件在环仿真试验平台，平台基本构成如图2．

试验系统主要由3个部分组成:xPC主机、xPC目标机和在环硬件，其中在环硬件包括液压控制模块、复合制动电子控制器、制动系统组件．液压控制模块采用反比例溢流阀组建立，电子控制器采用数字式PID电流闭环控制方式．制动系统采用超越3号制动系统．其中虚拟硬件主要包括整车模型、轮胎模型、锂离子蓄电池模型和电机及控制器模型4个部分，对于模型的关键部分:锂离子蓄电池模型和电机控制器模型均根据大量的实验数据建立［11］．

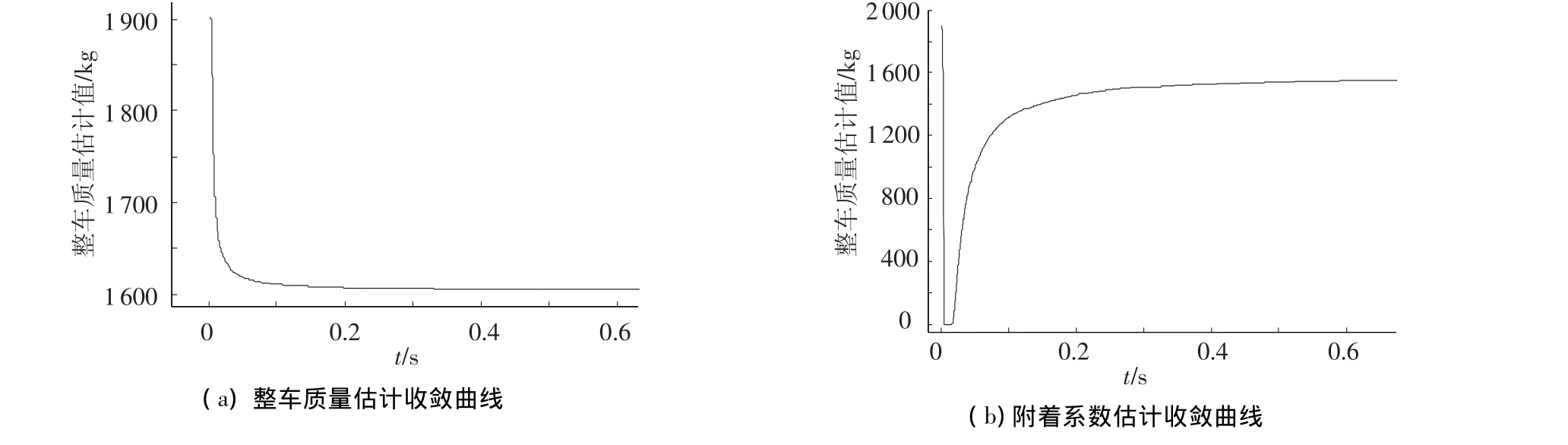
图3 高附着系数路面参数估计过程

将算法植入复合制动系统仿真模型中，通过改变仿真参数考察辨识的准确性．参数递推的初始值m设定为满载质量1 900 kg，路面峰值附着系数为φbmax=0.7.

经过设置不同的系统参数，对在线估计算法进行仿真．设定 m=1 600 kg，φbmax=0. 8，仿真得到参数递推辨识过程如图3所示.m估计值为1 606 kg，φbmax的估计值为 0. 81，误差分别为0.37%和1.25%.

设m=1 200 kg，φbmax=0. 3，仿真得到参数递推辨识过程如图4．m估计值为1 205 kg，φbmax的估计值为0. 302，误差分别为0.4%和0.6%．

可以看出，在采用模型仿真中的数据进行在线估计时，估计算法能很快收敛到真值，算法切实有效．

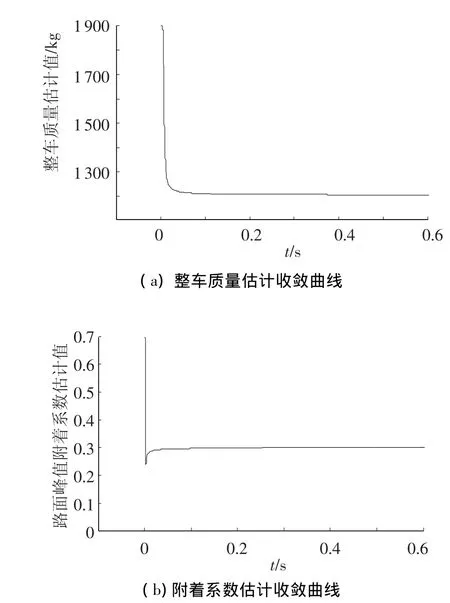
图4 低附着系数路面参数估计过程

3 基于行车参数估计的最高能量回收策略优化

最高制动能量回收控制策略是复合制动控制中常用的控制策略之一．最优能量回收控制策略的控制目标是最大程度的回收制动能量，因此，在分配前后轴机械制动力和再生制动力时，控制策略在保证要求的制动减速度和前后轮均不抱死的前提下尽量使再生制动力获得最大值，以尽最大可能回收制动能量．

在轻度制动下，采用纯再生制动，制动力完全由驱动电机提供;在中度和重度制动时，采用复合制动．具体的:复合初期，前轮液压制动力保持为零，优先增加后轮液压制动力，直到前后轮制动力分配落在理想制动力分配曲线I线上时，前后轮液压制动力一起上升，制动力分配比沿I线上升.

当系统估计出整车质量参数和地面附着系数后，新能源车辆进行复合制动过程控制时，便可以不局限于理想前后轮制动力分配线I线的约束，而把当前附着系数下后轮抱死线作为约束参数.即只要后轮不抱死，后轮液压制动力就可以继续增加，这样可以最大程度地降低液压制动在前轮上消耗能量.

对复合制动控制策略进行优化，具体的分配方法如下:

1)当再生制动系统的最大输出力矩Tmax大于整车制动所需的制动力Fbd时，制动力完全由驱动轮(前轮)电机再生制动提供，即再生制动力矩Tm=Fbd·r(r为车轮滚动半径)，前轮液压制动力Fhf和后轮液压制动力Fhr均为0.

2)当Tmax＜Fbd·r时，优先增加后轮液压制动力Fhr，Fhr的增加以对应整车载荷和地面附着系数下的后轮抱死线r线为约束，保证最终分配的结果在r线的下方，保证车辆后轮不会抱死，维持车辆制动方向稳定性.为了防止车轮抱死的风险，将Fhr控制在其最大值的90%.

对于3自由度整车模型，r线的方程为

且Tmax＜ Fbd·r时，再生制动力矩Tm=Tmax，后轮液压制动力Fhr=Fbd－Tmax/r，前轮液压制动力Fhf=0.

3)当Tmax≥Fbd·r，且后轮液压制动力分配在Tmax对应的r线下90% 的位置上时，总制动力仍然不能满足总制动力需求，此时前液压制动力上升，但是要保证制动力分配点不能落在I线的上方.此时

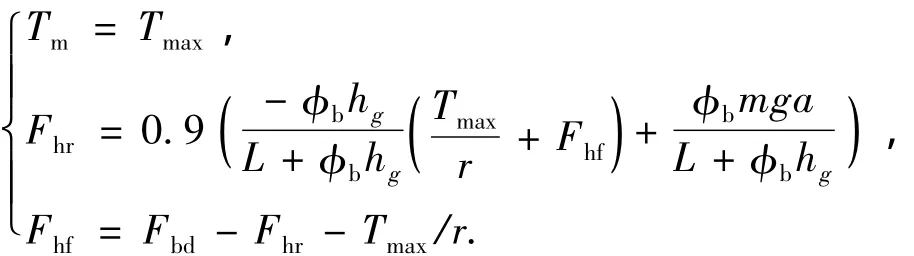
4 优化前后策略控制效果仿真分析

设定地面附着系数为0. 3，仿真优化前后复合制动系统的工作过程如图5～7所示．

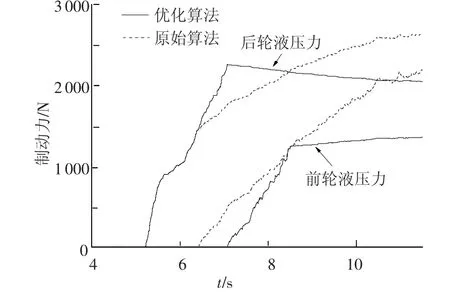
图5 优化前后再生制动控制算法制动力分配结果对比

从图5和6可以看出，优化后的算法中，前轮液压制动力的介入时间不再是原算法中的前后轮滑移率相同的时刻，而是当后轮滑移率达到15%以上时，前轮液压才开始介入．优化后的算法中，前轮液压制动力始终处于原始算法分配结果的下方，为再生制动提供了更大的空间．原始算法中由于没有针对路面附着状况进行制动力限制，在目标制动强度增大时，前后轮依次出现了抱死拖滑的情况．

图6 优化前后车轮滑移率控制结果对比

从图7可以看出，在原始算法控制下，前轮和后轮依次抱死．由于前轮的抱死，蓄电池充电电流迅速下降，无法再进行能量回收．在优化后的算法中，由于识别出了路面附着参数，避免了车轮抱死的状态，制动能量的回收可以一直维持．能量回收从75 kJ上升到90 kJ，总的回收效率提高了5.7%．

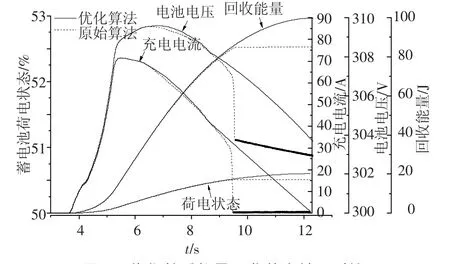
图7 优化前后能量回收状态结果对比

5 结论

1)结合新能源汽车复合制动系统的结构特点，建立并仿真验证了行车状态参数估计算法;

2)提出了基于行车状态参数估计的最高能量回收控制算法的优化方法;

3)利用建立的硬件在环仿真环境，仿真分析并对比了算法优化后的控制过程及控制效果．硬件在环仿真数据表明，优化后的算法有效提升了能量回收的效率并避免了车轮的抱死现象．

［1］NAKAMURA E，SOGA M．Development of electronically controlled brake system for hybrid vehicle［J］．SAE paper，2002－01－0300．

［2］SOGA M．Development of vehicle dynamics management system for hybrid vehicles:ECB system for improved environmental and vehicle dynamic performance［J］．SAE review， 2002，23:459－464．

［3］CAO Binggang．Research on control for regenerative braking of electric vehicle［C］//IEEE International Conference on Vehicular Electroics and Safety Proceedings．Xi＇an China:［s．n．］，2005:92 －97．

［4］LIN Chan-chiao．Power management strategy for a parallel hybrid electric truck［J］．IEEE Transactions on Control Systems Technology， 2003，11(6):839－850．

［5］舒红，秦大同．轻度混合动力汽车再生制动能量管理策略［J］．机械工程学报， 2009，45(1):167－173．

［6］YANG Jin．A model-based design analysis of hydraulic braking system［J］．SAE Paper，2003 －01 －0253．

［7］ZHANG Chuanwei，BAI Zhifeng．Study on regenerative braking of electric vehicle［C］//4th International Power Electronics and Motion control Conference．Xi＇an，China:［s．n．］，2004．836 －839．

［8］余卓平，左建令，陈慧．基于四轮轮边驱动电动车的路面附着系数估算方法［J］．汽车工程， 2007，29(2):141－146．

［9］刘清河，孙泽昌．新能源汽车电液复合制动系统研究［J］．高技术通讯，2010(5):251－258．

［10］LIU Qinghe，SUN Zechang．Research on electro － hydraulic parallel brake system for electric vehicle［C］//2006 IEEE International Conference on Vehicular Electronics and Safety Proceedings．Shanghai，China:［s．n．］，2006:376 －379．

［11］魏学哲，孙泽昌．锂离子动力电池参数辨识及状态估计［J］．同济大学学报:自然科学版， 2008，36(2):231－235．

States estimation control strategies for EV hybrid brake system

LIU Qing-he1，LIU Tao1，SUN Ze-chang2

(1．School of Automobile Engineering，Harbin Institute of Technology at Weihai，264209 Weihian，Shandong，China，qingheliu@sina．com;2．Automotive School，Tongji University，201804 Shanghai，China)

Based on the analysis of disadvantages of present static distribution control strategies of clean energy vehicles regenerative brake system，vehicle operation parameters estimation algorithm is presented which is adapted to the configuration of clean energy vehicles．The algorithm effect is simulated in Hardware-In-Loop-Simulation environment．Maximum energy regeneration optimization strategy is given and the advantages of control effect are simulated using HILS．The simulation data shows that the optimized strategy proves the efficiency of brake energy regeneration and finishes wheel anti-lock effectively．

clean energy vehicle;Hybrid Brake;road friction coefficient;states estimation

TP271

A

0367－6234(2011)09－0091－04

2010－04－14．

国家高技术研究发展计划资助项目:电动汽车重大专项(2003AA501033);上海市科技攻关计划(07dz12032);威海市科技发展计划资助项目(2010－3－96)．

刘清河(1977—)，男，博士，讲师;

孙泽昌(1953—)，男，教授，博士生导师．

(编辑 杨 波)