IR-UWB近距离实孔径成像系统分辨率

黄冬梅，张钦宇

(哈尔滨工业大学深圳研究生院，518055深圳，huangdongmei@126.com)

IR-UWB近距离实孔径成像系统分辨率

黄冬梅，张钦宇

(哈尔滨工业大学深圳研究生院，518055深圳，huangdongmei@126.com)

为了解决传统“窄带、远场”分辨率计算公式不再适用于超宽带极窄脉冲(IR－UWB)近距离实孔径成像系统的问题，提出了一种新的分辨率的计算方法.通过对IR－UWB近距离成像原理的分析，推导了单天线在距离向及横向分辨率的解析表达式，结合图像重建过程中信号叠加原理，提出了一种实孔径均匀线阵分辨率的计算方法.通过对理想点目标成像结果的数值仿真，验证了该分辨率计算方法的正确性.

分辨率;超宽带极窄脉冲;实孔径天线阵;近场;成像

近些年，超宽带极窄脉冲(Impulse Radio Ultra－Wide Band，IR－UWB)实孔径成像系统，如探底雷达、穿墙成像系统等备受关注［1－2］.其中分辨率的计算对成像系统设计、算法实施和实际成像过程非常重要.然而受到超宽带、近距离、实孔径的影响，系统工作于“窄带、远场”的假设条件不再成立，传统分辨率计算公式［3－4］不再适用.此外，在典型的近场IR－UWB实孔径成像系统中，为表示方便，通常采用类似于合成孔径雷达中的直角坐标系表示，认为天线阵轴线延伸的方向为横向，而与天线阵轴线垂直的方向为距离向，严格的讲这与传统的横向、距离向的定义有区别.并且目标不再始终位于孔径中心线方向，当目标不在天线阵中心线方向时，目标的图像会出现一定程度的偏斜，此时通过传统的角度分辨率来分析与天线阵孔径平行的横向分辨率亦不方便［5］.

文献［6－7］基于非相干三角定位技术分别对超宽带雷达系统的分辨率进行了定性和定量的分析，指出了“有限距离”下的距离分辨率是空间变化的，但是没有给出有限距离下的方位向分辨率表达式，并且没有考虑利用由多个阵元组成的天线阵进行探测成像时系统的分辨率.文献［8－10］从波束形成的角度分析了IR－UWB阵列的远场角分辨率，利用角分辨率分析方位分辨率，并给出了方位向分辨率的粗略计算公式.文献［11－12］推导了“大方位积累角”冲激SAR的方位向分辨率估计公式，但是仅给出了天线瞄准线方向的分辨率计算公式，且基于目标距离相对于天线阵孔径比较大的假设条件，公式并不能完全反映近场成像系统分辨率的空间变化特性.

目前对分辨率的研究多通过角分辨率来分析横向分辨率，并且没有充分考虑近场、实孔径条件的影响.因此，本文基于理想的系统、点目标模型［13］对IR－UWB近距离实孔径成像系统进行分析，提出了一种新的IR－UWB近场实孔径成像系统分辨率的计算方法，并利用数值仿真验证了该方法的正确性.对IR－UWB近距离成像系统的设计具有重要的指导意义.本文在讨论分辨率时，以图像中强度相同的2个目标点峰值之间的凹陷大于 －3 dB 的情况视为正确分辨［14－15］.

1 IR－UWB近距离实孔径成像系统分辨率计算

不考虑信号传播过程中的波形失真，假设探测环境为自由空间，天线为全向理想点天线，发射天线为单个天线，发射IR－UWB信号，接收天线为均匀线性阵列，阵列孔径为L，阵元间距为d，阵元数量为N，发射天线位于接收天线的中心位置.以发射天线为原点，接收天线阵为x轴建立直角坐标系，则发射天线的坐标为xT=( 0，0);接收天线阵中各阵元的坐标为 xi=(xi，0)，i= 1， 2，…，N/2.通常限定探测区域为y＞0的半区.常用的成像方法为后向投影(BP)算法［ 2，16］.假设在探测区域(xp，yp)处有1 个理想的点目标 δ(xp，yp)，经过BP成像处理后，由单个天线接收到该点目标回波恢复出的图像为具有一定宽度的一段椭圆，椭圆以发射天线和接收天线为焦点，接收信号的时间延迟对应的空间距离的一半为长轴.不同接收天线对应的“椭圆”相交于目标点的位置，在图像空间叠加后产生1个峰值，便形成了改点目标的图像.

1.1 单天线在x、y方向分辨率

设由天线xi=(xi，0)接收的点目标 xp=(xp，yp)的回波恢复的椭圆为eP，椭圆的焦点分别为发射天线xT和接收天线xi，长轴为

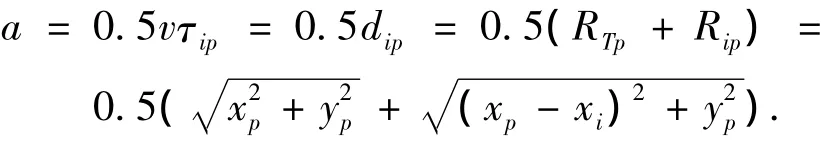
其中:τip为信号从发射天线传播到点目标，再后向传播到接收天线的双程回波时延;dip为对应的双程距离;RTp为点目标到发射天线的距离;Rip为点目标到接收天线的距离;v为电磁波在介质中的传播速度.

若单个阵元对空间2个目标可以分辨，则要求接收的2个目标的回波信号在时间上可分辨.假如发射的IR－UWB信号的时间分辨率为Δτ=Tw，对应的双程距离为Δdi=vTw.根据这个距离可以确定另外2个椭圆e1、e2，椭圆的焦点与eP相同，长轴距离分别为(dip－vTw)/ 2，(dip+vTw)/ 2，如图1所示.在椭圆e1、e2上的目标回波与目标xp的回波在时间上刚好可以分辨，这2个椭圆共同决定了系统在xp点(图1中P点)处各方向分辨率，称这2个椭圆围起的闭合区域(如图中的阴影区)为不可分辨区.以椭圆的中心(xi/ 2，0)可以建立1个新的直角坐标系x'O'y'，根据坐标变换定理有

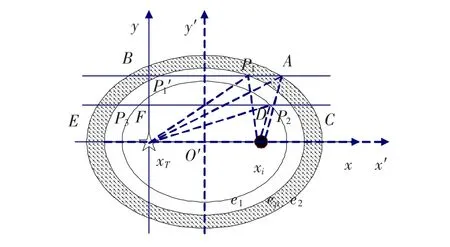
图1 x方向分辩率

首先考虑x方向的分辨率，由于分辨率在正、负方向不一定相同，因此需分别考虑.过目标点做一与x轴平行的直线，如图1所示，直线与椭圆e1，e2的交点即决定了目标点处x方向的分辨率.从图1中可以看出，直线与椭圆e2一定存在2个交点，但是与椭圆e1可能相交，也可能不相交.根据直线与椭圆e1是否相交，将x方向分辨率的计算分为两种情况:

1)直线与椭圆e1没有交点，如点P1.此时，椭圆e1对x方向分辨率没有贡献.过目标点的直线与大椭圆e2相交于两点A、B，这两点分别决定了目标点处沿 +x及 －x方向的分辨率.

2)直线与椭圆e1有交点，如点P2.此时，直线有两部分处在椭圆e1、e2确定的阴影区域中，利用天线阵中多个阵元的协作，可以很容易的去除与目标点相距较远的直线段的影响，因此只考虑目标点所在的那部分直线段.直线分别与椭圆e2、e1相交于点C、D，这两点分别确定了目标点沿 +x及 －x方向的分辨率.

当目标点的纵坐标yp＞b1时，属于第一种情况.直线与椭圆e2相交于点A、B.将P的纵坐标代入式(1)，并令m= 2，消掉参考角度θ可以求得2点的横坐标分别为其中x'p=xp－xi/2为目标点在新坐标系中的横坐标.－x方向的分辨率为

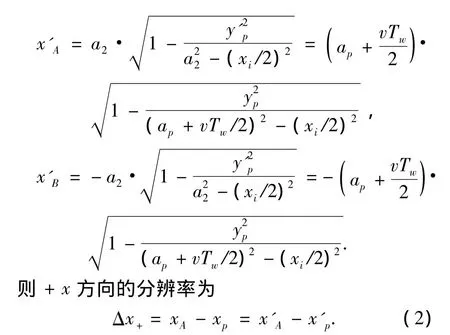
当yp≤b1时，属于第二种情况.此时，直线段与椭圆e1、e2分别相交于两点D、C或E、F，这与目标点的位置有关.当xp≥xi/2时，目标点位于图1中P2位置，离目标点较近的两个交点为C、D.将P的纵坐标代入式(1)，分别令m= 1， 2，消掉参考角度θ可得2点的横坐标分别为

当xp＜xi/2时，目标点位于图1中P3位置，离目标点较近的两个交点为E、F，它们的横坐标分别为

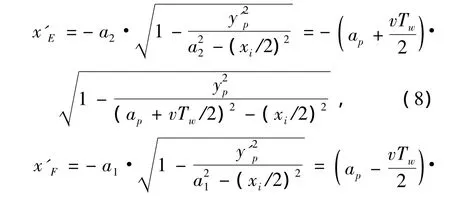
从式(2)～(11)可以看出，单个阵元的x方向分辨率分为 +x、－x方向，两个方向的分辨率不一定相等，它们不仅与IR－UWB信号的时间分辨率Tw、传播速度v有关，而且与目标位置xp和接收天线位置xi有关.

与x方向分辨率计算类似，过目标点做一与y轴平行的直线，根据直线与椭圆的交点可以确定单个阵元y方向分辨率.但需要注意成像系统中只对天线阵一侧y＞0的探测区域感兴趣，因此只考虑y＞0的半个椭圆与x轴形成的闭合区域，如图2所示.根据直线与椭圆e1是否相交，y方向分辨率的计算同样分为两种情况.当目标点的横坐标xp＞xi/2+a1或xp＜xi/2－a1时，直线与椭圆e1没有交点，为第一种情况.当目标点的横坐标xi/2－a1≤xp≤xi/2+a1时，直线与椭圆e1有交点，为第二种情况.具体的计算过程与x方向分辨率计算方法相同.y方向的分辨率同样分为+y及－y方向，两个方向的分辨率不一定相等，它们与IR－UWB信号的时间分辨率Tw、传播速度v、目标位置xp和接收天线位置xi有关.

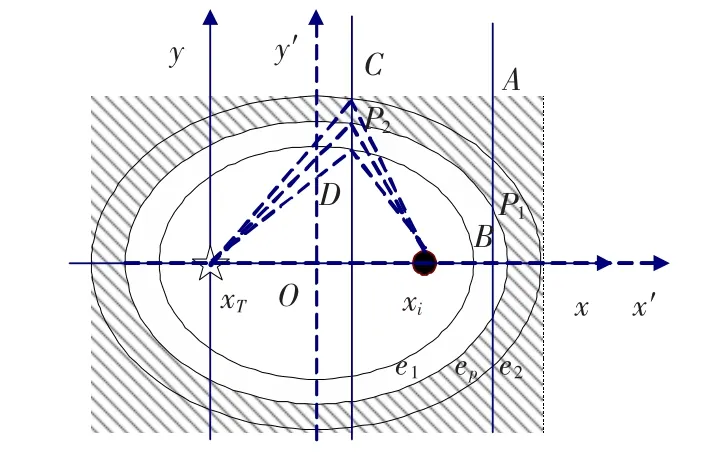
图2 y方向分辩率

1.2 实孔径均匀线阵近场分辨率

在成像系统中，为了获得一定的信噪比，天线阵通常由多个阵元组成.由上述的分析可知，不同位置的阵元对同一目标的分辨率不同，因此，如何确定整个实孔径天线阵实现的分辨率成为了一个难题.本节提出了一种新的分辨率计算方法.

受超宽带波束形成中波束主瓣－3 dB宽度计算方法［8－9］的启发，假设发射的 IR－UWB 信号为具有一定时间宽度的理想矩形脉冲，幅度为单位 1，不考虑幅度衰减，成像区域中有2个强度相同的点目标，由N个阵元组成的接收天线中各阵元接收到2个目标的回波信号，经过BP成像处理后分别在2个目标点的位置处叠加产生峰值，峰值幅度为N，而对于2个目标中间的区域，称之为凹陷区域，当天线阵中阵元对2个目标可以分辨率时，该阵元接收的回波信号对凹陷没有贡献，而当阵元对2个目标不可分辨时，该天线接收的2个目标的回波信号对凹陷都有贡献，即对凹陷处的贡献的信号幅度为2.当有Nnr个阵元对两目标无法分辨时，叠加后的图像凹陷处的信号幅度为2Nnr.如果此时凹陷处能量刚为目标峰值能量的－3 dB，则两个目标“刚好”可以分辨.实际上，在天线阵近场区域，单个阵元分辨率的变化范围比较大，例如当天线阵孔径长度为2 m时，xi=1的阵元对( 0，2)的 +x方向分辨率大约为xi=－1的阵元的3倍，此时若两目标的距离刚好为xi=－1的阵元的可分辨距离，则xi=1的阵元接收的信号不仅对凹陷处有贡献，还会对另一目标点处的信号产生影响，因此实际目标点峰值幅度将为N+Nnr.根据分辨率定义可得当2个目标刚好可以分辨时，Nnr与N的关系为

由于阵元数为整数，并且当2个目标可以分辨率时要求凹陷处的能量小于等于－3 dB，因此取

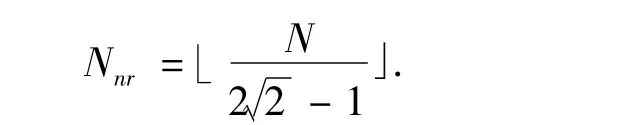
其中⎿·」表示向下取整.此时对两目标可分辨的阵元数为Nr=N－Nnr.由此可见，当天线阵对2个目标可以分辨时，并不要求所有的阵元对2个目标都可以分辨，它允许一部分阵元(Nnr个)对2个目标无法分辨.组成天线阵的阵元数越多，允许对目标不可分辨的阵元数越多.

根据上述分析，可以得到实孔径均匀线阵分辨率的计算方法为:

1)针对某个空间位置，计算天线阵中所有单个阵元在该点处的各方向分辨率;

2)对所有单个阵元在不同方向分辨率分别进行降序排列，选取第

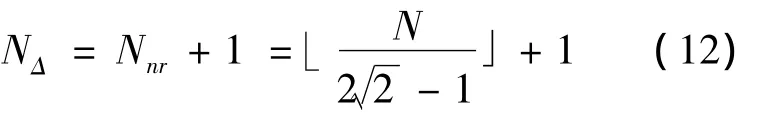
个最大的分辨率值，该值即为天线阵在该点处对应方向上可实现的分辨率.

对于不同的阵元数N，根据式(12)计算的NΔ以及可分辨阵元数Nr如表1所示.从表1可以看出，当有N=3个阵元时，只要有2个阵元对目标可分辨，则天线阵对2个目标即可分辨，这与文献［7］中的对角度分辨率的分析结果是一致的，并不需要所有的阵元对目标均可分辨.

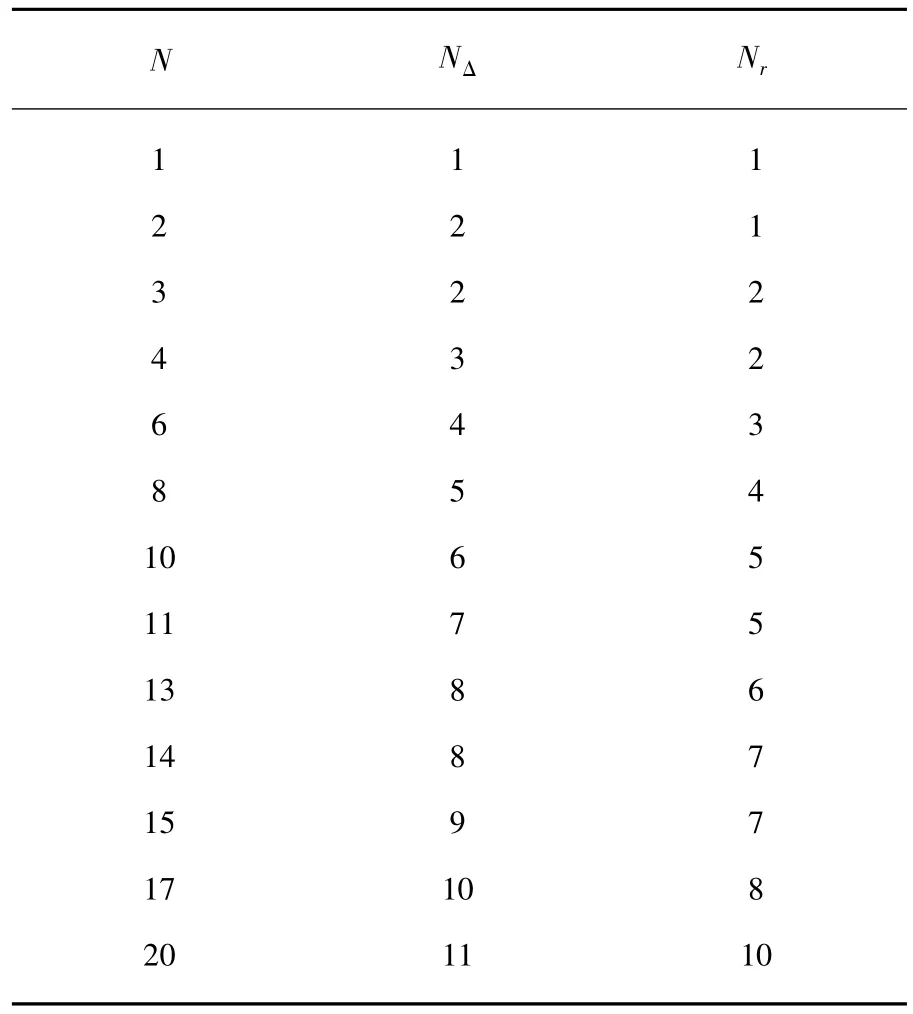
表1 阵元数N、NΔ及可分辨阵元数Nr

由于单个阵元在x或y正、负方向的分辨率不一定相同，由此得到的天线阵在正、负方向的分辨率也不一定相同，空间中的2个点在x或y方向是否可以分辨，需要比较两点之间的距离与两点在相互方向的分辨率.此时两目标是否可分辨的评定准则为:如果两目标点之间的距离大于相互方向分辨率的最大值，则两点在图像中可以分开;否则，一般情况下两点之间不可分.即:假设空间中有2 个点目标 P(xp，yp)、Q(xq，yq)，假设 yp=yq，xp＜xq，则两点在相互方向的分辨率分别为Δpx+、Δqx－，若xq－ xp≥max(Δpx+，Δqx－)，则两点可以分辨;否则认为两点不可分辨.为了方便与传统的分辨率相比，可以定义系统在空间各点的距离向(y方向)及横向(x方向)的分辨率分别为

2 仿真及结果验证

2.1 分辨率的空间分布

假设接收天线为沿x轴均匀分布的线性天线阵，孔径L=2 m，阵元数N=14.发射IR－UWB信号的时域分辨率为Tw=1 ns，自由空间下信号的传播速度为v=c=3×108m/s.利用本文所提出的方法计算［－ 3，3］×［ 0，3］空间内各点分辨率如图3所示，部分空间点的分辨率如表2所示.

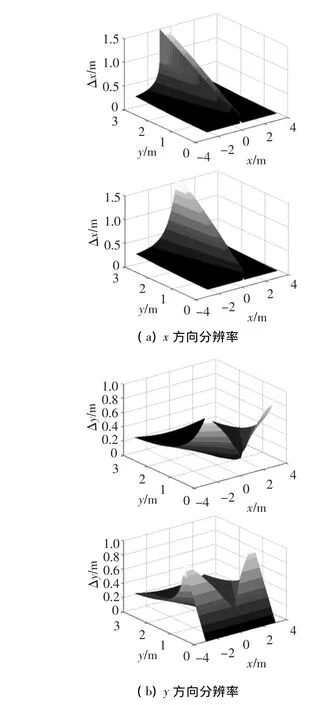
图3 天线阵各方向分辩率的空间分布

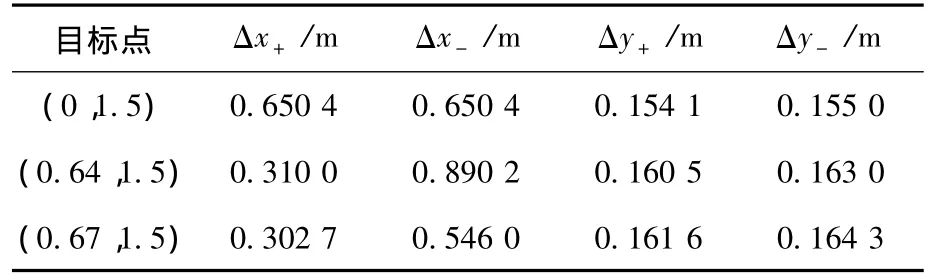
表2 部分点的分辨率

从图3中可以看出，受近场条件的影响，距离向(y方向)分辨率在天线阵的近场区域中不再恒定，而是空间变化的，传统的距离向分辨率计算公式在近场区域中不再适用.在天线阵附近，y方向的分辨率比较差，随着目标到天线阵的垂直距离yp的增加，距离向的分辨率逐渐减小，并趋近于经典的远场距离向分辨率cTw/2=0.15 m.而Δy－在天线阵附近比较小，是由于系统的成像区域限制在y＞0的区域而引起的(此时y方向分辨率的计算对应第一种情况).此外，由于对称的天线阵对中心线两侧的作用相同，y方向的分辨率以x=0的直线(天线阵的中心线)镜像对称.随着空间点逐渐偏离天线阵中心线，y方向的分辨距离逐渐增加.此时y方向的分辨率能力减弱，这是由于利用实孔径天线阵对偏离天线阵中心线方向的目标进行成像时出现偏斜而引起的.

横向(x方向)分辨率的空间变化相对比较复杂.受实孔径及近场条件的影响，Δx+、Δx－在天线阵附近区域比较小，趋近于cTw/2=0.15 m，随着yp的增加而逐渐增加.此外，由于天线阵是对称的，Δx+与Δx－的空间分布之间关于天线阵的中心线对称，Δx+、Δx－在中心线附近区域比较大，而在偏离中心线比较远的区域，天线阵的横向分辨率比较小，并且随着目标的逐渐偏离，x方向的分辨率逐渐变小，并趋向cTw/2=0.15 m.其中Δx+在中心线的左侧区域比较大，随着x的减小先增加，当x减小到一定值时，由于用于确定分辨率的椭圆(e1、e2)发生了变化，Δx+突然减小到一个比较小的值，并随着x的减小而逐渐减小;而在中心线右侧区域，Δx+随着x的增加而逐渐减小.

根据式(13)计算的空间各点横向及距离向分辨率如图4所示.从图4中可以看出，横向分辨率与距离向分辨率的空间变化趋势近似相反，因此在实际的系统设计过程中，对系统参数的选择需要考虑横向分辨率与距离向分辨率之间的折衷.

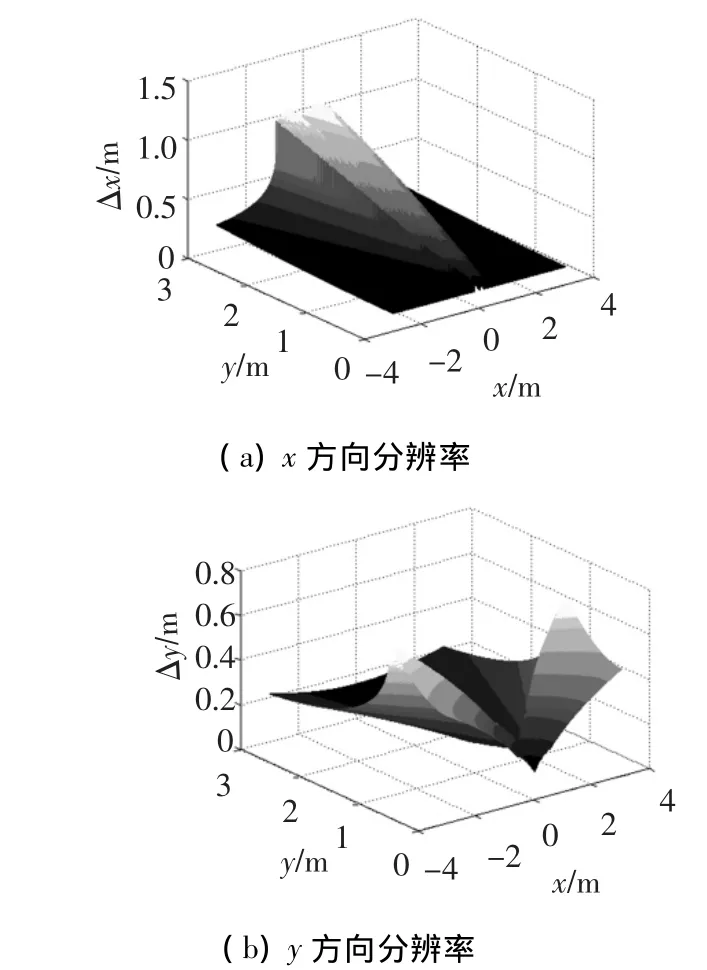
图4 距离向及横向分辩率

2.2 分辨率结果验证

根据1.2节中两目标是否可分辨的评定准则，比较表2中所列的空间点之间的距离及相互方向的分辨率，可以发现，( 0，1.5)、(0. 64，1.5)两点之间的距离小于相互分辨率的最大值，因此在图像中应该无法分辨.而( 0，1.5)、(0. 67，1.5)两点之间的距离大于相互分辨率的最大值，因此两点目标在图像中应该可以分辨.本节将利用数值仿真对本文所提出的分辨率计算方法进行验证.

假设发射IR－UWB信号为理想的矩形脉冲，脉冲持续时间(即时间分辨率)Tw=1 ns.利用图3中对应的天线阵对自由空间中位于( 0，1.5)、(0. 64，1.5)的 2个点目标进行探测成像，以－3 dB阈值对图像进行分割得到的二值图像及y=1.5 m时图像的剖面图如图5(a)所示.同样对 ( 0，1.5)、(0. 67，1.5)两个点目标的成像结果如图5(b)所示.从图5中可以看出，虽然( 0，1.5)、(0. 64，1.5)两点之间凹陷处信号小于峰值的－3 dB，但由于幅值小于－3 dB的距离很短，在二值图像中两点的图像连接到一起，无法区分;而( 0，1.5)、(0. 67，1.5)两点之间凹陷明显小于峰值的－3 dB，在二值图像中彼此完全可以分辨.与表2的分析结果完全一致，因此本文提出的分辨率的计算方法是有效的.

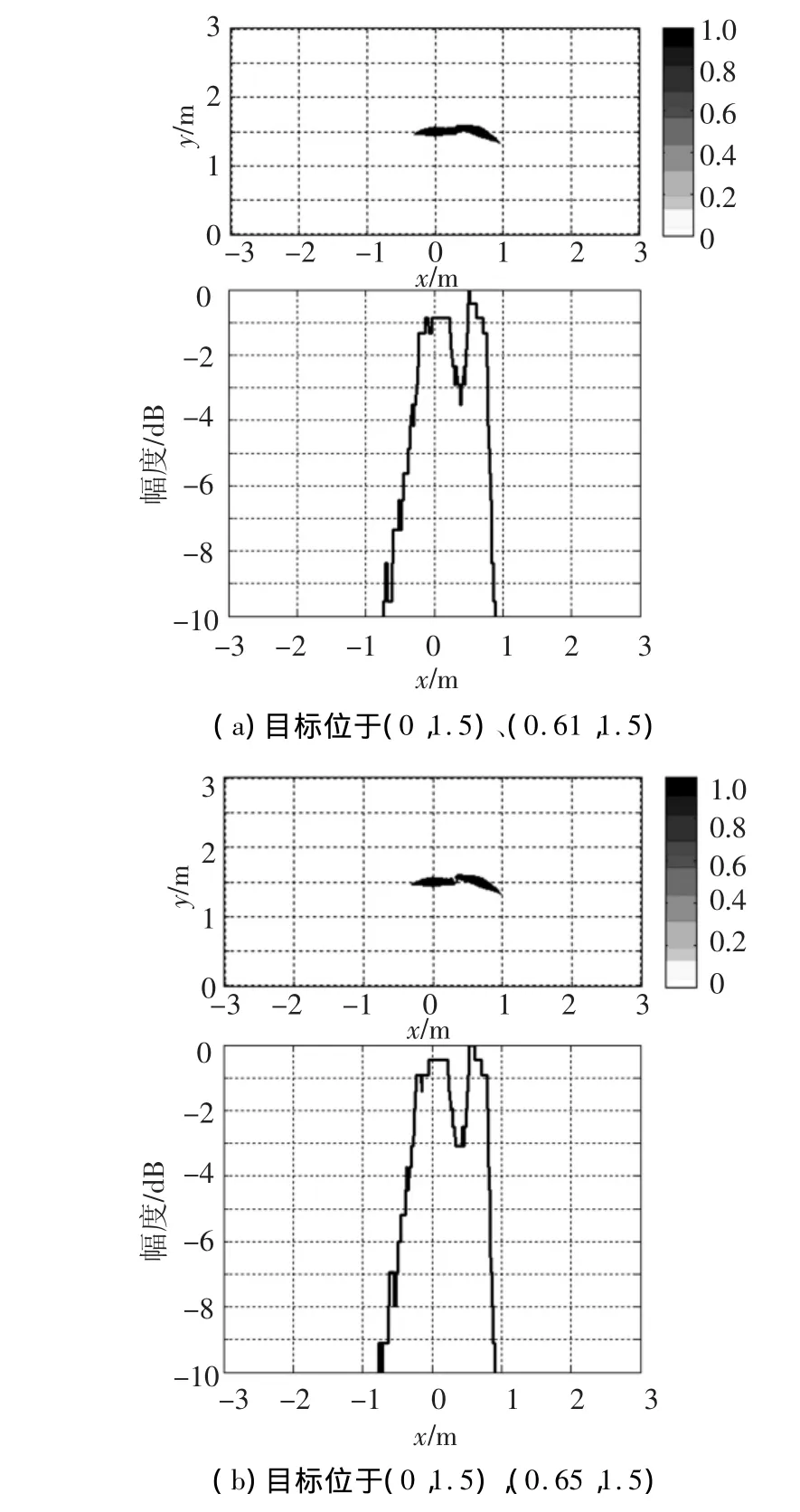
图5 发射矩形脉冲时的成像结果

实际中，通常发射的IR－UWB脉冲为高斯脉冲或高斯脉冲的导数.文献［15］指出对2个相同强度的理想信号来说，要区分它们并能精确测量它们的位置，两个信号的间距必须大于等于－3 dB宽度的 2倍.因此取 Tw=2T－3dB，其中T－3dB为信号 －3 dB时间宽度.假设发射的 IRUWB信号为归一化的高斯脉冲，即

脉冲的时间分辨率为Tw=2T－3dB=1 ns，对应的脉冲形成因子为α=1.066 3 ns，成像系统的其它参数不变，则对( 0，1.5)、(0. 64，1.5)两个点目标以及( 0，1.5)、(0. 67，1.5)两个点目标成像的结果如图6所示.从图中可以看出，两种情况下的目标均可以清晰分辨，原本不可分辨的( 0，1.5)、(0. 64，1.5)两点目标也可以很好的分辨.

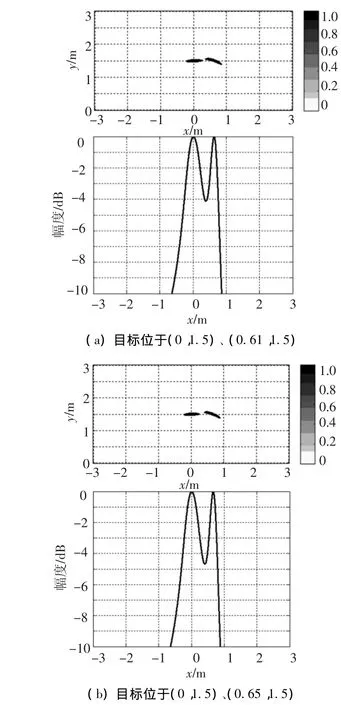
图6 发射高斯脉冲时的成像结果

对比图5、6可以看出，对于实际发射的IRUWB信号，系统的分辨率优于矩形脉冲时的系统分辨率，这与文献［9］中的结论一致.实际上，当发射脉冲时间分辨率相同时，本文提出的方法计算的分辨率对应着最差的分辨率，对于实际发射的信号波形，系统的分辨率会有不同程度的改善.但由于信号波形对分辨率的影响是全局性的，分辨率的空间总体变化趋势保持不变，因此本文提出的分辨率计算方法对系统的设计具有重要的指导意义.

3 结论

IR－UWB近距离实孔径成像系统中，窄带、远场的分辨率计算公式已经不再适用.本文基于理想的系统、点目标模型及BP成像算法的条件，通过对IR－UWB近距离成像原理的分析，推导了单天线的距离向、横向分辨率的解析表达式，结合图像重建过程中信号叠加原理，提出了利用实孔径均匀线阵探测成像时，系统分辨率一种计算方法.并利用数值仿真验证了该分辨率计算方法的正确性.

1)本文所提出的方法计算的分辨率对应着系统最差的分辨率，对于实际发射的信号波形，系统的分辨率会有不同程度的改善，但总体变化趋势不变.相对于窄带、远场条件，受超宽带、近场及实孔径的影响，距离向分辨率不再恒定，距离向及横向分辨率的空间变化更加复杂，横向分辨率与距离向分辨率的空间变化趋势近似相反，因此在实际的系统设计中，需要考虑横向与距离向分辨率之间的折衷.

2)本文提出的分辨率计算方法，不但适用于对点目标的成像，而且适用于对复杂目标的成像［13］.利用本文的思想还可以计算近距离非相干成像、定位系统的空间分辨率.对IR－UWB近距离成像系统的设计具有重要指导意义.下一步工作将进一步分析分辨率与系统参数的关系.

［1］YAROVOY A G，SAVELYEV T G，AUBRY P J，et al.UWB array－based sensor for near－field imaging［J］.IEEE Trans on Microwave Theory and Techniques， 2007，55(6):1288－1295.

［2］ CHEN Lei，SHAN Ouyang.Through－wall surveillance using ultra－wideband short pulse radar:numerical simulation ［C］//Industrial Electronics and Applications，2007.ICIEA 2007.Piscataway:IEEE，2007:1551－1554.

［3］JOHN P F.Synthetic aperture radar［M］.New York:Spirnger－Verlag，1988.

［4］ MERRILL S.Radar handbook［M］.New York:McGraw－Hill Publishing Co，1990.

［5］杨延光，周智敏，宋千.分裂孔径发射阵列接收BP算法方位分辨率分析［J］.信号处理， 2008，24(5):752－756.

［6］陈洁，方广有，李芳.超宽带穿墙雷达非相干成像方法［J］.中国科学院研究生院学报， 2007，24(6):829－834.

［7］ AHMAD F，AMIN M G.Noncoherent approach to through－the－wall radar localization ［J］.IEEE transactions on Aerospace and Electronic Systems， 2006，42(4):1405－1419.

［8］HUSSAIN M G M.Principles of Space－time array processing for ultrawide－band impulse radar and radio communications［J］.IEEE Transaction on Vehicular Technology， 2002，51(3):393－403.

［9］RIES S，KAISER T.Ultra wideband impulse beamforming:it is a different world ［J］.Signal Processing， 2006，86:2198－2207.

［10］KAISER T，ZHENG F，DIMITROV E.An overview of ultra－wide－band－systems with MIMO ［J］.Proceedings of the IEEE， 2009，97(2):285－311.

［11］粟毅.冲激脉冲SAR成像理论与方法研究［D］.长沙:国防科技大学，2001.

［12］吕彤光，陆仲良，粟毅，等.冲激信号SAR成像的方位分辨率分析［J］.电子学报， 2000，28(6):40－43.

［13］匡纲要.UWB雷达目标建模和信号设计［D］.长沙:国防科技大学，1996.

［14］盛卫星.微波成像技术及应用［D］.南京:南京理工大学，2001.

［15］WEHNER D R.High－resolution radar［M］.Norwood，MA:Artech House，1994.

［16］DESAI M D，JENKINS K.Convolution backprojection image reconstruction for spotlight mode synthetic aperture radar ［J］.IEEE Trans on Image Processing， 1992，1(4):505－517.

Resolution of IR-UWB near-field real-aperture imaging systems

HUANG Dong－mei，ZHANG Qin－yu

(Shenzhen Graduate School，Harbin Institute of Technology，518055 Shenzhen，China，huangdongmei@126.com)

To solve the problem that the traditional“narrow－band，far－field”resolution formulas are no longer suitable for Impulse Radio Ultra－Wide Band(IR－UWB)real aperture imaging systems，a new algorithm to compute the resolution was proposed.On analysis of IR－UWB near－field imaging principle，the formulation of resolution in down－and cross－range for single antenna was derived.Combined with signal superposition in the process of imaging，an algorithm to compute the resolution for real－aperture uniform linear array was presented.Numerical simulation results of ideal point targets imaging verified the correctness of the algorithm.

resolution;IR－UWB;real－aperture antenna arrays;near－field;imaging

TN985

A

0367－6234(2011)09－0067－07

2010－04－05.

国家自然科学基金资助项目(60702034).

黄冬梅(1982—)，女，博士研究生;

张钦宇(1972—)，男，教授，博士生导师.

(编辑 张 宏)