新型煤矿救援机器人的特殊运动逆运动学

刘 罡，刘玉斌，赵 杰，朱 磊

(哈尔滨工业大学机器人技术及系统国家重点实验室，150001哈尔滨，liuxing338@163．com)

新型煤矿救援机器人的特殊运动逆运动学

刘 罡，刘玉斌，赵 杰，朱 磊

(哈尔滨工业大学机器人技术及系统国家重点实验室，150001哈尔滨，liuxing338@163．com)

针对新型煤矿救援机器人头部单元的特殊运动(位姿调整)，提出了一种基于空间分割和遗传算法相结合的新方法求解其逆运动学．该方法能以最小的转动代价实现期望的位姿，有利于保持机器人稳定．采用二次空间分割法，解决了遗传算法搜索空间大，难以收敛到全局最优解的问题．仿真实验结果表明，采用新的逆运动学算法得出的位姿误差较小，而且关节角更加接近真实值，满足新型煤矿救援机器人头部单元的运动要求．

救援机器人;逆运动学;空间分割;遗传算法

煤矿救援机器人主要用来进行井下事故现场的探测，辅助救援人员顺利完成救援任务．哈尔滨工业大学机器人技术及系统国家重点实验室研制了一款新型煤矿救援机器人，该机器人由4个单元串联而成，相邻单元之间具有2个自由度，可以实现俯仰和偏航运动，运动范围为±45°．机器人头部单元安装有摄像头、照明灯、超声传感器和各种气体传感器，可以探测机器人周围的环境信息，并将信息传回控制中心．新型煤矿救援机器人是一种典型的无根开链式结构，与具有固定基座的串联机器人(如PUMA机器人等)相比，在调整头部单元位姿的特殊运动中很容易发生倾覆现象，即头部单元和尾部单元都翘起;因此，其逆运动学研究关键是如何找到既能满足头部单元位姿精度要求，又能有利于保持机器人稳定的逆解．

目前，关于机器人逆运动学求解的方法很多，主要有解析法和数值法［1－3］．解析法虽然具有求解速度快、效率高、便于实时控制的优点，但是机器人结构必须满足一定的几何条件才能求得解析解．数值法包括直接法和间接法．直接法主要是通过求解雅可比矩阵求出机器人各关节速度变量．对于冗余机器人来说，雅可比矩阵不是方阵，需要对雅可比矩阵进行扩展［4－6］．在机器人末端到达期望位姿的过程中，直接法存在奇异问题．常见的间接法有信赖域法［7－8］、CCD 法［9］、遗传算法［10－11］、神经网络算法［12－13］等．由于所研究机器人的关节空间和位姿空间存在复杂的非线性映射关系，无法通过解析法获得关节角度的解析解．遗传算法作为一种非确定性的拟自然算法，具有很好的鲁棒性、自适应性、全局优化性和隐含并行性，可以实现关节空间和位姿空间的非线性映射．但是，遗传算法很难保证收敛到全局最优解［14］．

本文针对新型煤矿救援机器人的特殊结构，提出了一种基于空间分割和遗传算法相结合的新算法，求解机器人调整头部单元姿态的特殊运动逆运动学．

1 机器人模型

针对头部单元的位姿调整运动，新型煤矿救援机器人有6个自由度(3个俯仰关节和3个偏航关节)，以机器人尾部单元为固定基座，其模型示意图如图1所示．机器人D－H参数如表1所示．

图1 新型煤矿救援机器人模型

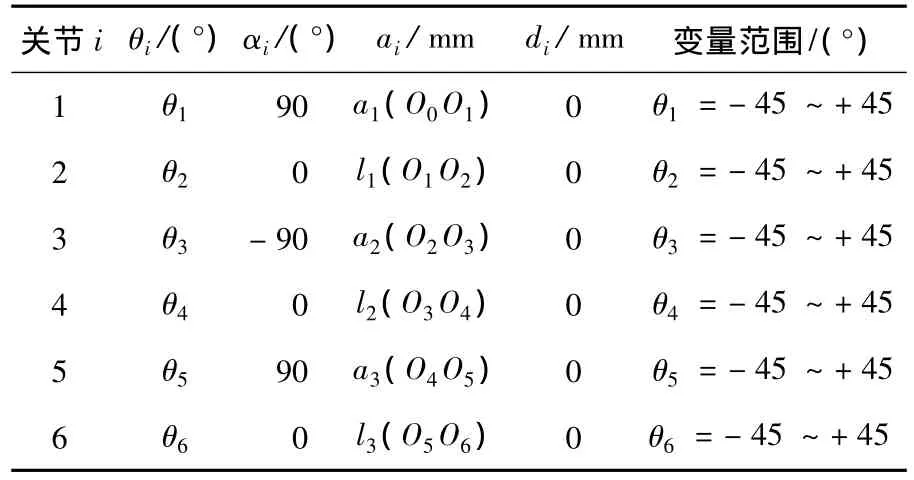
表1 头部单元姿态调整D－H参数

机器人头部单元在其基坐标系中的位姿可描述为

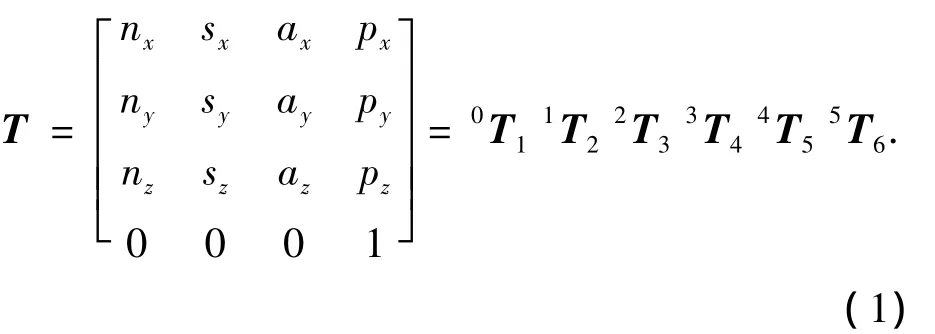
其中，i－1Ti表示坐标系i－1到i的齐次变换矩阵．将相邻坐标系间的坐标变换矩阵代入式(1)，得到如式(2)所示的头部单元位置表达式:

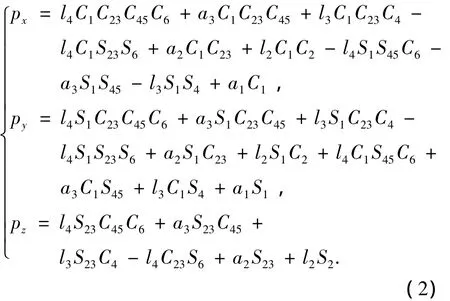
其中，Si表示 sin θi，Ci表示 cos θi，Sij表示 sin(θi+θj)，Cij表示 cos(θi+ θj)．

2 空间分割

新型煤矿救援机器人运动学逆解除了要满足一定的精度要求之外，还要有利于保持机器人稳定，这一点是至关重要的．假如转动关节角θ6就能到达期望的位姿，其他关节角就不需转动．然而，由图1可知，基于遗传算法的逆运动学求解算法，其搜索空间为R6．所以无论机器人头部单元的位姿如何，算法都要在R6空间内搜索逆运动学的最优解．由于遗传算法无法保证收敛到全局最优解，结果很可能是每个关节角都需转动，这对于保持机器人稳定是不利的．如何灵活地配置算法的搜索空间是解决新型煤矿救援机器人逆运动学求解的关键．

文献［14－15］根据正运动学计算出机器人末端可达的位姿空间，然后根据一定原则将所得到的位姿空间划分为若干个大小相同的超立方体，并依次进行编码，然后根据期望位姿确定其所在的子空间，并在该子空间内寻找最优解．事实上，上述空间分割方法只对工作空间进行了分割，而没有对关节空间进行分割，所得到的子空间是彼此不相交的，不存在包含关系．如果将上述空间分割方法应用于新型煤矿救援机器人逆运动学的求解，无法解决算法搜索空间的灵活配置问题．

本文提出一种新的空间分割方法，如图2所示．该方法的核心思想如下:首先将机器人的关节空间进行分割，形成若干个子关节空间;然后，利用正运动学求解每个子关节空间对应的子工作空间;最后，确定期望位姿所在的子工作空间，再反推得到对应的子关节空间，将此子关节空间作为遗传算法的搜索空间，从而实现根据不同的期望位姿来配置不同的搜索空间．

图2 空间分割流程

空间分割的具体方法可描述如下:

Step1 将转动关节空间进行一次分割，形成6个子关节空间．即当只有θ6关节转动而其他关节不动时，对应的子关节空间为S1，对应的子工作空间为W1;当只有θ5和θ6关节转动而其它关节不动时对应的子关节空间为S2，对应的子工作空间为W2;依此类推可以得到6个子关节空间和6个子工作空间．

Step2 将每个子关节空间进行二次分割．首先，机器人的每个关节转角划分为0～45°和－45°～0两个子区间，然后在每个子关节空间内对关节转角区间进行排列组合形成2i个次子关节空间Sij，其中i为子关节空间的序号，j为第i个子关节空间中的次子关节空间序号．然后，根据机器人正运动学计算各次子关节空间对应的次子工作空间．分割后的机器人各关节空间和对应的工作空间如表2所示，整个关节空间被分割成126个次子关节空间．

按照上述空间分割方法，6个子关节空间和6个子工作空间彼此存在包含关系，其包含关系如下所示:

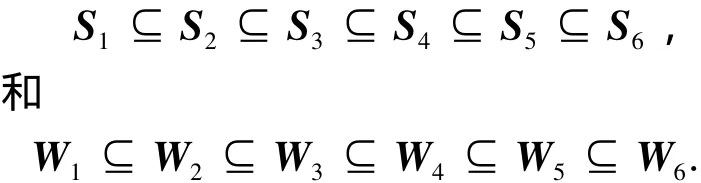
工作空间的序号越小，其被作为搜索空间的优先级就越高．另外，在每个子关节空间内，次子关节空间彼此不存在包含关系，而在每个子工作空间内，次子工作空间彼此可能存在相交关系．因此，期望位姿可能同时隶属于不同的次子工作空间．

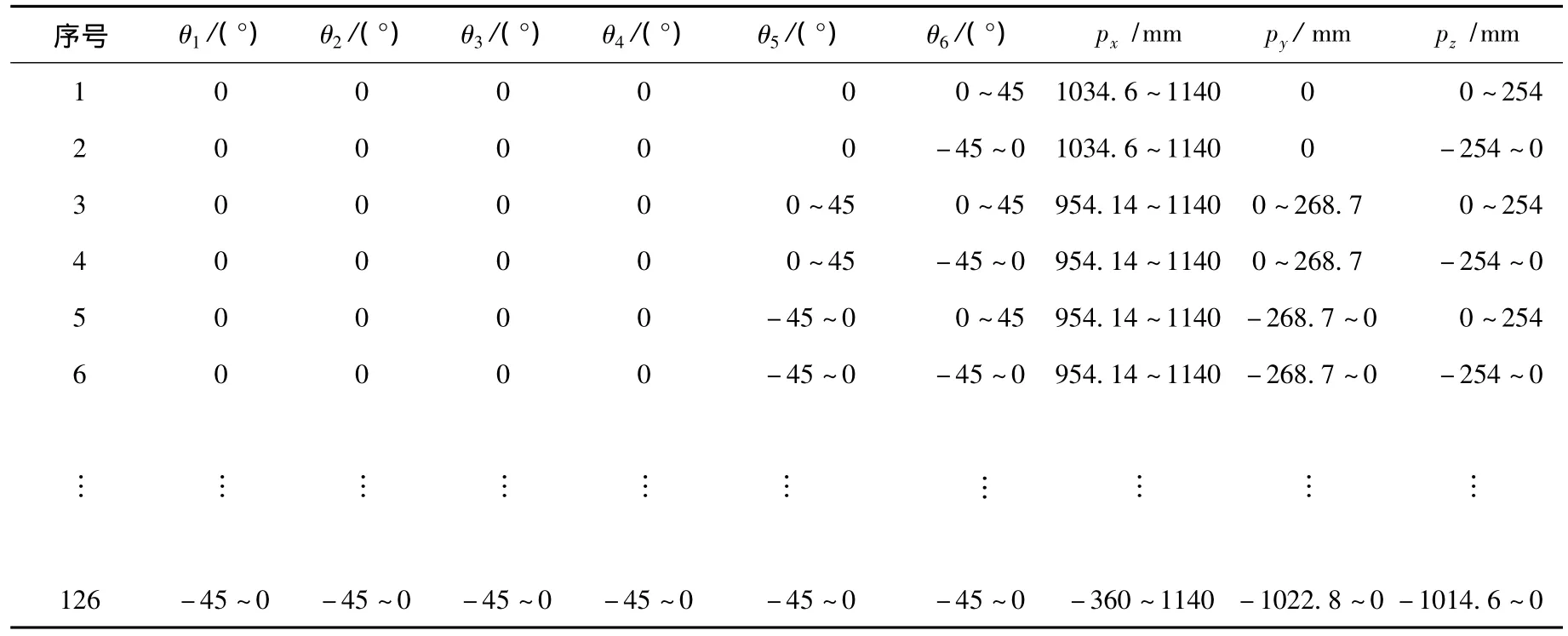
表2 各次子关节空间及对应的次子工作空间

3 基于遗传算法的逆运动学

由于在子工作空间Wi中，次子工作空间存在交叠的情况，因此首先确定期望位姿所在的子工作空间，然后再确定期望位姿所属的全部次子工作空间，通过反推查表确定其对应的次子关节空间Sij，最后将Sij作为遗传算法的搜索空间求取运动学的逆解．

基于遗传算法求逆运动学的流程如图3所示．

基于遗传算法的逆运动学解法可描述如下:

Step1 初始化参数．

Step2 对机器人工作空间进行一次分割，产生6个子工作空间，然后确定期望位姿所属的子工作空间Wi，再反推得到其对应的子关节空间Si．

Step3 对Wi进行二次分割，产生2i个次子工作空间，然后确定期望位姿所属的全部次子工作空间，再反推得到其对应的次子关节空间SubS，令j=1．

Step4 根据确定的次子关节空间SubS(j)和求解精度，设置染色体长度，进行二进制编码．

Step5 初始化种群．种群的大小一般取为50～ 500，这里取100．

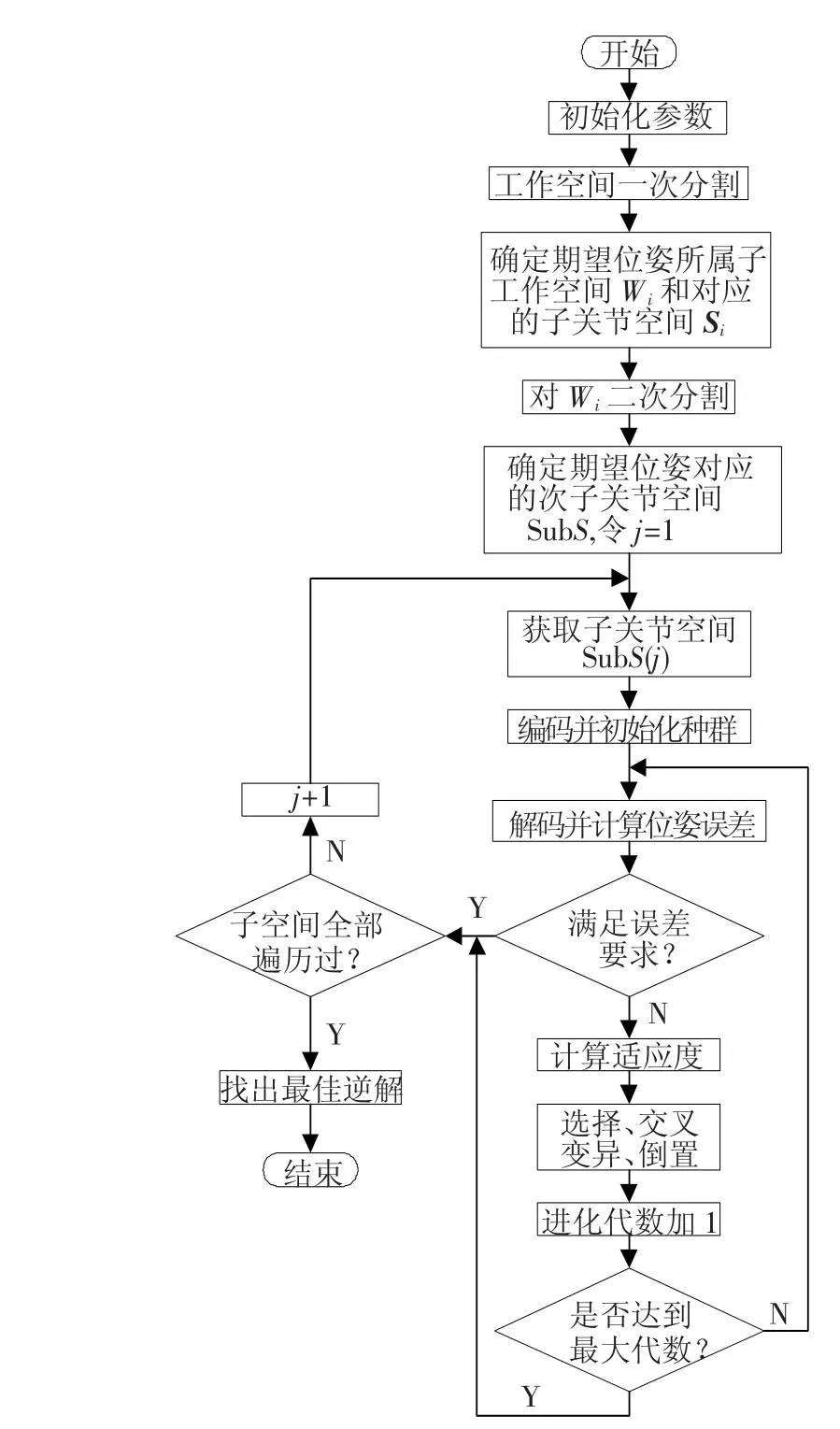
图3 机器人逆运动学算法流程图

Step 6 解码．将二进制编码通过解码转换成十进制的关节角，根据新产生的关节角计算位姿误差，若误差满足精度要求，转向Step 11，否则转向Step7．

Step 7 计算适应度．运动学逆问题可以转化为一般数值优化问题，问题描述为:已知目标位置向量Pi，在机器人的关节活动范围内搜索一组关节变量组成解向量 Q =［θ1θ2θ3θ4θ5θ6］T，使得机器人的手部位姿与离散点的位姿差异ΔE最小，则当两者重合时的解向量Q=［θ1θ2θ3θ4θ5θ6］T为问题的最优解．因此，优化目标函数定义如下:

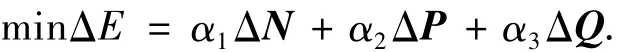
其中，ΔN为机器人头部单元姿态与目标点姿态之差;ΔP为机器人头部单元位置与目标点位置之差;ΔQ 为各关节转角绝对之和;α1、α2和 α3为权因子，可以分别对姿态因子、距离因子和转角之和因子的重要程度进行加权．根据优化目标函数定义适应度函数如下:

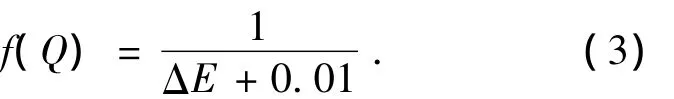
式中:0.01是为了避免出现零分母．根据式(3)计算各个个体的适应度值．

Step8 遗传操作．采用非线性排名选择和锦标赛选择，均匀交叉和多点交叉，随机变异．

Step9 倒置．为了避免算法早熟，增加了倒置操作．根据倒置概率的大小筛选出需要倒置的个体，随机生成倒置的起始和终止位置，然后将起始和终止位置之间的基因颠倒．

Step10 进化代数加 1，若超过最大代数，转向Step 11，否则转向Step6．

Step11 若子关节空间SubS都遍历过，找出最佳的逆解，程序结束;否则j加1并转向Step4．

4 仿真分析

为进一步分析基于空间分割和遗传算法相结合的逆运动学算法的性能，利用Matlab设计了测试程序，首先通过给定各关节转角值，利用正运动学计算出机器人头部单元的位姿，然后将其作为已知位姿，分别采用基于空间分割和遗传算法相结合的新算法和单一遗传算法两种方法求运动学的逆解．

基于两种算法的计算结果如表3所示．从表中可以看出，采用新算法计算得出的位置与期望位置非常接近，尤其是子工作空间的优先级越高，计算结果精度越高．例如当期望位姿属于子关节空间S1和S2时，其位置误差为0．其次，采用新算法计算得出的关节角与给定的关节角也非常接近，有利于保持新型煤矿救援机器人的稳定．而单独采用遗传算法不进行空间分割，虽然计算得出的位置和期望位置很接近，但是得出的关节角与给定的关节角相差太大，每个关节都需要转动，这样对保持机器人稳定是不利的．出现上述结果，原因在于采用单一遗传算法的搜索空间大，无法保证收敛到全局最优解．此外，由于新算法实现了运动学逆解的差别化搜索，即根据不同的目标位姿，算法在不同的空间内搜索运动学逆解．因此工作空间的优先级越高，新算法的搜索时间就越短，实时性就越好．

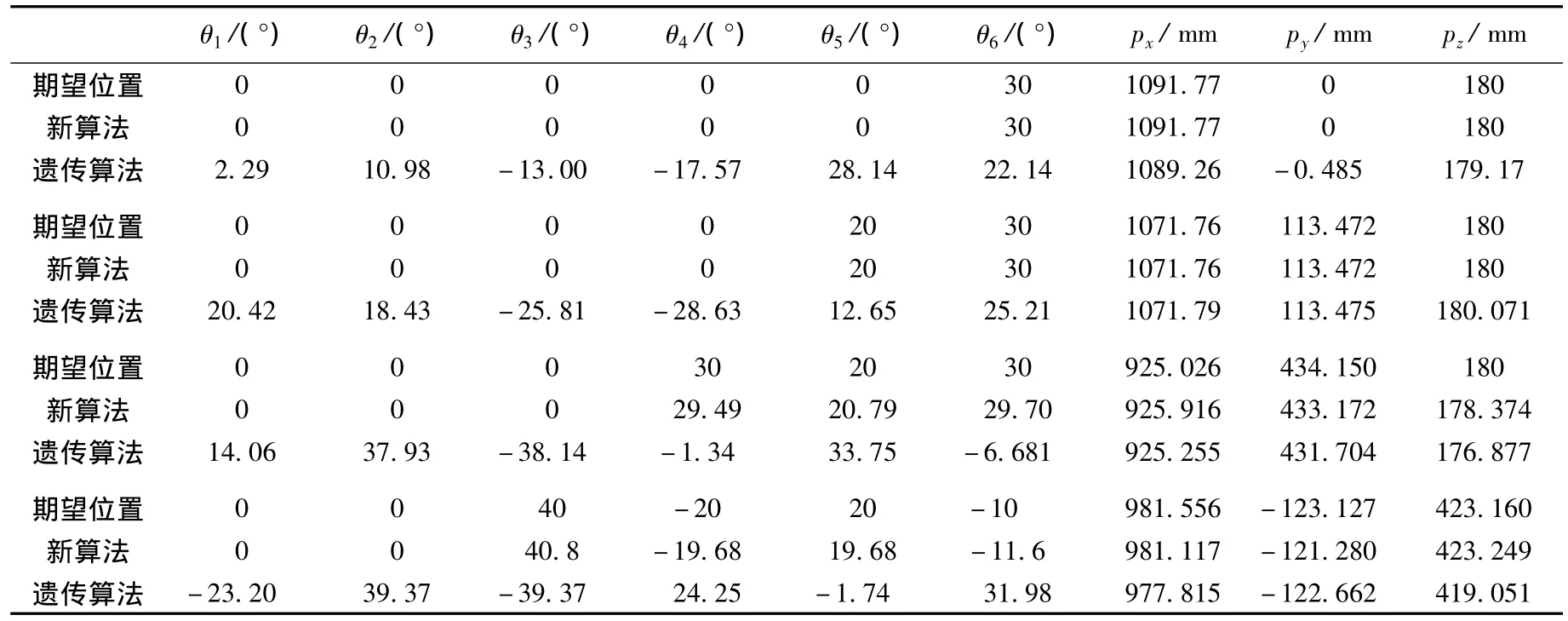
表3 基于两种算法的逆运动学计算结果

5 结论

1)针对新型煤矿救援机器人的结构特点，提出采用一种空间分割和遗传算法相结合的新算法求解机器人的逆运动学．

2)针对基于遗传算法的逆运动学搜索空间大，无法收敛到全局最优解的不足，提出了一种新的空间分割方法．该方法是在离线状态下，利用正运动学对机器人的关节空间和对应的工作空间进行二次分割，解决了基于遗传算法逆运动学搜索空间的灵活配置问题．

3)仿真实验表明，采用空间分割和遗传算法相结合的新算法求得的运动学逆解更加接近真实解，满足以最小的转动代价实现机器人头部单元姿态调整运动的要求，并有利于保持机器人的稳定．

4)所提的新算法也可以应用到其他串联机器人的逆运动学研究．

［1］GUPTA K C，KAZEROUNIAN K．Improved numerical solutions of inverse kinematics of robots［C］//1985 IEEE International Conference on Robotics and Automation．Chicago:［s．n．］，1985:743－748．

［2］TAKAHASHI T，KAWAMURA A．The high-speed numerical calculation method for the on-line inverse kinematics of redundant degree of freedom manipulators［C］//6thInternational Workshop on Advanced Motion Control．Nagoya，Japan:［s．n．］，2000:618 －623．

［3］DAI Y Q，LOUKIANOV A A，UCHYIAMA M．A hybrid numerical method for solving the inverse kinematics of a class of spatial flexible manipulators［C］//Proceedings of the 1997 IEEE International Conference on Robotics and Auomation．Albuquerque，New Mexico:［s．n．］，1997:3449 －3454．

［4］TCHON K．Optimal extended jacobian inverse kinematics algorithms for robotic manipulators［J］．IEEE Transactions on Robotics， 2008，24(6):1440 －1445．

［5］TCHON K，JAKUBIAK J．An extended jacobian inverse kinematics algorithm for doubly nonholonomic mobile manipulators［C］//Proceedings of the 2005 IEEE InternationalConference on Robotics and Automation．Spain:［s．n．］，2005:1548 －1553．

［6］谢宗武，孙奎，刘宏．扩展雅可比方法的冗余度机器人逆运动学应用［J］．哈尔滨工业大学学报， 2009，41(5):34－ 36，85．

［7］马化一，张艾群，张竺英．一种基于优化算法的机械手运动学逆解［J］．机器人， 2001，23(2):137－141．

［8］于振中，闫继宏，赵杰，等．超冗余移动机械臂逆运动学快速求解［J］．北京邮电大学学报:自然科学版， 2009，32(5):55－59．

［9］阳小涛，杨克俭．CCD算法及其在逆运动学中的应用与实现［J］．重庆工学院学报:自然科学， 2008，22(5):65－68．

［10］YANG Yugui，PENG Guangzheng，WANG Yifeng，et al．A new solution for inverse kinematics of 7－DOF manipulator based on genetic algorithm［C］//Proceedings of the IEEE International Conference on Automation and Logistics．Jinan，China:［s．n．］，2007:1947 －1951．

［11］ZHANG Yonggui，XIE Liming，SHEN Hao，et al．Simulation on whole inverse kinematics of a 5R robot based on hybrid genetic algorithm［C］//Proceedings of the Eighth International Conference on Machine Learning and Cybernetics．Baoding，China:［s．n．］，2009:1840 －1845．

［12］ZHOU Youhang，TANG Wenzhuang，ZHANG Jianxun．Algorithm for multi-joint redundant robot inverse kinematics based on the bayesian-BP neural network［C］//2008 International Conference on Intelligent Computation Technology and Automation． Xiangtan， Hunan:［s．n．］，2008:173 －178．

［13］BINGUL Z，ERTUNC H M，OYSU C．Comparison of inverse kinematics solutions using neural network for 6R robot manipulator with offset［C］//2005 ICSC Congress on Computational Intelligence Methods and Applications．Istanbul:［s．n．］，2005:1－5．

［14］TAROKH M，KIM M．Inverse kinematics of 7－DOF robots and limbs by decomposition and approximation［J］．IEEE Transaction on Robotics， 2007，23(3):595－600．

［15］孙奎，谢宗武，王建宇，等．舱外航天服手臂的逆运动学解法［J］．哈尔滨工业大学学报， 2010，42(1):60－ 63，68．

Inverse kinematics for special motion of a new mine rescue robot

LIU Gang，LIU Yu-bin，ZHAO Jie，ZHU Lei

(State Key Laboratory of Robotics and System，Harbin Institute of Technology，150001 Harbin，China，liuxing338@163．com)

Aiming at the special motion(position and posture adjustment)of the head link of a new mine rescue robot，a novel algorithm based on the combination of spatial decomposition and genetic algorithm(GA)was proposed to solve inverse kinematics of the robot．This algorithm can realize prospective position and posture with the lowest turning cost and keep the robot stable．The two-step spatial decomposition method is presented and it overcomes the defects of big searching space and not converging to the global optimum solution using a GA algorithm．Simulation results show that the position and posture error derived using the new algorithm is smaller and the joint angles are closer to real values．The new algorithm can satisfy the motion requirement of head link of the new mine rescue robot．

rescue robot;inverse kinematics;spatial decomposition;genetic algorithm

TP242

A

0367－6234(2011)09－0042－05

2010－06－19．

国家高技术研究发展计划资助项目(2007AA041501)．

刘 罡(1977—)，男，博士研究生;

赵 杰(1968—)，男，教授，博士生导师．

(编辑 杨 波)