12C18O和13C16O分子X1∑+基态的完全振动能谱和同位素位移
刘杰超,马永健,窦 亮
(深圳大学 物理科学与技术学院,广东深圳 518060)
红细胞寿命缩短是导致贫血的原因之一,但是造成红细胞寿命缩短的原因比较复杂,目前尚未完全清楚。如果能即时判断红细胞寿命是否缩短,为临床即早进行治疗,缓解病情提供帮助。研究[1]证实,用呼气中CO浓度可判断红细胞寿命是否缩短。故利用稳定同位素标记的一氧化碳12C18O和13C16O进行呼气试验,可准确探测呼气中CO的浓度。测量稳定同位素的传统方法是质谱法,但质谱仪费用昂贵,操作复杂。如果能详细了解同位素标记的分子12C18O和13C16O相对于12C16O的光谱移动(即同位素位移),则可能建立一种通过测光谱来测定12C18O和13C16O的方法,大幅减化操作过程,减少费用。12C16O分子X1∑+基态的实验振动光谱已有文献[2]报道,但12C18O和13C16O的振动能谱却未见相关报道。
对于CO这样的多电子双原子分子体系,常用的研究能谱量子力学变分理论从头计算法(Abinitio)比较复杂[3],而且大多数使用单电子轨道近似、固定核近似(Born-Oppenheimer近似)[4-6]等物理模型。在这些模型中,多次使用变分参数,致使计算结果的精确性受到很大影响。本工作拟根据实验已经获得的12C16O分子X1∑+基态精确的低振动能谱,结合代数方法(Algebraic Method,AM)和Herzberg的同位素效应理论,计算12C16O分子X1∑+基态的完全振动能谱和同位素分子12C18O和13C16O的各项光谱常数,比较12C18O和13C16O与12C16O同级能级之间的同位素位移,为相关研究提供参考。
1 理论与方法
1.1 AM方法理论
对于多电子体系,精确的量子力学计算非常复杂。利用这种繁杂的方式得到非常精确可靠的能谱是很困难的。虽然实验上已经积累了很多分子电子态的部分振动能级光谱数据,但对于大多数分子电子态来说,其完全振动能谱的实验光谱数据还非常缺乏。如何用已知实验数据得到目前实验上尚未得到,且其他理论也难以得到的精确可靠的分子电子体系的完全振动能谱{Eυ},是件很值得研究的事情。
AM的基本思想如下。1)由于将振动本征能量同本征量子态联系在一起的解析关系式是振动能级公式,对于分子电子态的全程振动范围而言,都可以通过能级表达式将本征能量同振动光谱常数集合与本征量子态解析地正确联系在一起。2)对于给定分子电子态而言,已知的部分振动能级的各种组合都将分别构成其完全振动能谱集合{Eυ}的一个能级子集合[Eυ],而任一子集合中的每一个振动能级都完全满足解析振动能级表达式。3)如光谱实验或严格的量子力学计算足够精确,则完全振动能谱的一切振动信息就包含在已知的子集合[Eυ]中。但在很多情况下,对于给定的分子电子态而言,由于实验方法或量子力学处理所产生的很难避免的误差,而导致测得的某些实验数据或算得的某些振动能级也带有误差。所以,并非所有的子集合中的每一个振动能级Eυ所对应的振动光谱常数集合都具有相同的精确度。因此有必要建立一定的物理方法并寻找一定的物理判据,从一组己知的振动能级中将能够正确代表该电子态的真实振动光谱常数集合遴选出来。4)利用遴选出来的正确振动光谱常数集合代入表征完全振动能谱的能级表达式求得该分子电子态的完全振动能谱{Eυ}的精确数据。
以上即是AM方法研究双原子分子体系电子态的完全振动能谱{Eυ}所依据的基本思想。其核心在于所建立方法的严格性和如何选择能够代表完全振动能谱的正确能级子集合[Eυ]。
1.2 方法
在分子的电子态确定后,理论上该电子态的分子振转能量可以通过求解原子核运动的Schrödinger方程得到。哈密顿量中势能函数不同,可以得到不同近似程度的振转能量及其表达式。双原子分子常用的势能函数有简谐振子函数(SHO)[7]、Morse函数[8]、HMS势能函数[9]和Murrell-Sorbie势能函数[10-12]等。构造这些经验势能函数要用到一些实验参数,所以势能函数本身的精确度受到这些实验数据精度的影响。双原子分子体系核运动的非相对论径向Schrödinger方程表达式如下:

(1)式中,h为普朗克常数;μ为双原子体系的折合质量;R为核间距;V为双原子分子的核运动势能;J为转动量子数;Λ是体系电子的总角动量L在Z轴分量的本征值;Ψ为双原子体系电子的波函数;E为振转能量的本征值;υ为振动量子数。求解这个微分方程,可以得到双原子分子的振转能级。利用Sun等[13-14]建立的以非谐振子模型为基础并结合量子力学的二阶微扰理论,得到双原子分子的振转能量表达式如下:


(2)式中,ω0、ωe+ωe0、-ωexe、ωeye、ωeze、ωete、ωese和 ωere为非谐性振动常数 ;ωe0是对谐性振动常数ωe的修正项;υ为振动量子数;Bυ为振动态υ中的转动常数;Dυ为振动态υ中表示离心力影响的平均转动常数。对于确定的双原子分子电子态,振动能量远远大于转动能量[7],因此在忽略转动能级贡献的情况下,非相对论核运动振动能谱的解析表达式为:

(3)式中,ω0和 ωe0是微小量,它们在计算高阶振转能级时有不可忽略的贡献。用AM方法计算振动光谱常数和完全振动能谱的基本出发点是将正确的微扰振动能级解析式(3)式写成矩阵形式[13]:

其中振动光谱常数的向量矩阵X和振动能量矩阵E分别表示为:

上式中,ωe'=ωe+ωe0,A为含有n×8个矩阵元的系数矩阵,其矩阵元的形式为Aυk=(υ+)k,k=0,1,2,3,4,5,6,7。对于一个双原子分子确定的电子态,若已知M(M≥8)条低振动能级[Eυ],便可从中选出8条振动能级作为已知振动能级许多子集合中的一个来构成振动能量矩阵E,进而通过代数方法,得到一组振动光谱常数[ω0,ωe',-ωexe,ωeye,ωeze,ωete,ωese,ωere] 。将其带入(3)式中,即得到体系的一组完全振动能谱Eυ。而根据振动能谱的物理性质,一套能够表示一个确定电子态的完全振动能谱的光谱常数应满足以下性质[13-14]:
(5)~(9)式是挑选代表体系完全振动能谱Eυ的最佳物理表象的判据条件。(5)式和(8)式表示最高振动能级的收敛极限,对于分子长程无能垒的情况,De对应体系的两原子相距无穷远时的平衡离解能;(6)式和(7)式表示在离解极限处相邻能级所要满足的物理条件;(9)式表示AM能级和实验能级要高度吻合。由此可从部分已知的精确低振动能级[Eυ]中找到满足判据条件(5)~(9)式的实验振动能级的最佳子集合,从而获得一组能够代表体系真实振动信息的精确振动光谱常数及该电子态的正确的完全振动能谱Eυ。这就是获得双原子分子电子态的精确振动光谱常数和完全振动能谱的AM方法。
2 结果与讨论
2.1 AM方法确定的12C16O分子X1∑+基态的完全振动能谱
根据实验测出的12C16O分子X1∑+基态的低振动能谱(υ=0~37)[2],即可选能级数目 Μ=38。将AM方法得出的完全振动能谱和由文献[2]提供的低振动能谱列于表1。
由表1可以看出,AM方法计算出的完全振动能谱在低能级时与实验值吻合,满足判据条件(9)式,说明该方法在计算双原子分子振动能谱中的可靠性。已知12C16O分子X1∑+基态的离解极限为De=90 544.760 0 cm-1[2,15]。当振动量子数υmax=77时,用AM方法得出的振动能级E=90 542.734 4 cm-1,已经很接近其离解极限,相对误差仅为2.237×10-5。当时υ=78,E=90 496.799 0 cm-1,已经出现收敛迹象 ,Eυmax-Eυmax-1=3.707 4 cm-1,已经足够小,满足判据条件(5)~(9)式。计算结果表明,在实验振动能谱Eυexp的精确性可靠的情况下,用AM方法得出了相当精准的12C16O分子X1∑+基态的完全振动能谱。
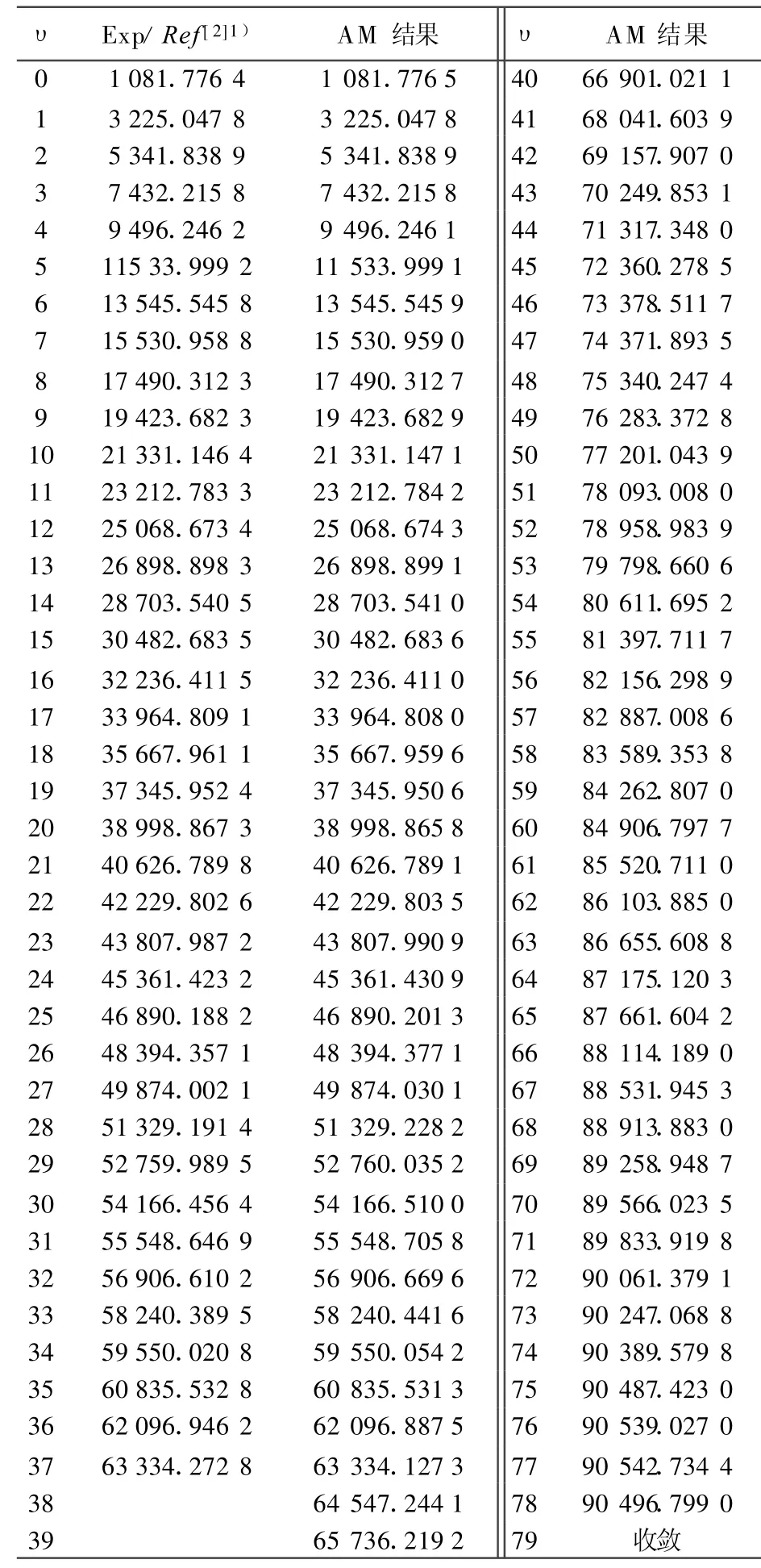
表1 12C16O分子X1∑+基态振动能谱的AM计算结果与实验结果的比较 cm-1
2.2 12C18O和13C16O光谱常数和振动能级的同位素效应
根据Herzberg的同位素效应理论[7],由同位素分子的折合质量之比,可以确定一个同位素参数ρ,通过该参数可以将同位素分子的相关光谱常数联系起来。

(10)~(13)式中,μ为CO分子的折合质量,其上标i为同位素分子。根据(10)~(13)式,利用AM方法得出的12C16O的振动光谱常数,计算出了同位素分子12C18O和13C16O的光谱常数,并得出它们的振动能谱。12C16O、12C18O和13C16O的光谱常数和同位素位移列于表2和表3。
3 结 论
对于12C16O分子X1∑+基态[16],根据实验测出的部分精确的低振动能级,就可以用AM方法求得该电子态的完全振动能谱Eυ。这在一定程度上弥补了实验方法不能测出高振动激发态能级的缺陷。本工作采用AM方法计算出12C16O的光谱常数,并结合Herzberg的同位素效应理论,确定了12C18O 和13C16O分子 X1∑+基态的振动光谱常数,进而计算出了它们的振动能谱。由计算结果可以看出,相对应的同级的光谱常数有明显的差别(表2),从而导致了它们振动能谱的不同,即产生了同位素位移(表3)。该同位素位移的计算结果为探讨通过测光谱的方法来测定CO同位素分子的应用技术提供了参考依据。

表 2 CO同位素分子X1∑+基态的振动光谱常数比较 cm-1
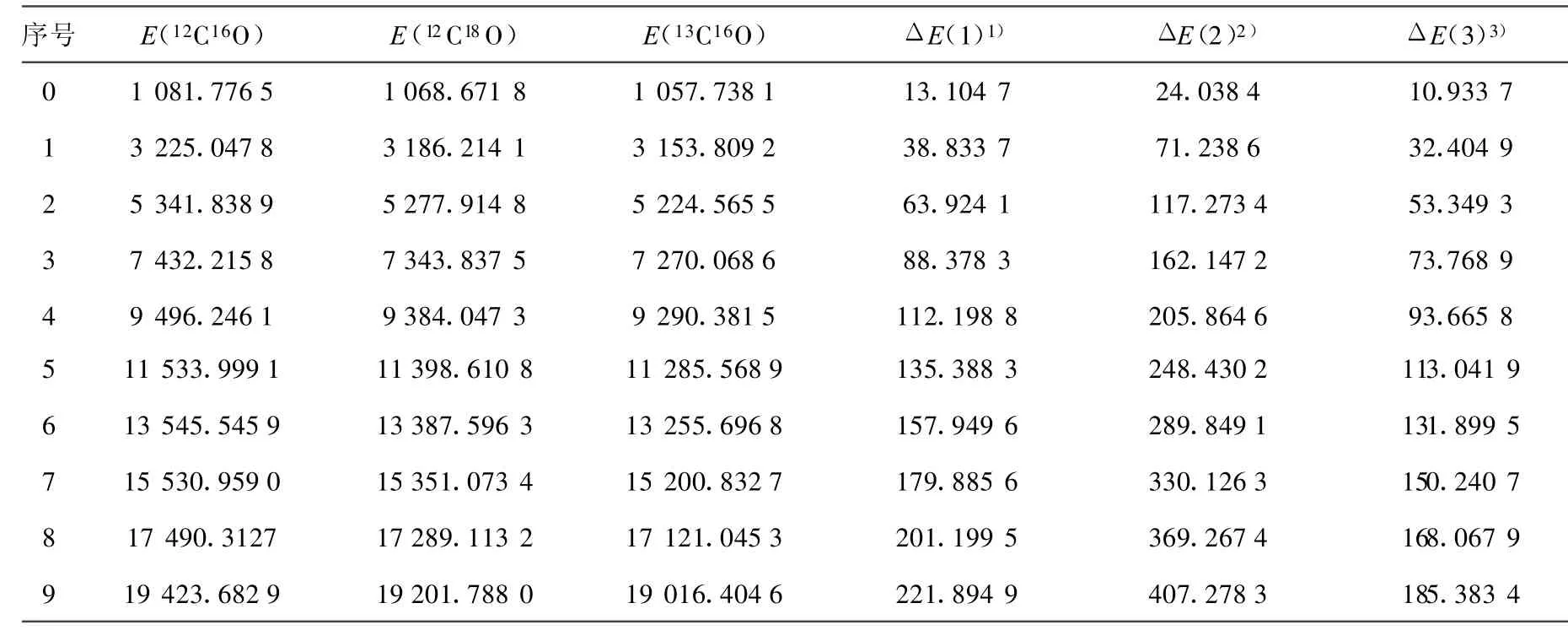
表3 CO同位素分子X1∑+基态振动能谱的同位素位移比较 cm-1
[1] Furne JK,Sp ring field JR,H o SB,et al.Simp lification of the end-alveolar carbon monoxide technique to assess ery th rocy te survival[J].JLab Clin Med,2003,142:1.
[2] Telle H,Telle U.A simp le numerical treatment of the RKR potential integrals and its application to12C16O(X1∑+)[J].JMol Spectrosc,1981,85:248.
[3] 徐光宪,黎乐民.量子化学基本原理和从头计算法[M].北京:科学出版社,1985.
[4] 徐克尊.高等原子分子物理学[M].北京:科学出版社,2000.
[5] 徐亦庄.分子光谱理论[M].北京:清华大学出版社,1988.
[6] Mchale JL.Molecular Spec troscopy[M].New Jersey:Prentice-Hall,1999.
[7] Herzberg G.Molecular spectra andmolecular structure I:Spec tra of diatomic molecu les[M].New York:Van Nostrand Company,Inc,1950.
[8] 周公度,段连运.结构化学基础[M].北京:北京大学出版社,2008.
[9] Huxley P,Murre ll JN.G round-state diatomic potentials[J].JChem Soc Faraday Trans:II.1983,79:323-328.
[10]朱正和,俞华根.分子结构与分子势能函数[M].北京:科学出版社,1997.
[11]Murrell JN,Sorbie KS.New analytic form for the potential energy curves of stab le diatomic states[J].J Chem Soc Faraday Trans:II,1973,7:1 552-1 557.
[12]Huxley P,Knowels DB,Murrell JN,et al.G roundstate diatom ic potentials.Part 2:Van der Waals molecu les[J].JChem Soc Faraday Trans II,1984,80:1 349-1 361.
[13]Sun Weiguo,H ou Shilin.Studies on the Vibrational and Rovibrational Energies and Vibrational Force Constants of Diatomic Molecular States U-sing A lgebraic and Variational Methods[J].J Mol Spectrosc,2002,215:93-105.
[14]孙卫国,侯世林.双原子分子体系的振动结构研究[J].原子核物理评论,2002,19(2):91-94.
[15]Huber KP,Herzberg G.Molecular Spectra and Molecular Structure(IV),Constants of Diatomic Molecules[M].New York:Van Nostrand,1979.
[16]朱正和.原子分子反应静力学[M].北京:科学出版社,1996.

