水平单向及多向载荷下单桩响应的数值研究

苏 栋，袁胜强，李锦辉

1)深圳大学土木工程学院，深圳518060;2)河南徐辉建筑工程设计事务所，郑州450008;3)哈尔滨工业大学深圳研究生院，深圳518055

桩基通常以承受竖向载荷为主，但在某些情况下，可能受较大的水平载荷作用，如地震作用下民用建筑的桩基、在波浪冲击下海上钻井平台的桩基以及风载荷作用下电线塔的桩基等.这些水平载荷大多数是多方向的，其大小和方向都在不断变化.目前，不少学者对水平受荷桩进行了较多研究［1-7］，但都集中在单向载荷，对水平多向载荷的研究较少.本研究利用大型有限元分析软件ABAQUS，建立了砂土中单桩的三维弹塑性数值分析模型，通过三轴实验确定土体相关参数，研究水平单向载荷作用下桩头自由和固定单桩的响应特性，并研究了多向加载路径对单桩承载力的影响.

1 分析模型

本研究采用大型通用非线性有限元分析软件ABAQUS.由于前期已进行室内模型试验，故数值分析以实验模型为原型，与实验结果进行对比分析.实验中实验箱为铸铁圆桶，内径500 mm，高700 mm;桩为圆形不锈钢管桩，直径38 mm，壁厚0.8 mm，桩入土深度为500 mm，加载点位于土面上200 mm，只施加水平力，不施加弯矩.在数值模拟中，实验箱不直接建模，而是对边界上的土体单元进行位移限制，以模拟实验箱对土体的约束.由于桩管壁较薄，若按薄壁管建模，则在处理桩与土的接触，以及桩身的网格划分方面比较困难，因而数值分析模型采用实心桩体，通过调整弹性模量保证桩体的抗弯刚度和试验模型一致.

图1为建立起来的三维数值分析模型.由于桩土之间的水平相互作用主要集中在浅层位置，所以土体上部网格划分较密，下部网格划分较疏，以减少计算量.同样，较近部分土体受桩的影响较直接，变形较大，所以网格划分较密，以满足计算和精度的要求，离桩较远的土体网格划分较稀疏，以减少计算量.

采用非协调单元C3D8I分析模型中的桩和土体，以避免出现压缩闭锁现象.非协调单元将附加自由度引入到线性单元中，避免单元交界处的位移场出现重叠或裂隙.桩土之间采用主从面接触，桩面为主面，土面为从面.在实际加载过程中桩体与桩周砂土是不分离的，所以在数值分析中让桩土单元接触后不分离.桩土主从面之间的摩擦系数采用0.2，以罚函数处理接触面的切向关系，接触面的法向采用硬接触方式，在外载荷的挤压下，桩面穿入外部土体，一旦接触不允许分离.

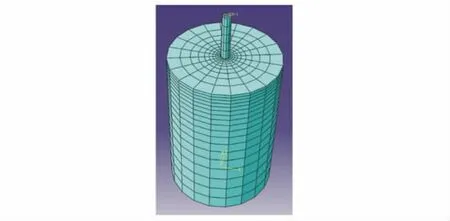
图1 分析模型Fig.1 Analysis model

2 土体本构模型及其参数

采用ABAQUS内置的弹塑性d－p模型模拟砂土行为，模型的参数有:角度β(p'－q平面内临界状态线与p'轴的夹角)、剪胀角ψ(ψ=β时，材料服从关联流动法则)以及材料参数K.

为确定角度β，完成了一批不同围压下砂土的三轴压缩实验.试验在GDS三轴仪上进行，材料为室内模型实验所用的平潭砂，其最大孔隙比为0.855，最小孔隙比为0.542.试样制备采用干落法，制得的试样直径为48.3 mm，高度为100 mm，相对密度约40%.共进行了9个实验，根据实验测得的应力和应变曲线确定每个实验的临界状态点，并将临界状态点的应力状态(p'，q)画在p'－q平面上，利用最小二乘法拟合出临界状态线，得到临界状态线与p'轴的夹角为47.9°.假定材料服从关联流动法则，所以剪胀角ψ也取47.9°，材料参数K取1.另外砂土的弹性模量取22 MPa，泊松比取0.35，其中弹性模量为土体深度中部的数值，根据文献［8］可确定土体的剪切模量G，

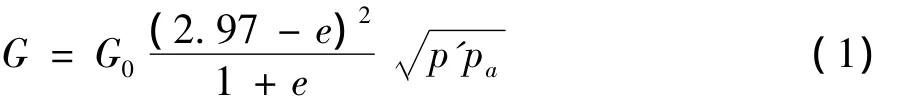
其中，G0为材料常数;e为土体的孔隙比;p'为平均有效正应力;pa为大气压力.由剪切模量和泊松比可计算出弹性模量.

3 单桩单向加载的数值模拟

与室内模型实验一样，控制桩头加载点 (高出土面200 mm)匀速沿X方向运动10 mm(如图1).该过程中允许桩头自由转动.加载结束后，取出数值模拟结果，与室内模型实验结果进行比较.图2为计算和实验得到的桩头水平力与位移的关系曲线.由图2可见，计算结果和室内实验吻合较好.两条曲线都表现出明显的非线性特征，随着水平位移的增加，水平力的增幅渐减.当位移为10 mm时，室内实验测得的水平力为270 N，而计算得到的水平力为273 N，两者相差不大.

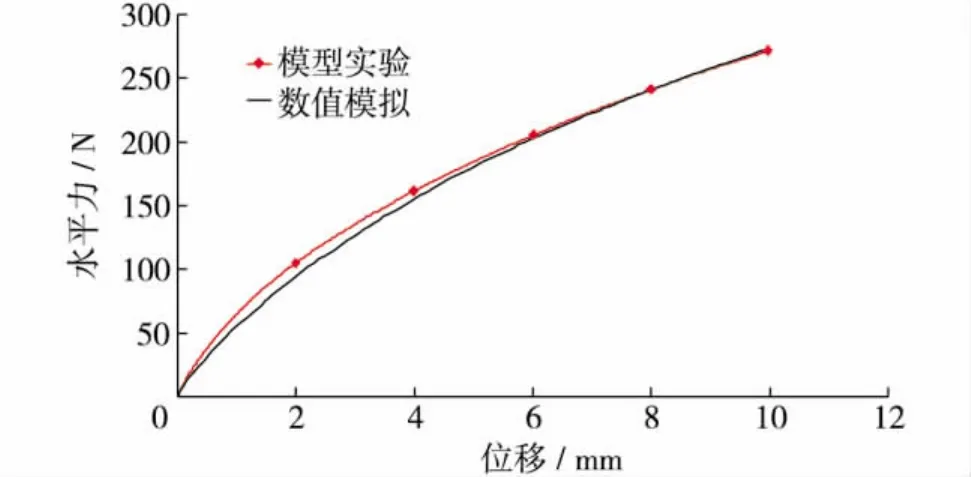
图2 桩头水平力和位移的关系曲线Fig.2 The relationship between horizontal force and displacement at the pile head

在模型实验中，一般只能通过应变传感器测得桩身的应变，从而计算其所受的弯矩，数值计算可得到桩身各单元的弯矩、剪力和位移等数据.桩头位移分别为2.5、5.0、7.5和10 mm 时桩身的弯矩分布如图3.由图3可见，桩身弯矩的分布类似弓形，这是桩头自由的短桩在水平载荷作用下的典型响应.在4个不同时刻，桩身弯矩的最大值出现在土面下约150 mm(约4倍桩径)处，分别为30.2、54.9、73.6和88.7 N·m，弯矩值的增幅低于水平位移的增幅.

桩头位移分别为2.5、5.0、7.5 和10 mm 时桩身位移随深度的变化如图4.由图4可见，桩身位移有一个零点位置，位于土面下320～350 mm处(随着桩头位移的增大而加深)，此点以上的桩身往桩头运动方向弯曲，此点以下的桩身往相反方向有较小位移，即桩身绕着该点旋转.从桩-土相互作用看，零点以上的桩前土体受挤压，承受被动土压力;零点以下的桩后土体受挤压，承受被动土压力.从图4还可看出，当桩头位移为10 mm时，深度为200 mm处的桩体位移为1.4 mm，而深度为500 mm处的桩体位移只有0.6 mm，这两处离桩体位移零点 (土面下350 mm)的距离是相同的，但位移却相差很大，零点以下的桩体位移要明显小于上部的桩体位移.可见在水平载荷作用下，桩体和土体的变形主要集中在较浅层部分，桩的水平承载力往往也和浅层土体的性质密切相关.但由于土体应力水平随深度的增加渐增，对桩的水平抗力也增大，因而深处的土体对桩有一定的嵌固作用，桩身越长，土体对桩的嵌固作用也就越强，桩的抗侧移能力亦越强.

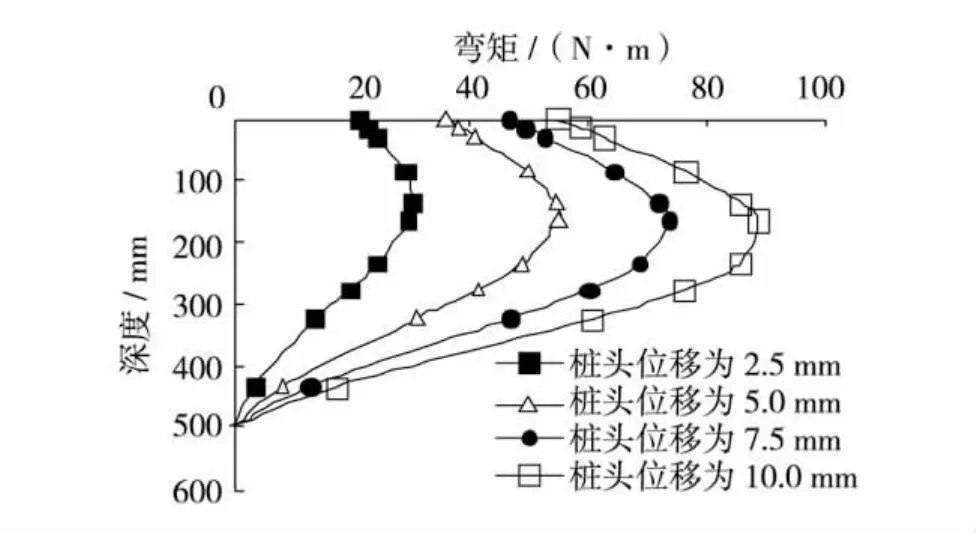
图3 不同桩头位移时桩身的弯矩分布Fig.3 The moment along the pile under different pile-head displacement

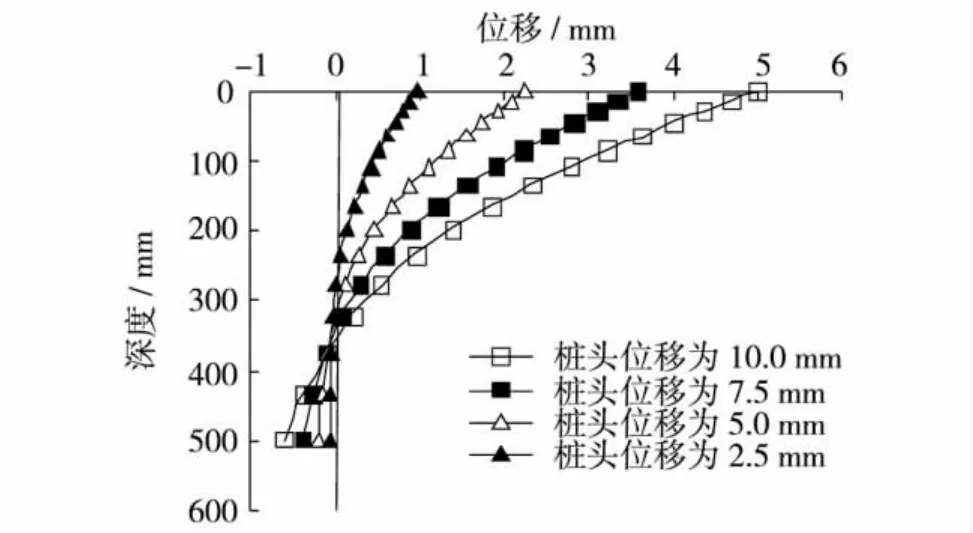
图4 桩身位移随深度变化Fig.4 The variation of pile deflection along the depth

数值模拟相对物理模型试验的另外一个优势是，从中更容易获取加载过程中有关土体变形的信息.桩头位移分别为2.5、5、7.5和10 mm时桩运动前方土面隆起量随径向距离的变化如图5.由图5可见:①土体的隆起量随着桩头位移的增加而增大;②当桩头位移较小时 (2.5 mm)，桩边土体的隆起量最大，随着径向距离的增加，隆起量越来越小;③当桩头位移较大时 (7.5和10 mm)，由于受桩身竖向摩擦的约束，桩边土体的隆起量并不是最大，而是略小于离桩稍远一些的土体;④在3倍桩径 (108 mm)范围内的土体隆起比较明显，范围外的土体隆起量相对较小.

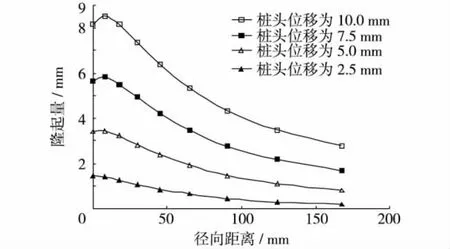
图5 桩前土体隆起量随径向距离的变化Fig.5 The heaving of soil along the direction of pile movement

4 桩头嵌固方式对单桩响应的影响

图6比较了桩头2种不同嵌固方式下得到的水平力和位移关系曲线.由图6可见，水平位移相同时，桩头固定的水平力远大于桩头自由的水平力，当位移为10 mm时，分别为725和273 N，前者是后者的2.65倍.

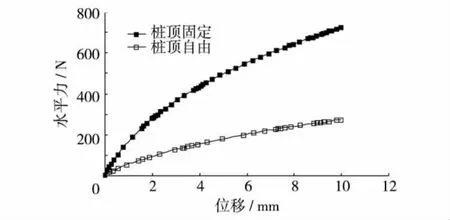
图6 嵌固方式对桩头水平力的影响Fig.6 Influence of restraint condition of pile head on the horizontal force

图7 比较了2种不同桩头嵌固方式下，桩顶位移为10 mm时的桩身弯矩分布曲线.由图7可见:①对于桩头自由的桩，在桩头位置的弯矩为零.而对于桩头嵌固的桩，为使桩头在水平方向运动的同时不发生转动，需要在桩头施加很大的弯矩;②两种不同嵌固方式下桩身弯矩的分布有很大区别，桩头自由的桩，其桩身的弯矩都为正值，即桩身只有背面受拉.而桩头固定的桩，其桩身所受弯矩正负值都有，分界点大约在土面下110 mm处，在此位置上的桩前面受拉，在此位置下的桩背面受拉;③桩头自由的桩，其桩身最大弯矩大致在土面下150 mm处，桩头固定的桩，其弯矩最大值却在桩头处，前者数值为163.6 N·m，后者数值为224.3 N·m，后者比前者大约37%.

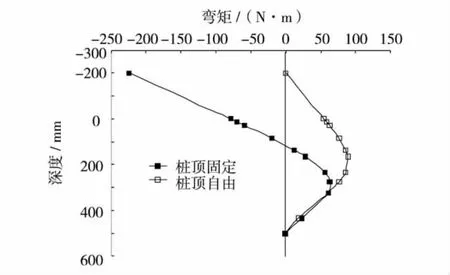
图7 嵌固方式对桩身弯矩的影响Fig.7 Influence of restraint condition of pile head on the bending moment along the pile

图8比较了2种不同桩头嵌固方式下，当桩顶位移为10 mm时，沿桩水平运动方向桩前土体的隆起量随径向距离的变化曲线.从图8可以看出，桩头固定时的隆起量明显大于桩头自由时，影响的范围也更广，前者的最大隆起量为16 mm，约为后者的2倍，这说明桩头固定时桩前土体受挤压程度要比桩头自由时大一些，变形也更大.

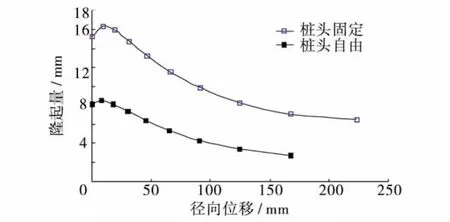
图8 嵌固方式对桩前土体隆起量的影响Fig.8 Influence of restraint condition of pile head on the heaving of soil along the direction of pile movement

综上结果可见，桩头固定的桩，其抗弯刚度大大提高，桩顶弯矩加大，桩身弯矩减小，桩身位移零点位置下移，土体的变形向远处和深处发展，能更充分发挥土的抗力，从而提高水平承载力.

5 多向加载路径对单桩响应的影响

多向加载实验为同时控制桩头加载点的X和Y方向的位移，以研究在多向加载路径下的桩体响应特性.本研究主要模拟3种多向加载路径:圆形(Y方向与X方向位移幅值比α为1)和2种椭圆(Y方向与X方向位移幅值比α分别为0.6和0.2)，每种加载路径都施加了5个周期.

图9(a)、(c)和 (e)分别为3种多向加载方式下计算得到的桩头沿X方向的水平力和位移关系曲线.3种不同加载路径下，X方向的水平力和位移关系曲线具有一些共同特征:①水平力和位移关系曲线都表现出明显的滞回特性;②经过第1周期的加载后，在随后的几个周期中水平力和位移关系曲线都基本稳定下来.但3种不同加载路径和单向加载也有明显区别，主要表现在:① 单向加载下水平力的最大值为273 N，而短长轴比为0.2、0.6和1.0时，水平力最大值分别为270、262和255 N，说明随短长轴比增大，X方向的承载力降低;②在单向加载实验中，载荷最大值出现在位移最大时(X=10 mm)，而在多向加载实验中，X方向的载荷最大值先于位移最大值出现.最大值出现的位置与短长轴比有关.短长轴比为1时，X方向第1周期的最大载荷出现在X方向位移为9.4 mm时;短长轴比分别为0.6和0.2时，最大载荷对应的位移分别为9.7和9.9 mm.为便于比较，图9(b)、(d)和 (f)给出了相同加载路径下模型试验测得的桩头水平力和位移关系曲线.从图9可见，数值分析和实验得到的桩头水平力的总体变化趋势基本一致，即随着短长轴比的增加，X方向的承载力降低，载荷最大值先于位移最大值出现.但它们在数量上有较明显区别，如当短长轴比为0.6时，最大载荷计算值为262 N，与单方向相比降幅约为4.0%，而实验测得的载荷最大值为221.4 N，与单方向相比，降幅约为18%.这可能是由于数值分析中使用的砂土本构模型具有一定局限性造成的.实验中桩受水平多向载荷作用时，由于桩土间的相互作用使桩周部分土体松动、软化，降低了土体刚度.但数值模拟采用软件自带的d－p模型，其弹性模量是恒定的，这样在模拟加载过程中土体的性质没有明显退化，所以数值模拟中随着短长轴比的增加，X方向承载力降低的幅度没有室内实验观察到的明显.此外，在多向加载试验的数值模拟中还观察到:①X方向的桩身弯矩最大值随着短长轴比的减小而增大，而最大值所处的位置，随短长轴比的减小，逐渐靠近单向加载桩身弯矩最大值所处的位置;②桩身剪力的最大值随着短长轴比的减小而增加，并逐渐接近单向加载时的最大值;③在加载过程中，桩头载荷矢量增量的方向始终偏离位移矢量增量的方向 (出现非共轴现象)，并指向圆和椭圆位移路径的内侧，这与文献［9］利用离散元分析所得结果一致.

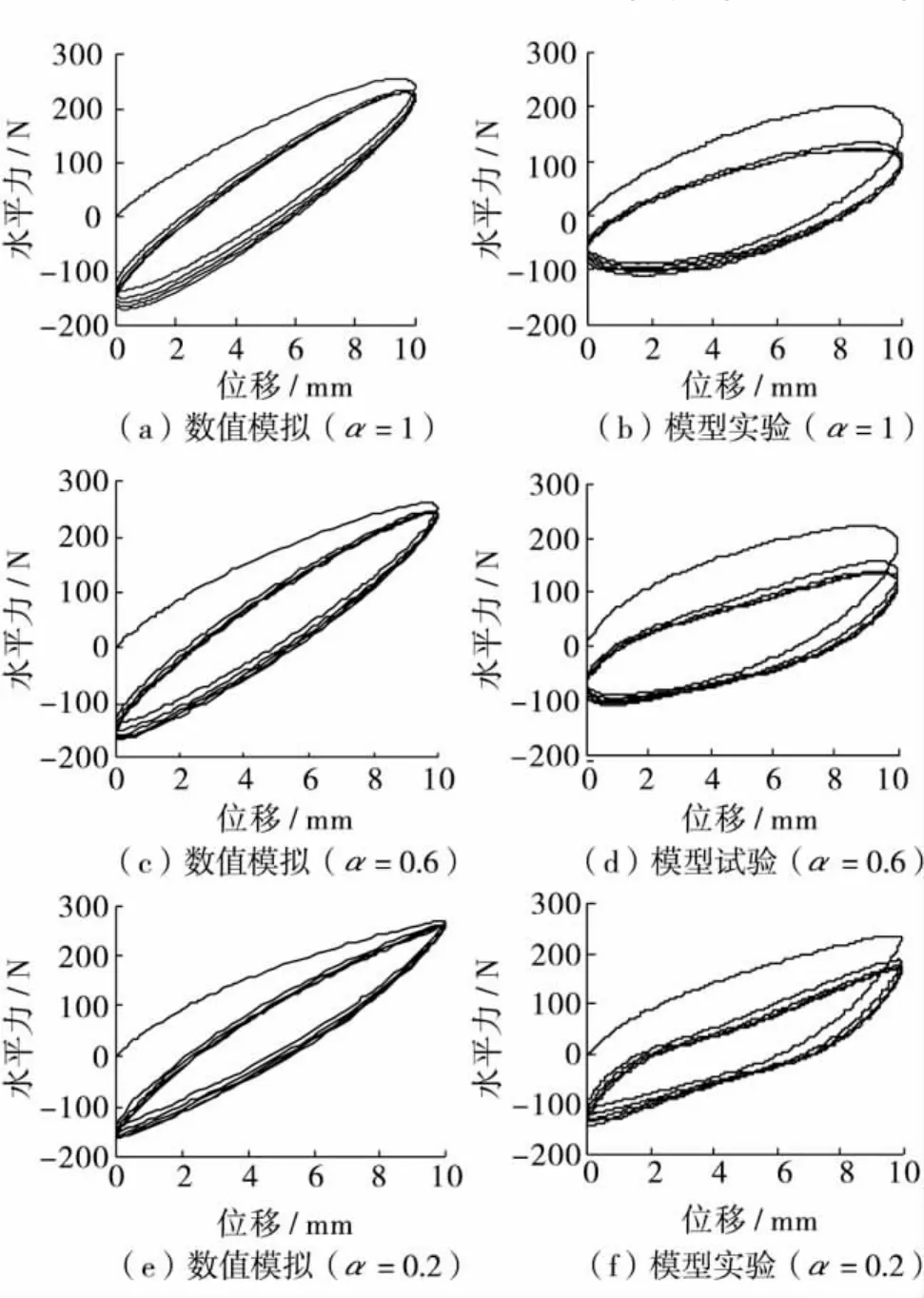
图9 圆及椭圆加载路径下X方向水平力与位移关系Fig.9 The lateral force-displacement relationship along X direction under circular and elliptical loading path

结 语

利用大型有限元分析软件ABAQUS，建立了砂土中单桩的三维数值分析模型，研究了水平单向载荷作用下桩头自由和固定的单桩的响应特性，以及多向加载路径对单桩承载力的影响，由分析可知:①桩头允许自由转动的单桩在单向水平载荷作用下的桩头水平力和位移关系曲线表现出明显的非线性的特点，桩身弯矩分布近似弓形，最大弯矩出现在土面下约4倍桩径处;②桩头允许自由转动的单桩在单向水平载荷作用下桩运动前方土体隆起的最大值不是出现在桩周，而是桩前约0.5倍桩径的土体;③与桩头自由的桩相比，桩头固定的桩抗弯刚度大大提高，桩顶弯矩加大，桩身弯矩减小，桩身位移零点位置下移，土体的变形向远处和深处发展，水平承载力也更高;④ 在沿X方向作相同位移时，由于Y方向加载的影响，多向加载中X方向的水平承载力比单向加载条件下明显减小了，且随着短长轴比的增大，X方向的承载力降低，而载荷最大值出现得更早，这与实验结果一致.

［1］XU Bin，LU Jian-fei，WANG Jian-hua.半无限多层多孔介质弹性空间中单桩在侧向简谐载荷下的动力响应［J］.国际岩土数值与解析方法期刊，2010，34(5):493-515.(英文版)

［2］Ali B.水平载荷作用下砂土中的单桩:由预钻孔旁压试验试验确定p-y曲线［J］.岩土与地质工程，2007，25(3):83-301.(英文版)

［3］王 梅，楼志刚，李建乡，等.水平荷载作用下单桩非线性m法试验研究［J］.岩土力学，2002，23(1):23-26.

［4］Sanjeev K，Latika L，Maher O.水平载荷作用下砂土中单桩非线性响应分析的kh max方法［J］.岩土与地质工程，2006，24(1):163-181.(英文版)

［5］刘汉龙，陶学俊，张建伟，等.水平荷载作用下PCC桩复合地基工作性状［J］.岩土力学，2010，31(9):2716-2722.

［6］赵明华，汪 优，黄 靓.水平受荷桩的非线性无网格法分析［J］.岩土工程学报，2007，29(6):907-912.

［7］乔友刚，吴先敏.水平受荷桩非线性有限元分析［J］.水运工程，2009，4:38-42.

［8］LI Xiang-song.基于与状态相关剪胀性的砂土模型［J］.岩土技术，2002，52(3):173-186.(英文版)

［9］苏 栋，李 霞，李相崧.桩-土水平相互作用的颗粒流数值研究［J］.深圳大学学报理工版，2006，23(1):42-47.