基于样品点优化的变权重组合软件可靠性的仿真研究

范 伟

（重庆理工大学 计算机学院，重庆 400054)

0 引言

软件系统随着人们对软件功能需求的增加而日益庞大和复杂，而越来越严重的软件“虫灾”，让人们意识到软件可靠性的重要性。软件可靠性是指在规定的条件和时间里，软件不引起系统失效的概率。软件质量水平高低的一个重要衡量指标就是软件可靠性指标，指标的评测已经成为一个研究热点，其中利用软件测试失效数据进行可靠性研究是一个重要的分支，从软件失效事件的时间序列角度对软件可靠性进行研究也是一个重要的分支。

传统的基于时间序列软件可靠性评测的模型主要有AR模型、MA模型、ARMA模型、灰色模型及神经网络等。这些模型都有自己的特性，应用了各不相同的预测技术，对于软件失效数据的拟合结果也有一定的精度。然而，在软件开发的过程中，由于影响软件可靠性的因素有很多，因此试图用某个单一的模型进行准确的预测是不可能的。为修正单一预测方法引起的系统性的误差，集中较多信息，综合反映多种预测技术，近年来对于组合预测的研究越来越多，应用的领域也越来越广泛，也取得了不错的效果。

为提高软件可靠性模型预测精度，本文提出一种变权重组合预测模型，并与经过了模拟退火算法优化的BP神经网络（SA-BP）及经过遗传算法优化的最小二乘支持向量机(GA-LSVM)的预测结果进行样本内、外及综合预测能力的比较，验证了该模型的可行性和有效性。

1 变权重组合预测模型

设某一具体软件经测试，共得到连续N个计数期的软件失效样本数据，其中M期数据用于建立可靠性评测模型（M〈N），剩余数据用于模型样本外数据测试；在对该软件可靠性评估时建立n种单一模型，F1,F2,…,Fn,假设：

Yt——该软件第t期内实际累计失效的数据(t=1,2,…)；

Fti——第i种预测方法在第t期内软件累计失效数据的预测值；

Wti——第i种预测方法在第t期的权重

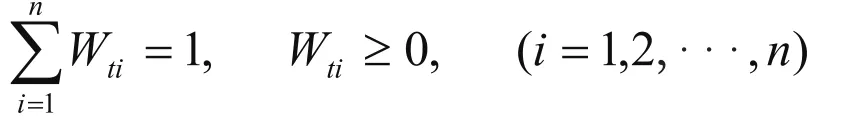
则变权重组合预测模型表示为：

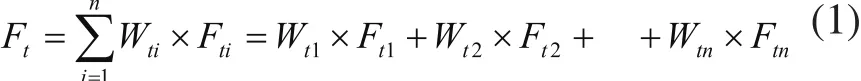
其中，Ft表示第t期该变权重组合模型对该软件累计失效数据的预测值。

与传统的定权重预测模型不同，其特点主要在于组合模型中每一期各单一预测模型的权重系数wti随估算期限变化而变化，而其求解方法也是组合预测模型的关键。

1.1 样本内组合模型各预测方法权重

在软件失效序列第t期（t=1，2，…，M）

若Fti-Yt不完全同号，将n个预测模型分为I1、I2两 类 ， 其 中，则可以找到两个不同的预测模型k，，其中模型k，满足，模型h，满足，则此时在软件失效序列第t期各模型权重为：

由式（2）、（3）可知在样本内，当n个单一预测模型建立后，各单一预测模型的权重系数在每一期样本点的权重都是确定的，但是在不同期样本点所处其值随该模型及其它单一模型的预测精度的不同而可能有所不同，也就是说在样本内各单一预测模型的权重系数是变化的。

1.2 样本外组合模型各预测方法权重

在软件失效数据第t预测期内（t〉M）,组合模型样本外各预测模型权重值为：

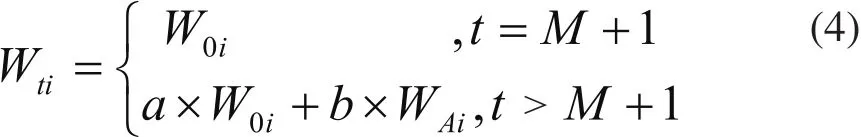
其中，a，b为各单一预测模型样本外组合预测变权重系数对各预测模型样本内与样本外第t期前预测结果的平均权重弹性系数，且a+b=1；

Woi为 各算法在样本点范围内的平均权重：

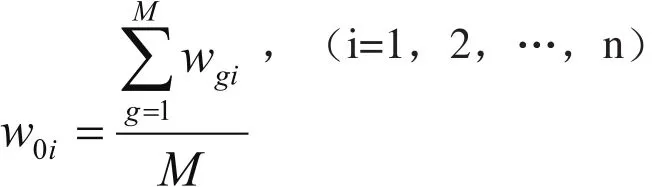
在各单一预测模型建立后该值为常数；

WAi为各算法在样本点外的各预测值的平均权重：

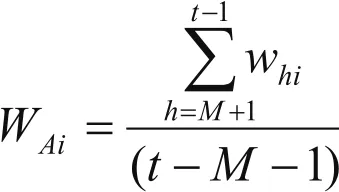
其中第h期预测方法i的权重系数whi的求解方法与样本内数据组合模型权重系数求解方法相同。

由式（5）可知，在样本外的预测中，第一个预测值各预测模型的权重系数是由样本内各单一模型的平均预测精度决定的，在各单一预测模型建立后，该权重系数为一定值，其它期各模型的权重系数则受到各模型样本内的预测精度及样本外的预测精度的影响。虽然woi是一个固定值，但由于WAi是时变的，因此样本外各模型的权重系数也是时变的，影响其值大小的因素有woi、WAi及弹性系数a，b。

2 数值仿真

为对本文提出的组合模型与其他软件失效模型进行比较，采用文献[11]中的一组Musa数据集，对该软件的可靠性进行仿真，具体原始数据如表1所示，其中i为软件测试计数期, Yi为在第i个软件测试计数期内软件累计失效的次数。

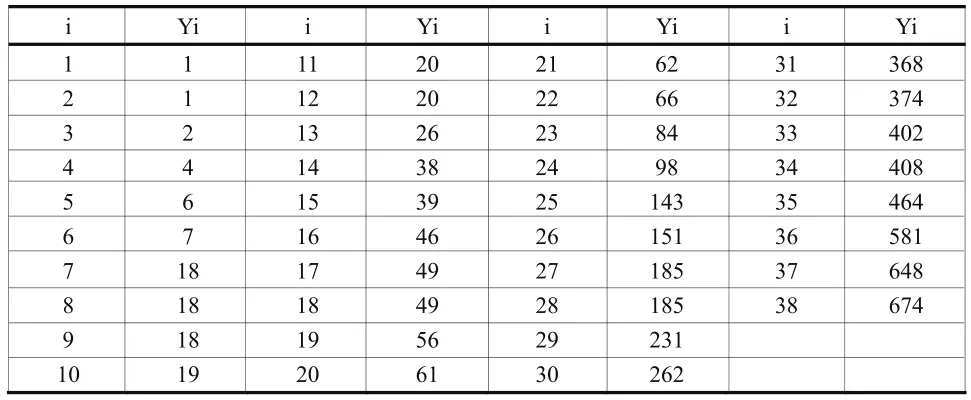
表1 Musa 数据集 （时间单位：分钟）

本文选择经过模拟退火算法优化过的BP神经网络（SA-BP）及经过遗传算法优化的最小二乘支持向量机（GA-LSVM）算法，分别建立该软件的可靠性预测模型。

2.1 SA-BP模型

1）模型输入输出向量处理

输入向量是连续4期软件累计失效数据，输出数据是下一期软件累计失效数据，则将原始所有样本数据分为30组，其中前24组用于样本内预测模型训练，后6组数据作为模型样本外对该模型的泛化能力的检验。并在模型训练前，将所有数据做归一化处理。

2）模型参数设置

由于BP神经网络模型涉及到众多参数，没有经过优化的模型容易陷入局部最优，降低模型精度，为此采用模拟退火算法（SA）对BP神经网络的学习速率lr、动量因子mc及隐含层神经元个数x进行优化，具体步骤如下：

（1）选用Boltzmann机，退火初始温度设置为15000，退火时间间隔为100，温度更新函数选择指数函数，模型终值条件为目标函数值最终变化小于IE-6。

（2）为保证模型的预测精度及范化能力，优化目标函数设为：

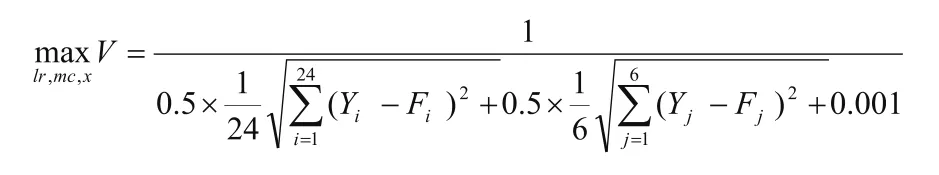
式中，Yi为第i个学习样本的实际值；Fi为第i个学习样本的预测值；Yj为第j个样本外数据的实际值；Fj为第j个样本外数据的预测值；

（3）利用SA算法计算得到优化参数为：lr=0.0078，mc=0.52，x=10

3）将得到的模型参数代入，得到软件失效数据预测结果。

2.2 GA-LSVM模型

该模型输入输出向量设置、预处理过程及参数优化目标函数同上设置，利用遗传算法（GA）对使用径向基核函数的最小二乘支持向量机的调整参数C和径向基函数的宽度σ进行优化。遗传算法设置种群个数为20，进化最大迭代次数为300；交叉概率为0.25；变异概率为：0.01；采用实数编码。优化后参数值C=5182.2，σ=15.3，将参数代入模型计算得到预测结果。

2.3 组合预测模型

在已经建立的SA-BP、GA-LSVM模型的基础上，利用本文建立的变权重组合预测模型进行预测。

设置权重弹性系数a=0.5，b=0.5，得到样本内及样本外各单一模型的30组权重值，并计算组合模型拟合结果。

2.4 模型性能比较

预测结果表明三种预测模型都有一定的预测精度，预测结果都与软件原始失效数据相趋同。为判明模型优劣，利用均方差SME及相对平均误差RAE对上述模型性能进行比较，如表2所示。

表2 各种预测模型性能比较

其中，

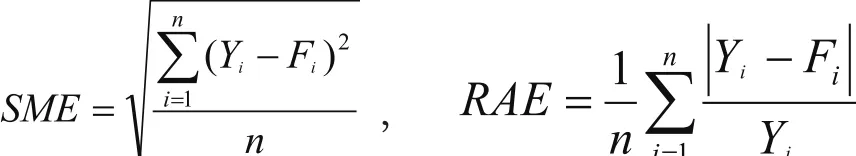
Yi为第i个样本的实际值；Fi为第i个样本的预测值。

由表2可知，在样本内SA-BP预测精度比GALSVM模型要高很多，在样本外，SA-LAVM显然要弱于模型GA-LSVM,说明SA-BP样本内学习能力较强，而样本外泛化能力相对较弱，将样本内与样本外数据综合考虑，SA-BP模型要弱于GALSVM模型。而本文提出的变权重组合模型，在样本内其预测精度比SA-BP高，在样本外其泛化能力也较GA-LSVM强，综合预测能力在三个模型中最优，对软件失效数据拟合误差最小，说明该模型的预测性能较好，从而为软件可靠性评估提供一种更为有效的评测模型。

3 结论

本文建立了一种基于样本点优化的变权重组合软件可靠性评测模型，该模型中各单一模型的权重系数都会根据各样本点的预测结果做出相应调整。在样本内，各样本点的权重系数会根据方差倒数法选择最优权重，而在样本外，随着预测数据的增多，样本外各单一预测模型的权重系数会根据各模型样本内的预测精度，及样本外各单一模型之前的样本外的预测精度进行相应调整。通过实证分析，该模型无论在样本内、样本外，还是综合考虑对软件失效数据的拟合性，能都显著优于SA-BP、GA-LSVM这两种预测性能较好的机器算法，因此在软件可靠性分析中具有较高的推广价值。

[1] 马飒飒,宁如云.基于贝叶斯估计的软件可靠性综合评估模型[J].兵工学报,2008,(04):440-445.

[2] 雷航,马成功.Markov模型的软件可靠性测试充分性问题的研究[J].电子科技大学学报,2010(1):101-105.

[3] 贾治宇,康锐.软件可靠性预测的ARIMA方法研究[J].计算机工程与应用,2008,(35):17-21.

[4] 吴勤,侯朝桢,原菊梅.基于Kohonen网络的软件可靠性模型选择[J].计算机应用,2005,(10):2331-2333.

[5] 马飒飒,冯哲,赵守伟.基于SVR的软件可靠性预测模型研究[J].计算机工程与应用,2007,(13):120-123.

[6] 靳昂,江建慧,楼俊刚,张蕊.基于灰色模型的软件可靠性建模[J].计算机应用,2009,(03):690-694.