基于神经网络的集中供热智能仿真系统设计

孙 兵

（南通纺织职业技术学院，南通 226007）

0 引言

集中供热系统就是将大量的热用户通过热力网连接起来，由统一的热源提供所需热量的供热系统。我国集中供热从50年代开始起步，虽然为节约能源、减少环境污染、改善人民生活发挥了重要作用，但目前整体管理和技术水平还较低，存在供热品质差、缺乏控制与节能手段等问题[1]。实现供热系统优化设计与运行是供热行业发展的必然趋势，由于供热系统不能完全用数学模型来描述，其中需要大量的经验知识乃至知识的推理，建立包含知识模型在内的广义模型不可避免，基于广义模型的仿真必然是智能仿真。智能仿真将人工智能和系统仿真技术相结合，大量使用专家系统、模式识别、知识工程、模糊推理、神经网络等人工智能手段，从系统可实现性、经济性、安全性、实时性等角度考虑，能更准确模拟特定对象。本文采用智能仿真方法进行了集中供热系统的仿真研究，与一般供热系统仿真模型相比较，所建立的快速神经网络模型的创新之处在于：该模型将通常的神经网络结构分成线性和非线性两部分，分别采用不同的辨识方法作用于相应的结构上，能够加快训练速度，提高辨识精度，更有利于实现供热自动控制系统的优化设计。

1 集中供热智能仿真系统结构与功能

供热智能仿真系统在设计上首先对供热系统中主要环节（管道、节点）建模，管道形成热网，节点包括房间、楼宇、热力站等实体[2]。然后根据室外温度、热源情况，对系统典型环节做动、静态仿真，并按已知热网情况调度热力站或根据室外温度调度热源，确定优化运行方案，模拟系统实际运行。

1.1 供热智能仿真系统总体方案

供热智能仿真系统的总体方案如图1所示，其中主要内容有：1）智能仿真模型：除可用数学模型外，还可建立基于知识的对象模型，以提高仿真模型的描述能力，扩大仿真模型的应用范围，增强仿真系统的柔性；另外，面向对象的图形建模方法为用户建模带来了极大的方便，利用仿真建模的专业知识构建典型模块，根据用户需求及环境条件进行模型选取、赋值、组装、构造及验证。2）智能仿真算法：根据选定的模型来确定算法。如果是线性动态数学模型，可采用各种数值解析的算法；如果是非线性动态数学模型可采用神经网络辨识的算法；如果是知识模型可采用基于知识的推理、判断、联想及识别等学习训练的算法，甚至可考虑基于遗传的优化算法。3）智能仿真界面及信息输入的预处理：人机交互界面将朝着多媒体和虚拟现实相结合的方向发展，其智能化表现为具有输入启发、自动识别、判错、报警等功能，使人成为智能仿真系统的一部分。4）仿真结果分析：开发结果分析系统并能给出仿真结果的合理解释乃至从结果知识中发现新知识。

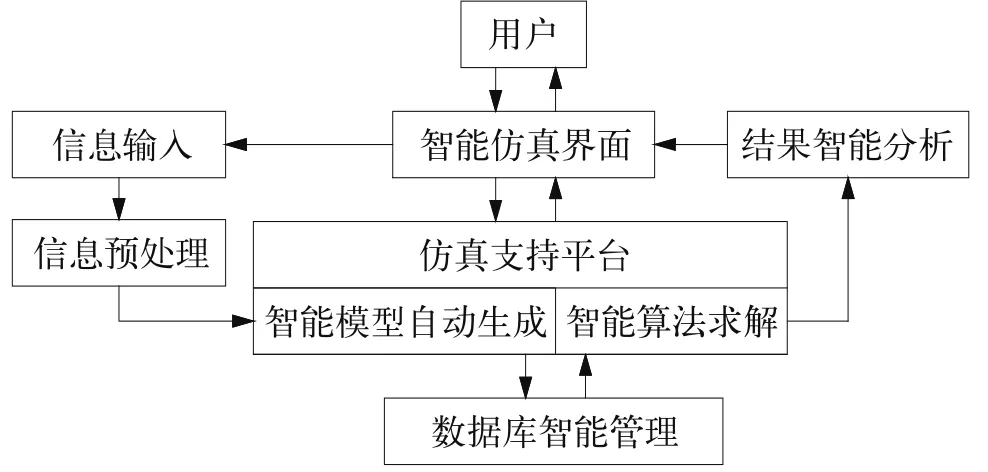
图1 供热智能仿真系统

1.2 供热智能仿真系统功能组成

仿真系统负责模拟供热生产过程，进行预测，提供调度方案，其数据来源依赖于热网监控系统和数据处理系统。在供热智能仿真系统中，系统仿真采用多级模型体系，不仅有快速粗精度实时仿真，还有高精度自学习智能仿真模型，既可以进行静态仿真，还可以进行动态仿真。

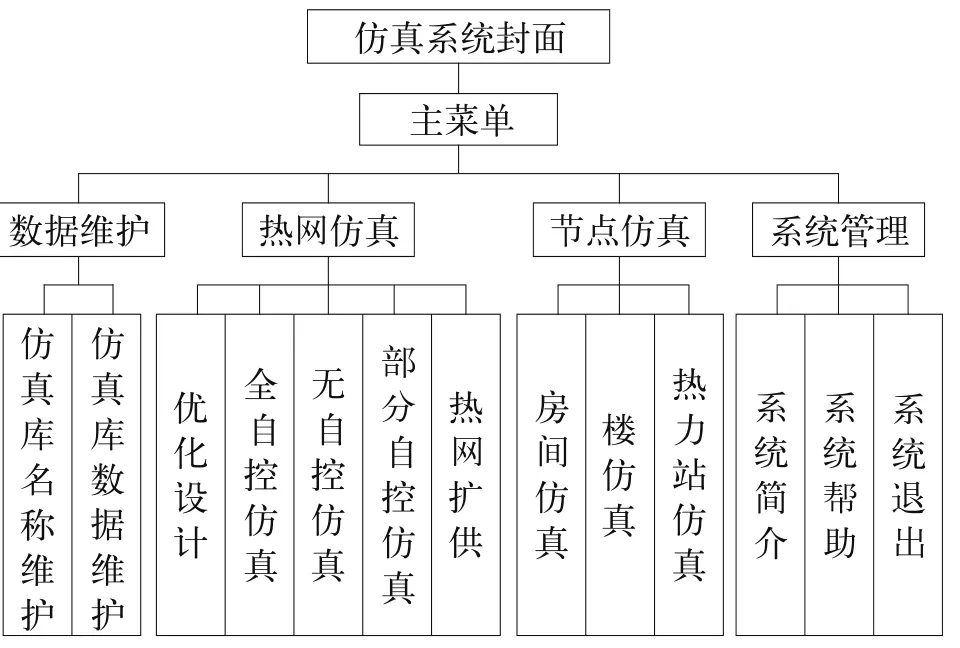
图2 供热仿真系统功能组成

如图2所示，仿真系统中包含系统管理、节点仿真、热网仿真和数据维护等子模块。系统管理主要负责各种对象（节点、管网）数据库的管理（库录入、编辑、查询、插值等功能）；节点仿真是对房间、楼（立管）、热力站这些供热系统中的基本环节建模仿真，研究其动静态特性，为供热优化运行及优化调度提供技术指导；热网仿真是对管道形成的拓扑结果进行分析，参数主要包括流量、压力、管径、阀门开度等，研究全网流量、压力分布场，为热网络运行及热网设计提供理论支持。

2 基于神经网络的供热仿真模型

由于供热系统存在严重滞后，是一个慢时变非线性系统，所以很难用精确数学模型表示对象[3]。神经网络则在求解非线性和不确定性系统方面具有巨大潜力，BP神经网络是非线性系统辨识的有力工具，虽然其辨识速度较慢，但只要采用好的网络结构和算法，就可以用于供热系统环节（房间、楼宇、热力站、热网）乃至整个供热系统的辨识。

2.1 神经网络辨识原理

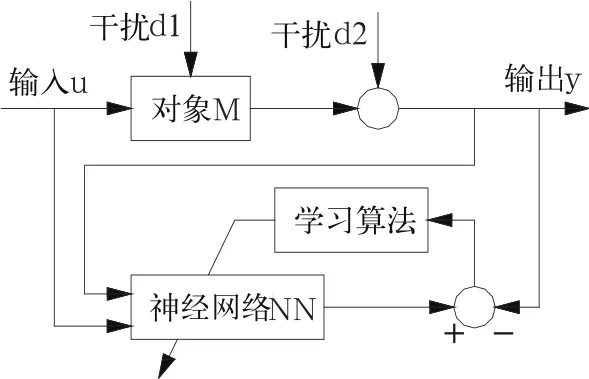
图3 神经网络辨识对象结构图

如图3所示，采用前向建模的串—并神经网络系统辨识结构，即训练一个神经网络用来描述供热系统前向动态特性的过程。将辨识对象的输出经过一个逻辑迟延单元延迟处理之后送入神经网络，与辨识对象的输入组合成一个输入向量，送入辨识网络进行学习，这种结构的学习收敛性和辨识效果较好。当网络训练一段时间后，已逼近对象，则可将网络输出作为网络输入的一部分，从而使网络最终脱离受控对象单独使用，这就是非线性受控对象利用神经网络辨识的思想。这种方法辨识准确，但也存在训练速度慢的缺点[4]。为此，从改进网络结构的角度提出了一种新型快速神经网络辨识的方法。

2.2 快速神经网络模型

由Kolmogorove定理知，任何N变量连续函数可以由单变量连续增函数的线性和非线性叠加而成[5]。这样便可把通常的神经网络结构变成线性和非线性两部分模型结构，用线性系统参数辨识和非线性多层前向网络辨识分别作用于各自对应的结构上，如图4所示。

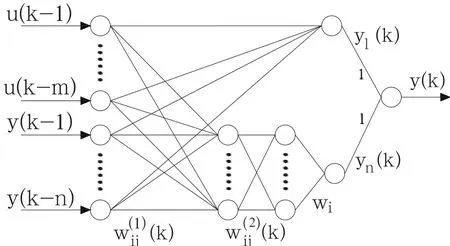
图4 快速神经网络结构模型图

该模型离散化后变为：y(k)=f(y(k-1),y(k-2),…,y(k-n);u(k-1),u(k-2),…,u(k-m))。其中，y(k)为对象输出，u(k)为对象输入，f(.)为非线性函数，wij(1)(k)、wij(2)(k)和wi分别为第1层隐含层、第2层隐含层和输出层的权重。图4中的上半部分输出是线性模型输出yl(k)，下半部分为非线性模型输出yn(k)，由此可得对象输出为：y(k)= yl(k)+ yn(k)。

2.3 快速神经网络算法

根据图4所示的快速神经网络结构模型，对线性结构神经元之间的参数采用递推最小二乘法辨识，对非线性部分神经元之间的权重及阈值采用变学习速率的BP算法的综合辨识方法，网络训练采用两部分模型交替进行，具体算法如下：

1）网络参数初始化，模型中各元素取较小值，权重均匀选取[0,1]随机数。

2）非线性模型权重及阈值不变，对线性模型部分使用递推最小二乘法辨识向量递推N1步后进行下一步。

3）保持线性部分参数不变，对非线性部分采用快速BP算法辨识。调节学习速率的原则是：检查权值的修正值是否降低了误差函数值，如是则说明可对所选取的学习速率增加一个量；否则就应该减小学习速率的值。此方法可以保证网络总是以最大的可接受的学习速率进行训练。自适应学习速率的调整公式如下：

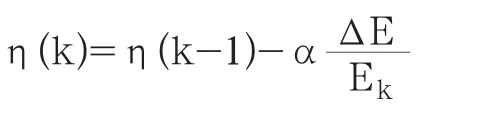
其中，Ek为BP模型中能量指标函数，即输出误差。α为动量项因子，0≤α＜1。

快速神经网络输出层的加权系数wi(k)和阈值θi(k)的调整算式如下：

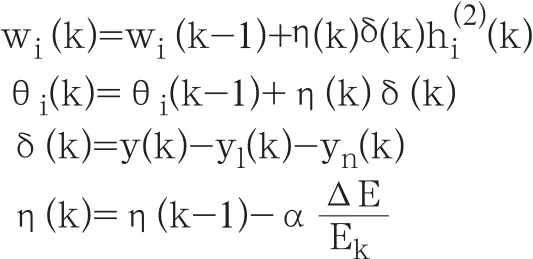
第2隐含层的加权系数wij(2)(k)和阈值θi(2)(k)的调整算式如下：

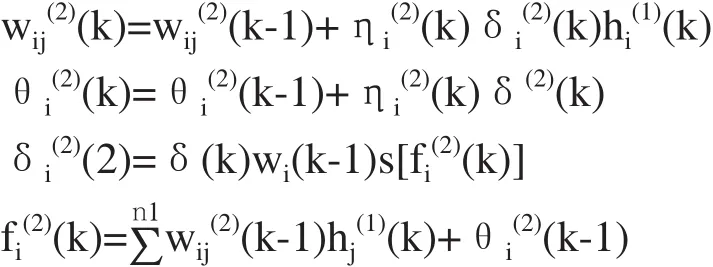
第1隐含层的加权系数wij(1)(k)和阈值θi(1)(k)的调整算式如下：

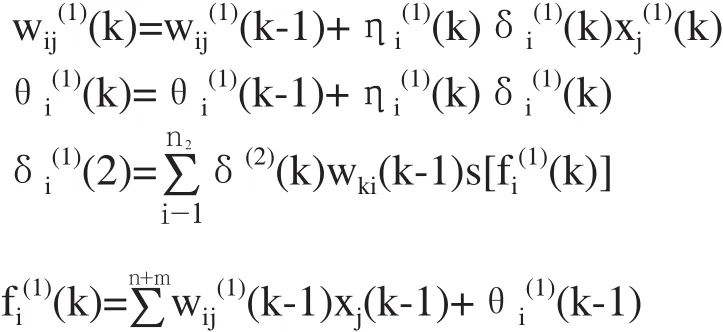
上述算式中，η(k)为学习速率；Ek为BP模型中能量指标函数，即输出误差；s(.)为隐含层神经元激发函数；hi(2)(k)为第2层隐含层神经元的输出；hi

(1)(k)为第1层隐含层神经元的输出。计算网络误差e(k)，若误差未达到指定小正数时，返回到起始步骤，否则结束训练。

2.4 仿真结果分析

2.4.1 非线性对象算例对比分析

取一非线性对象为：

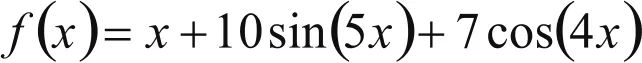
按上述快速神经网络模型结构及变学习速率算法与普通神经网络结构及BP算法分别对该对象进行辨识。采用三层网络：输入层2个神经元；隐层分为两个小层，第一隐层10个，第二隐层5个；输出层1个。选取输入信号x∈[1,5]，按步长0.1递增。从图5和图6的对比中可以看出：在误差精度e(k)=0.01时快速算法训练步数为182，可达到的误差精度为0.00994694；普通算法训练步数为466，可达到的误差精度为0.01023458，从而充分体现出该快速神经网络训练方法具有辨识精度高、训练速度快的特点。

2.4.2 供热系统房间仿真结果

将上述快速神经网络用于对供热系统对象进行辨识，能够保证模型的准确性，同时提高计算速度，为制定供热计划提供有力的依据。以供热系统中标准房间仿真的计算结果为例，在已知室外温度和供水温度的情况下，通过对回水温度和室内温度的实测值与仿真计算值的比较（如表1所示），可以看出快速神经网络模型的仿真效果好，仿真精度高。

3 结束语

基于快速神经网络的辨识方法能够得到更加准确的仿真模型，有效地提高了辨识精度和训练速度，为进一步构建供热智能仿真系统打下了良好的基础，实现了对供热系统这一非线性受控对象进行精确辨识的目的，取得了更好的仿真计算结果。由此可见，智能仿真具备对集中供热系统优化运行和优化设计的指导功能，能够对降低供热运行成本、节约工程投资、提高供热效率起到积极的推动作用。

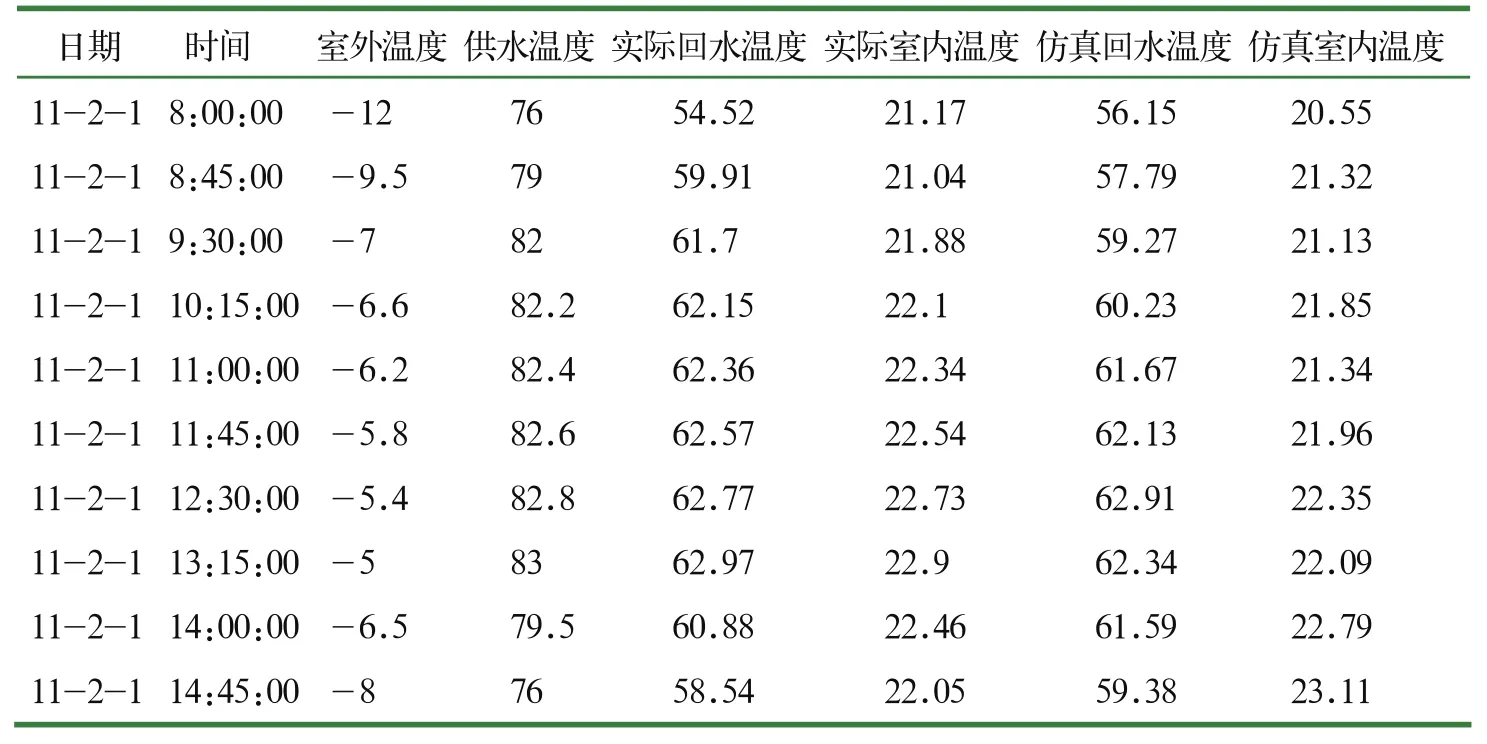
表1 房间仿真计算结果与实测数据对比表

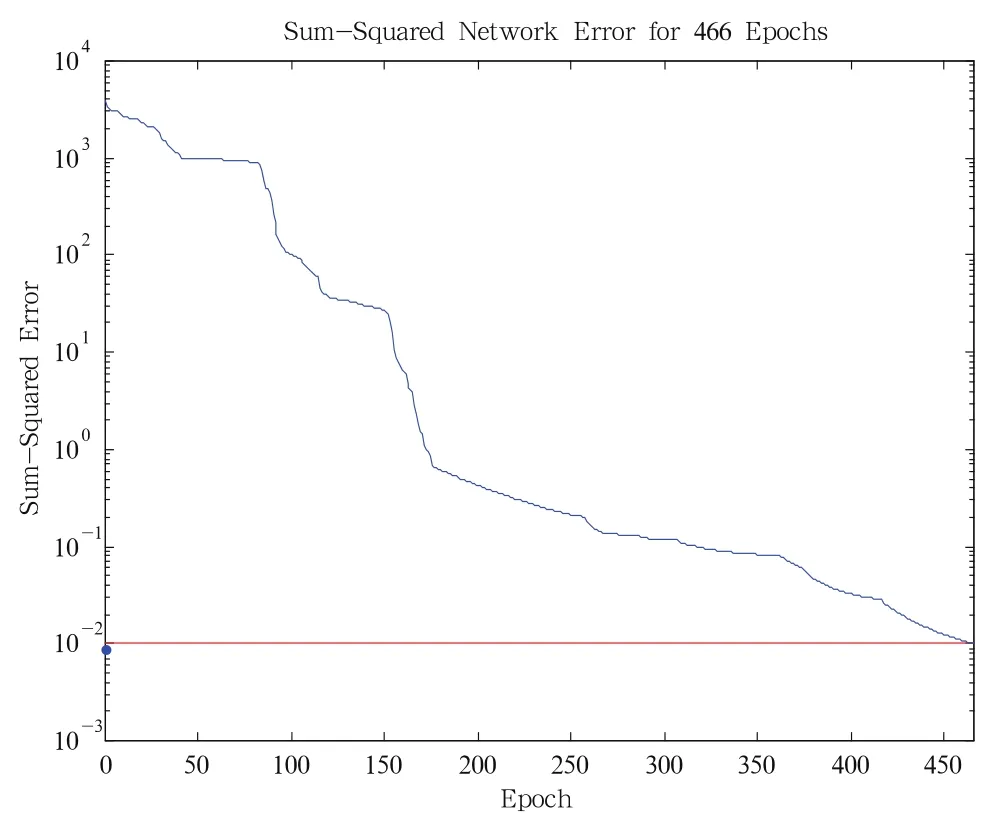
图5 普通神经网络辨识结果误差曲线

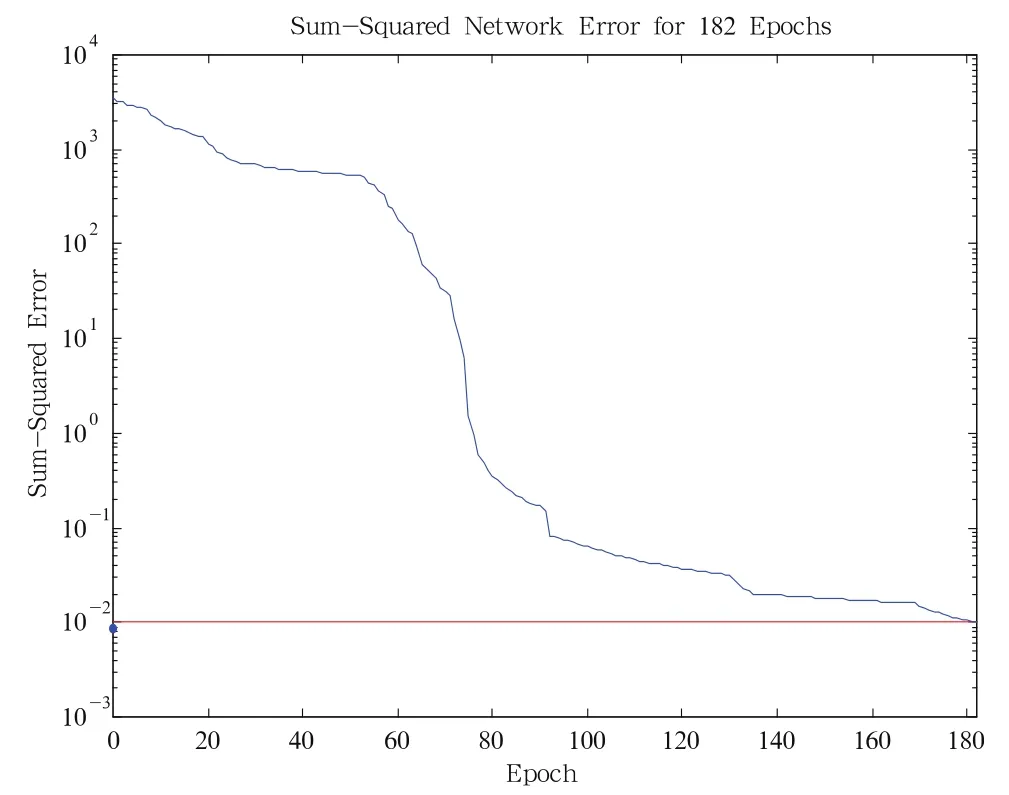
图6 快速神经网络辨识结果误差曲线

[1] 刘贺明.中国城市供热发展与改革情况[J].区域供热,2003,(3):4-8.

[2] 董维敏.集中供热热力站温度控制系统的仿真[J].山西电力,2006(6):32-33.

[3] 李绍勇.广义预测控制在集中供热系统的应用[J].中国建设信息供热制冷,2005(5):81-83.

[4] 朱大奇,史慧.人工神经网络原理及应用[M].北京:科学出版社,2006:36-39.

[5] 滕志东,陈兰荪.高维时滞周期的Kolmogorov型系统的正周期解[J].应用数学学报,1999,(3):446-451.