基于径向基函数神经网络的电动汽车动力电池SOC模型

米 林，赵孟娜，秦甲磊，吴 旋

(重庆理工大学重庆汽车学院，重庆 400054)

由于蓄电池的经济性和技术的成熟性，蓄电池已逐步成为了电动车的主要能源。正如普通车辆必须监视油箱内燃油的容量一样，电动车也需要知道其车载电源能量的大小，而荷电状态(state of charge，SOC)是反映蓄电池能量的重要参数，所以，如何正确获得蓄电池SOC成为电动车应用的重要环节［1－12］。SOC作为蓄电池的内特性，不可能直接进行测量，只能通过对电压、电流、温度等一些直接测量的外特性参数估计［1］。一般主要的估计方法有［2］放电测试法、电解液密度测量法、库仑电量累积法、内阻测量法、开路电压法。以上各种方法虽然各有优缺点，但综合来看，它们的适用场合都有一定的局限性，而本文提出的神经网络测量法则可以克服这一缺点，能够适用于各种工况下动力电池的检测。

1 径向基神经网络的主要原理

1.1 径向基函数神经网络模型分析

径向基函数神经网络(radial basis function Network，RBF)是一种典型的局部逼近网络，是由Moody和 Darken于 20世纪 80年代末提出［12］。它是借鉴生物局部调节和交替接受区域的知识，采用局部接受区域或执行函数的映射关系。与常用的反向传播网络(back propagation，BP)相比，径向基函数神经网络具有更好的逼近能力、收敛性和学习速率［11］。

径向基函数神经网络由3层组成(结构如图1所示)，输入层由一些源点(感知单元)组成，它们将网络与外界环境连接起来，并负责传递输入信号到隐层。隐层节点由像高斯函数那样的辐射状函数构成，隐层的作用是将输入空间到隐空间之间进行非线性变换。在大多数情况下，隐空间具有较高的维数，而输出层节点通常是简单的线性函数。隐层节点中的作用函数对输入信号将在局部产生响应，当输入信号靠近作用函数的中央范围时，隐层节点将产生较大的输出，这种网络具有局部逼近能力，并且径向基函数神经网络的隐空间的维数越高，逼近就越精确。所以径向基函数神经网络的逼近能力、分类能力和学习速度等方面均优于BP网络。这就使得应用径向基函数神经网络来估计电池剩余容量时，得到的估计精度比较高［4，7］。

图1 径向基神经网络结构

径向基函数神经网络的隐层空间起到非线性转换的作用，网络的实现从输入层到隐含层是非线性映射，而从隐含层到输出层是线性映射，总体上看，就相当于一个从高维空间到低维空间的映射。设输入空间为n维，输出空间为m维，则上述映射可表示为H。

1.2 梯度下降的径向基函数神经网络训练算法［7］

当用梯度下降法训练径向基函数神经网络时，需要调整的网络参数有3种:权值、径向基函数中心位置、径向基函数的宽度。在隐层中，每个处理单元的中心位置、扩展参数以及与输出层的连接权值一起经历监督训练过程。先定义瞬时误差函数

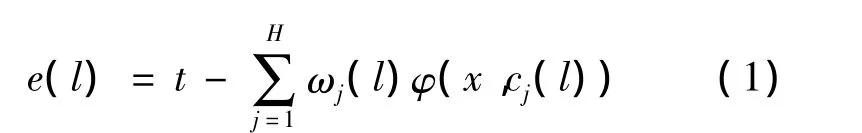
定义目标函数

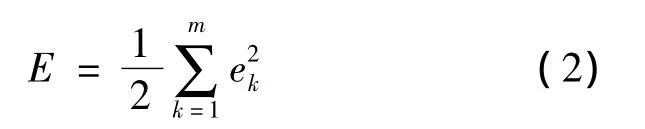
1)输出单元的权值ω更新为

2)隐函数的中心c调整为

3)函数宽度σ调整为

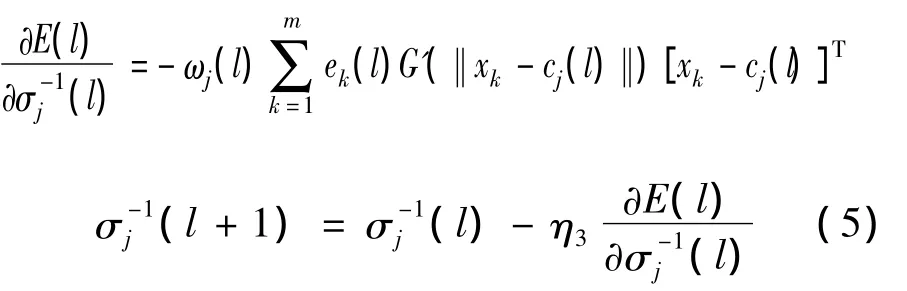
式中η为学习率。

梯度下降的径向基函数神经网络训练算法的步骤:

1)需要从输入向量集中选择足够数量的径向基函数;

3)初始化网络输出层权值为一些小的随机值;

4)提交一个输入向量，并按式(6)计算网络输出，

5)按式(3)～(5)更新网络参数;

6)若网络收敛则停止，否则，l=l+1，转向步骤4)。

具有更新隐层处理单元的中心位置及扩展参数的能力，极大地提高了径向基函数网络的性能，对于给定大小的隐层，与梯度方法一起训练的径向基函数超过一个固定中心的网络。然而，这样增加了训练算法的复杂度，增加了网络的训练时间。

径向基函数神经网络的学习过程分为2个阶段。第1阶段是根据所有的输入样本，决定隐层各节点的高斯函数的中心值和标准化常数;第2阶段是在决定好隐层的参数后，再根据样本信号，同时校正隐层和输出层参数，以进一步提高网络的精度。目前，电动汽车动力电池电荷状态的辨别误差约为8%，正是因为有了径向基函数神经网络，可以使其辨别误差提高到3%左右［8］。

2 动力电池原理及建模分析

2.1 电动汽车动力电池SOC原理分析

目前，国内外较为普遍采用电池的荷电状态SOC［5－6］。作为电池容量状态描述参数，反映电池的剩余容量，其数值定义为电池的剩余容量占电池容量的比值:

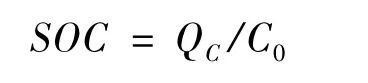
式中:QC是电池的剩余能量;C0是电池以恒定电流I放电所具有的容量。所以 SOC的值一般在0～1。

通常把一定温度下电池充电到不能再吸收能量的状态定义为荷电状态100%(SOC=1)，而将电池再不能放出能量的状态定义为荷电状态0%(SOC=0)。则定义也可表示为

式中Q是电池已放出的电量。

2.2 动力电池的径向基函数神经网络建模分析

由于3层的前向网络具有对任意精度连续函数的逼近能力［9］。本课题采用了3层的径向基函数神经网络。输入层负责传递信号到隐层，隐层采用梯度下降的径向基函数神经网络训练算法，输出层采用纯线性代数来输出信号。

隐层的基函数采用高斯函数，如式(7)所示:

其中:x是n维输入向量;cj是第j个基函数中心，是与x具有相同维数的向量;σj是第j个感知的变量;m是感知单元的个数。

由于神经网络输入变量的选择是否合适，变量数量是否恰当，直接影响模型的准确性和计算量［10］。电池放电过程是一个时变、非线性多变量输入输出并联系统，为的是使神经网络电池模型更好地反应电池的时变特性。模型将电池放电过程中的时变曲线作为神经网络的输入。输入量为3组时间间隔1 s的电池在线端电压V、电池充放电电流I和电池温度θ。输出量为电池的SOC值。

按照式(6)和(7)，通过神经网络预测的电池SOC值为

式中:x为输入向量;ωj是隐层节点到输出节点的权重;cj为高斯函数的中心值;σj为高斯函数的标准化常数。

由于数据的输出在0～1，所以在数据输入时，还要对数据进行归一化处理。如式(9)所示。

其中:X'是归一化以后的值;X是实际的测量值;Xmax和Xmin是实际测量的最大值和最小值。

有了上述理论基础，根据实验的具体条件，选取镍氢电池进行实验(型号为UDDS－US06)。首先对电池的电流、电压、温度等数据进行采集，利用Matlab的newrb函数来创建神经网络，然后根据已有的数据来训练这个神经网络，以提高网络的精度。神经网络训练好以后，再次对数据进行采集，利用采集的数据对SOC进行预测，并与实际测量得到的SOC进行对比，得到实际值与预测值之间的误差，并绘制图形。最后，对整个测试系统添加随机白噪音，再次对数据进行采集，并预测SOC，得到添加噪音以后的数据并绘制图形。

3 实验结果

实验结果见图2～9。

4 结束语

通过对径向基函数神经网络模型预测值与实验所得实际值的比较，可以发现电池SOC估计模型能够利用蓄电池的工作电压、工作电流和表面温度参数估计蓄电池的荷电状态实时值(动态模型)，并且此方法具有较大的抗干扰能力，能够极大地提高电池SOC辨别的精确度，帮助工作人员在实际使用过程中充分发挥动力电池的使用性能。

［1］雷肖，陈清泉.电动车电池SOC估计的径向基函数神经网络方法［J］.电工技术学报，2008，23(5):81－87.

［2］马巍.电动汽车铅酸蓄电池特性建模与荷电状态估计［D］.西安:长安大学，2009.

［3］胡银全.浅析动力电池的充放电及容量检测［J］.中国科技信息，2009(8):142－143.

［4］Cheng H C，Dong D，Zhi Y L，et al.STATE-OF-CHARGE(SOC)ESTIMATION OF HIGH POWER NI-MHRECHARGEABLE BATTERY WITH ARTIFICIAL NEURAL NETWORK［J］.International Conference on Neural Information Processing，2002(2):824 －828.

［5］林成涛，王军平.电动汽车SOC估计方法原理与应用［J］.电池，2004，34(5):376 －378.

［6］胡明辉，秦大同，舒红，等.混合动力汽车电池管理系统SOC的评价［J］.重庆大学学报，2003，26(4):20－23.

［7］史忠植.神经网络［M］.北京:高等教育出版社，2009:140－180.

［8］肖仁耀，肖昕.神经网络在提高锂离子电池检测精度中的研究［J］.测试与测量，2009(9):14－18.

［9］Tsutomu Y，Kazuaki S.Ken Ichiro M1 Estimation of the residual capacity of sealed lead-acid batteries by neural network［C］//Telecommunications Energy Conference，INTEL EC，20th International.［S.l.］:［s.n.］，1998:210－214.

［10］侯媛彬，杜京义，汪梅.神经网络［M］.西安:西安电子科技大学出版社，2007:125－140.

［11］罗玉涛，张保觉，赵克刚.基于神经网络的动力电池组SOC 辨识方法［J］.电源技术，2007，31(11):914－917.

［12］闻新，周路.MATLAB神经网络仿真与应用［M］.北京:科学出版社，2004:285 －299.