两项AVO反演研究及应用

蔡涵鹏 贺振华 李 瑞 黄德济

（油气藏地质及开发工程国家重点实验室（成都理工大学），成都610059）

Zoeppritz方程精确地描述了平面波反射系数与入射角的关系［1］。求解Zoeppritz方程矩阵获得的解析表达式十分复杂，不利于通过解析式分析各参数对反射系数变化的影响，大多数振幅随 炮 检 距 变 化 （amplitude－variation－with－offset，AVO）的研究都是利用两项AVO反演方法实现［2］，例如 国外学 者 Shuey、Smith 和 Gidlow、Fatti等相继提出的两项 AVO近似方程［3－6］，然而这些两项AVO近似式均是Aki－Richards对Zoeppritz方程中P－P波反射系数方程近似的进一步近似。尽管Aki－Richards近似式忽略了非线性的因素，但为了获得新的两项AVO反演方法和进行两项 AVO分析，仍然假设Aki－Richards反演方法能够获得精确的P－P波反射系数。所有的线性两项AVO反演方法推导的基础都是Aki－Richards提出的三项近似式，仅在于约束条件存在差异，因此，所有简化的线性两项AVO反演方法之间存在一定的内在联系。本文从常用两项AVO反演方法的表达式出发，利用解析的方法分析两项AVO近似反演结果与Aki－Richards近似反演结果的关系，证实两项AVO反演结果相互转化的可行性，分析推导新的两项AVO方法的可能性，阐述提高两项AVO反演精确度的校正方法，分析新方法在实际地震数据AVO分析的应用效果。

1 常用两项AVO近似式

假设地下有一反射界面，界面上层介质和下层介质的密度和纵波、横波速度分别为和则 Aki－Richards近似式［7］为

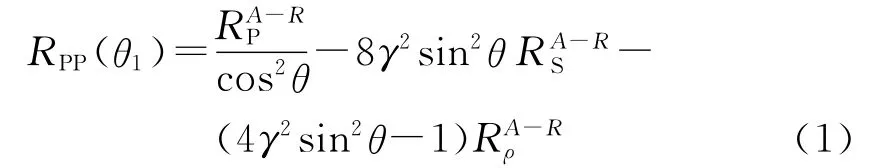
式中：θ1为入射角；RPP为纵波激发纵波接收时的反射界面的反射系数；θ为入射角和透射角的平均值为纵波速度变化率为横波速度变化率为反射界面两侧密度变化率为横波与纵波速度比，γ＝

在实际研究中，三参数的Aki－Richards近似式通常都被数值不稳定性困扰，减少参数的维数可使得反演结果更加稳健，因此，Aki－Richards近似式被一系列的两项近似式进一步简化。

Shuey（1985）利用曲线拟合法，拟合反射波振幅随入射角度变化的曲线，获得截距（A）和梯度（G ）的信息［3］，表达式如下

（2）式适用于入射角度在0°～30°范围内进行AVO分析，即仅仅适用于小入射角度的AVO分析。

Smith和 Gidlow［5］（1987）利用速度与密度的关系（Gardner关系式）［8］，使用RP替代Rρ估算RP和RS，获得表达式

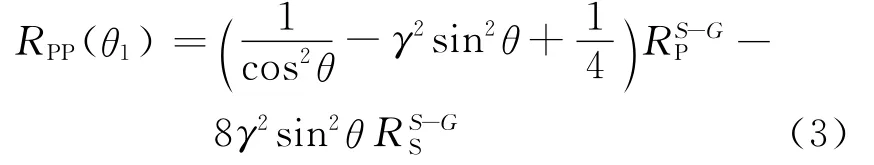
此近似式虽然对角度的范围没有限制，但是速度与密度必须满足经典Gardner关系的条件，否则估算的结果误差较大。

Fatti等（1994）根据与估计的参数纵波阻抗变化率（RI）和横波阻抗变化率（RJ）相比，反射界面两侧密度变化率（Rρ）的影响可以忽略不计的假设，获得表达式［6］

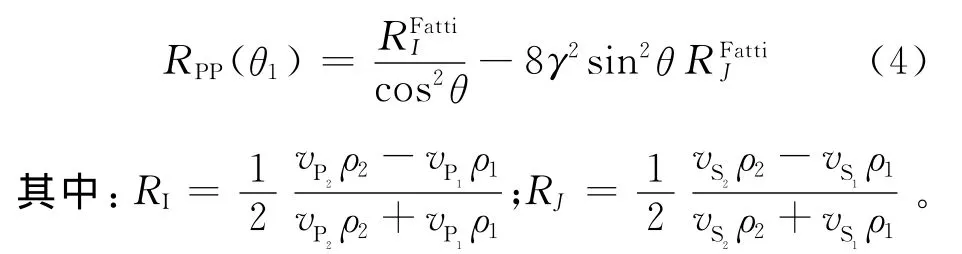
（4）式的推导假设了密度变化率的影响可以忽略，密度的信息主要蕴含在大角度的道集中，因此（4）式与（2）式一样，不宜用于大角度的AVO分析。

在不同的假设前提下，简化的两项AVO近似式估算出了参数的不同近似值；但是，由于他们简化的基础公式都是Aki－Richards近似式，最基本的信息来源都是相同的。因此，根据假设前提，利用约束条件推导适当的公式使得不同近似式估算参数能够实现互相转换。

2 等效性分析及新方法

理解各种两参数AVO反演方法的内在联系，有助于改进两参数反演方法。由于两参数AVO反演仅仅包含2个未知数，利用2个角度（θ＝0和θ＝θmax）处的反射地震数据能够解析完成相应的两项AVO参数反演［9］，也就是意味着在θ＝0和θ＝θmax处，利用两项AVO获得反射系数和三项Aki－Richards表达式获得反射系数值相等，例如对于Smith－Gidlow方法，在给定的2个角度处，有如下的关系式成立

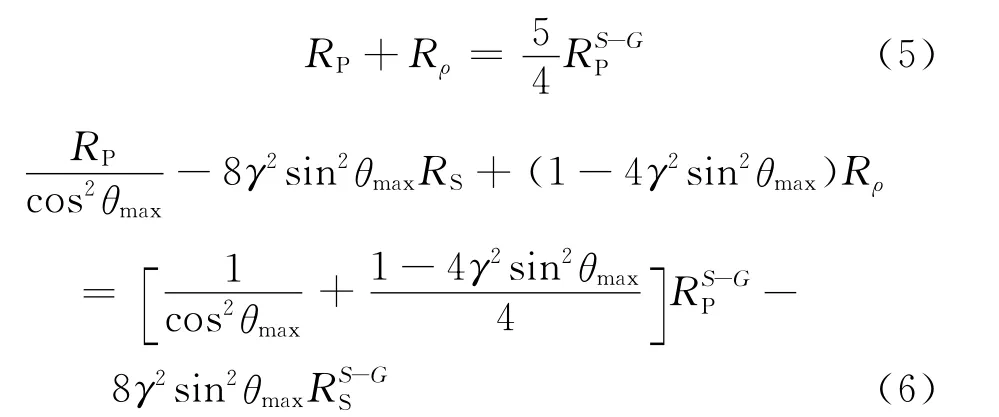
（5）式和（6）式中没有上标的RP、RS和Rρ为利用三参数Aki－Richards近似式估算的结果。以下所有公式中，没有上标的参数均为三参数Aki－Richards近似式估算的结果。

联立求解方程式（5）和（6），得到

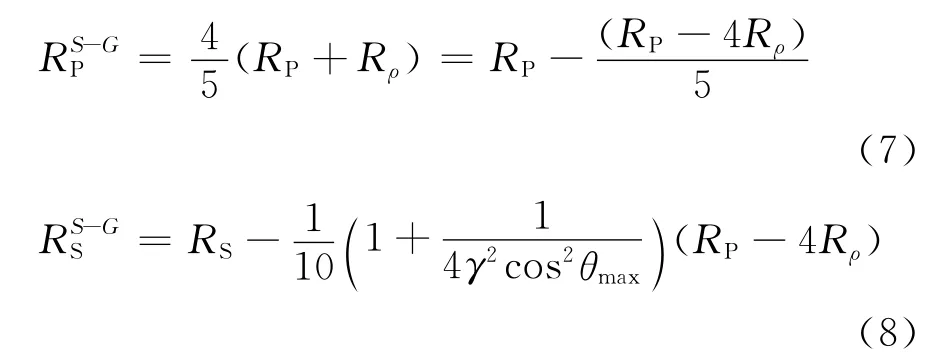
（7）和（8）式中均包含有RP－4Rρ，即当反射界面两侧的纵波速度变化率等于其密度的变化率的4倍时，应用Smith－Gidlow近似方法反演结果与Aki－Richards三参数近似式反演结果是一致的。

同理可获得，其他近似式反演结果与Aki－Richards三参数近似式反演结果的关系。

对于Fatti近似式有

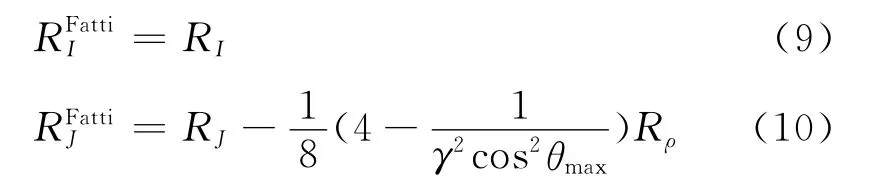
（9）式表明，利用Fatti近似式可以获得与Aki－Richards三参数近似式反演一致的纵波反射率。误差表达式（10）表明，在γ确定时，选择合适的最大角度（最大角度小于临界反射角度）可以减少利用Fatti近似式估算横波变化率的误差，从而提高估算的RFattiJ的精确度。

对于Shuey近似式有

（11）式表明利用Shuey近似式计算的截距其物理含义为纵波反射率，且与Aki－Richards三参数近似式估算的纵波反射率一致。（12）式表明应用Shuey近似式获得梯度信息中包含纵波反射率、横波反射率和密度变化率的信息。（12）式等号右边的第3项与（10）式等号右边的第2项具有相同的物理含义及作用。

（7）～（12）式表明，用于AVO反演的γ值和θmax在给定或者估计出的情况下，两项AVO反演结果都与Aki－Richards三项近似结果有直接的关系，能够相互转换。值得注意的是，（7）～（12）式仅仅对于应用2个炮检距数据进行参数反演是精确的成立，然而通常在实际资料的情况中，为了压制噪声干扰，需要利用多个炮检距的地震道集。从（8）、（10）和（12）误差表达式可以发现，在常用的两项AVO近似式估算参数结果基础上，通过局部的校正可以获得更加精确的参数估计，通过修正误差表达式可以获得用于AVO分析新的两项AVO近似式。

Fatti近似在近炮检距范围内与Aki－Richards近似较接近，而Smith－Gidlow近似在远偏移距（接近临界角）范围与Aki－Richards近似较接近。近炮检距反射系数主要受纵波速度变化率控制，中等角度主要受横波速度变化率控制，因此，综合提高横波反射率精确度的方法和利用Rρ≈RI／5（Gardner关系式），以及 Fatti近似和Smith－Gidlow近似的优点，推导出与方程式（3）和（4）类似的新的两项AVO表达式［10］

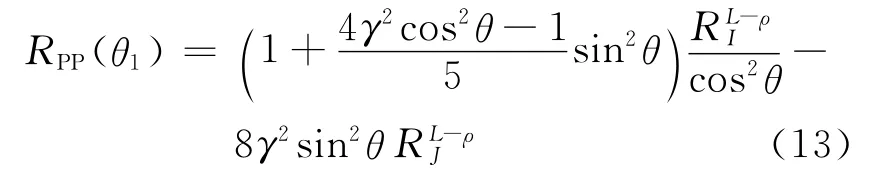
应用前面提到的两点解析法可以得到

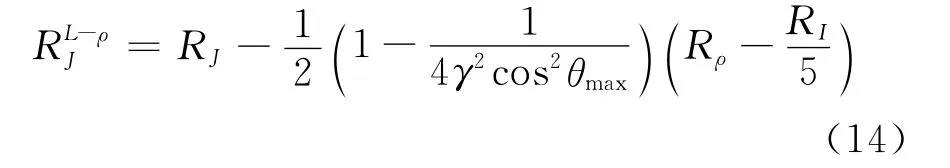
（14）式表明，RJ估算的误差项中包含了Fatti近似和Smith－Gidlow近似中减小RJ估算的相应项。选取较大的入射角度（小于临界反射角度），或者修正纵波反射率与速度变换率的关系，能够提高RJ估算精确度。RJ精确的估算是非常重要的，例如在流体识别、岩性识别中的应用，在获得AVO属性上，进一步进行波阻抗反演处理等［11］。更重要的是，（14）式清晰地显示该近似式在密度变化率较大的情况下非常有用，例如，当用Rρ代替Rρ－RI／5时，即反射界面两侧纵波反射率等于反射界面两侧密度的变化率的5倍，（14）式与（10）式等价，此时代表最大的密度变化率，因此称（13）和（14）式中上标L－ρ为适应于密度较大变化率情况近似方法的标记。

根据含气砂岩的分类，设计4个上覆岩性为泥岩和下伏岩性为含气砂岩的2层单一界面模型，4个模型的弹性参数见表1，模型的弹性参数来自于参考文献［12，13］。4种含气砂岩的模型中，页岩和含气砂岩的密度差异都较大。对于不同种类的含气砂岩模型，利用不同的两项AVO近似式计算的反射系数结果对比见图1。图1的结果证实，即使在上覆页岩与含气砂岩密度差异较大的情况下，无论是在近角度（近偏移距）还是远角度（远偏移距，但小于临界角反射偏移距），新的近似式计算的反射系数较其他几种近似式计算的反射系数与Aki－Richards提出的三项AVO近似计算的反射系数更接近；即模型分析证实，在入射角小于临界角的前提下，结合Fatti近似和Smith－Gidlow近似优点的近似式既适合于小偏移距的AVO分析，也满足大偏移距AVO分析的需求，因此称（13）式为全偏移距近似式（full－offset approximation）。

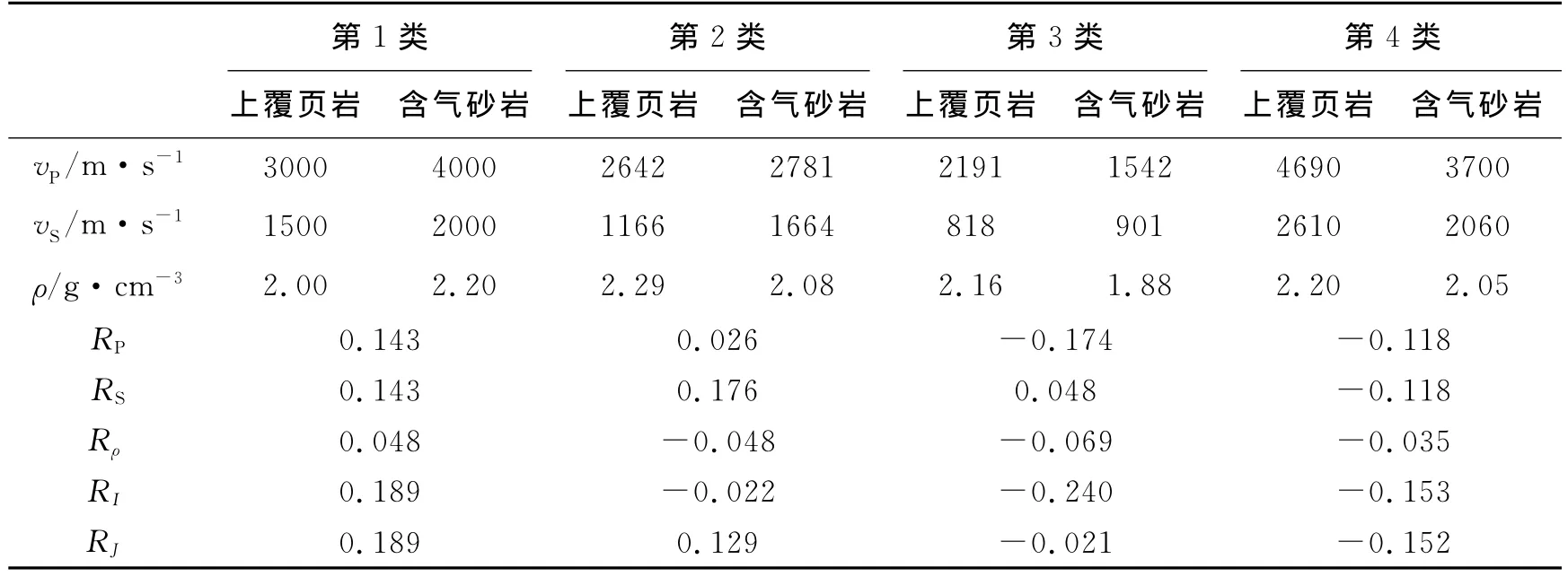
表1 4类含气砂岩与页岩模型弹性参数Elastic parameters of four types of gas sand and shale models

由于全偏移距近似式包含有Smith－Gidlow近似式中使用的Gardner关系式假设，即速度与密度具有正相关的性质。然而在设计的第2类含气砂岩模型中，反射界面上下岩性的纵波速度与密度的关系不满足Gardner关系式，密度变化率绝对值约等于纵波速度变化率的2倍，并且密度的变化率主要影响大角度的反射系数；因此，应用全偏移距近似式计算的结果在入射角度超过30°后，与Aki－Richards提出的三项AVO近似结果具有较大的误差。在设计的第1、第3和第4类含气砂岩模型中，纵波速度变化率约等于密度变化率的3倍，与经典的Gardner关系式接近，即密度变化率与纵波速度变化率的关系直接影响着全偏移距近似结果与 Aki－Richards提出的三项AVO近似结果的相似程度。因此，对于ΔvP／vP≠4Δρ／ρ（Δ表示梯度或者微分计算）的情况，尤其是与Gardner关系式相差甚远的情况时，对估算参数进行校正是有必要的。

3 局部校正方法

虽然全偏移距近似式能较好地适应大角度的AVO分析，但是该近似与Smith－Gidlow近似具有同样的前提假设，包含经典的Gardner提出的速度与密度的关系，因此应用Gardner关系式可以局部地校正估算参数的结果。根据Gardner关系通用形式ρ＝αv1／βP（α和β为实系数，由声波和密度测井曲线分析获得），和微分性质得到

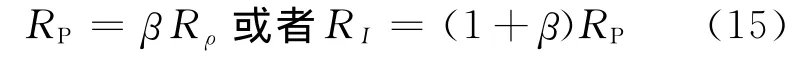
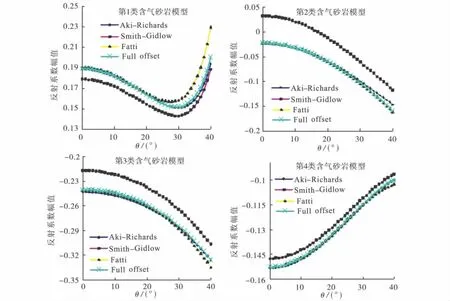
图1 不同近似式计算的反射系数对比Fig.1 Comparison of the calculated reflection coefficients from different approximate formulas

（7）、（8）和（14）式是β＝4的典型情况。由（15）的关系式，将（7）、（8）和（14）式分别改写成包含β为变量的表达形式

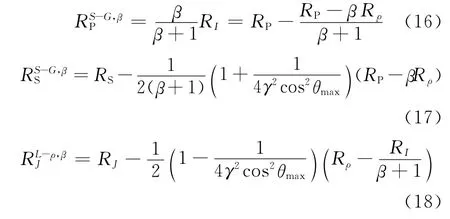
为了将β＝4估算的结果转化为β≠4的估计结果，需要对（7）、（8）和（14）估算参数进行校正。（16）式除以（7）式消除RI，获得基于Smith－Godlow近似式估算的纵波速度变化率参数校正表达式

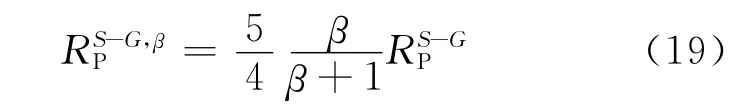
（17）式与（8）式相减消除RJ，获得 Smith－Godlow近似式估算横波速度变化率结果校正表达式

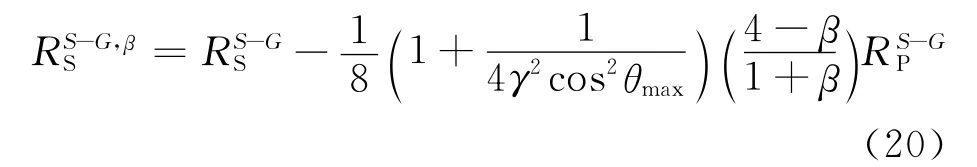
同理，（18）式与（14）式相减消除RJ，整理获得基于全偏移距近似式估算的横波反射率校正表达式

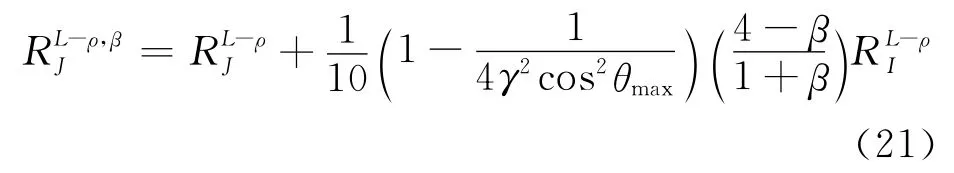
（19）、（20）和（21）这3个表达式就允许利用Gardner关系对AVO反演获得的参数进行合理修正。由于以上各个校正表达式的推导均建在速度与密度满足Gardner关系式的基础上，Gardner关系式适用于砂泥岩地层，故利用（19）、（20）和（21）式可以完成砂泥岩地层AVO分析结果的校正。值得注意的是Gardner关系式隐含着速度与密度成正相关的关系，因此，在应用以上校正表达式时，应该首先通过测井或者岩石物理资料分析速度与密度的关系，否则可能获得与期望相反的结果。例如岩石物理测试分析证实裂缝性的碳酸盐岩地层速度与密度可能成负相关，而孔隙性的碳酸盐地层速度与密度的关系与Gardner关系式有着较好的对应［14］。

4 实例分析

实例分析数据来自于Hampson Russell软件AVO模块的测试数据。图2为2个原始共中心点角度道集（common middle point），在1.33s附近具有明显的AVO异常信息特征。图3为该地区1口钻井纵波速度与密度的交汇图。根据Gardner关系式的形式获得密度与纵波速度的关系为：ρ＝0.4855×，即进行局部较正时，校正公式中β＝5.13。图4为原始角度道集叠加剖面。常规叠加剖面中仅仅能识别位于1.33s附近的穹窿构造特征信息，其他地质特征信息（如断层、1.46s附近叠瓦状沉积）难以识别。

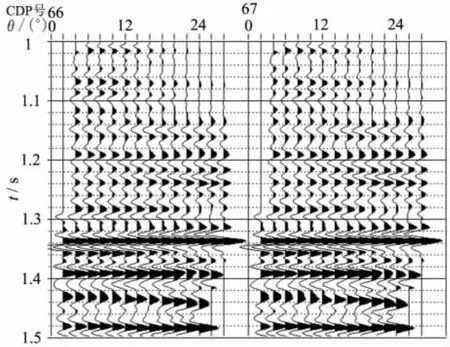
图2 原始角度道集Fig.2 Original angle gather

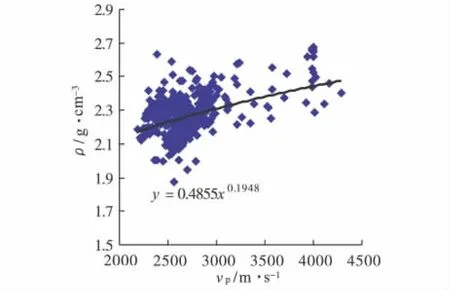
图3 纵波速度与密度的交汇图Fig.3 Compressional velocity versus density

加权叠加技术在AVO反演中占有一定的位置。AVO反演中的加权叠加就是根据做完动校正后的共中心点道集上出现的AVO信息估算反射界面两侧地层参数相对变化率（RP、RS、Rρ、RI、RJ等）的定性分析方法，具有计算速度快、不受其他方法（如非线性反演）中遇到的多个局部极小的困扰、不需要知道实际子波等优点，因此，本文计算纵波阻抗反射率和横波阻抗反射率采用加权叠加技术。由于全偏移距两项AVO近似较其他两项AVO近似公式更加适合于更大的角度（不超过临界角度），采用公式（13）计算加权系数。利用加权叠加技术获得的纵波阻抗反射率和横波阻抗反射率剖面见图5和图6。纵波阻抗反射率和横波阻抗反射率剖面分别相当于纵波和横波的零炮检距叠加剖面。比较图5和图4，可以发现估算的纵波阻抗反射率剖面比动校正后的CMP叠加剖面具有更高的分辨率、更多的地质特征结构信息（如断层、叠瓦状构造，图4中箭头处）。

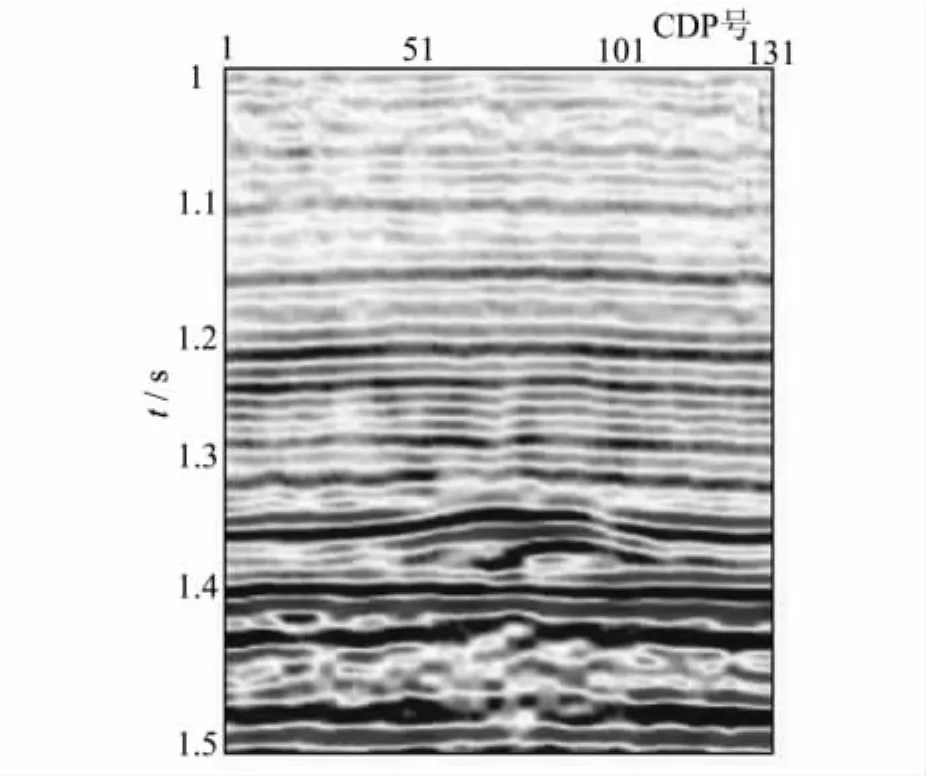
图4 原始角度道集叠加剖面Fig.4 Stack section from original angle gather

图5 纵波阻抗反射率剖面Fig.5 Reflectivity of P impedance

图6 横波阻抗反射率剖面Fig.6 Reflectivity of S impedance

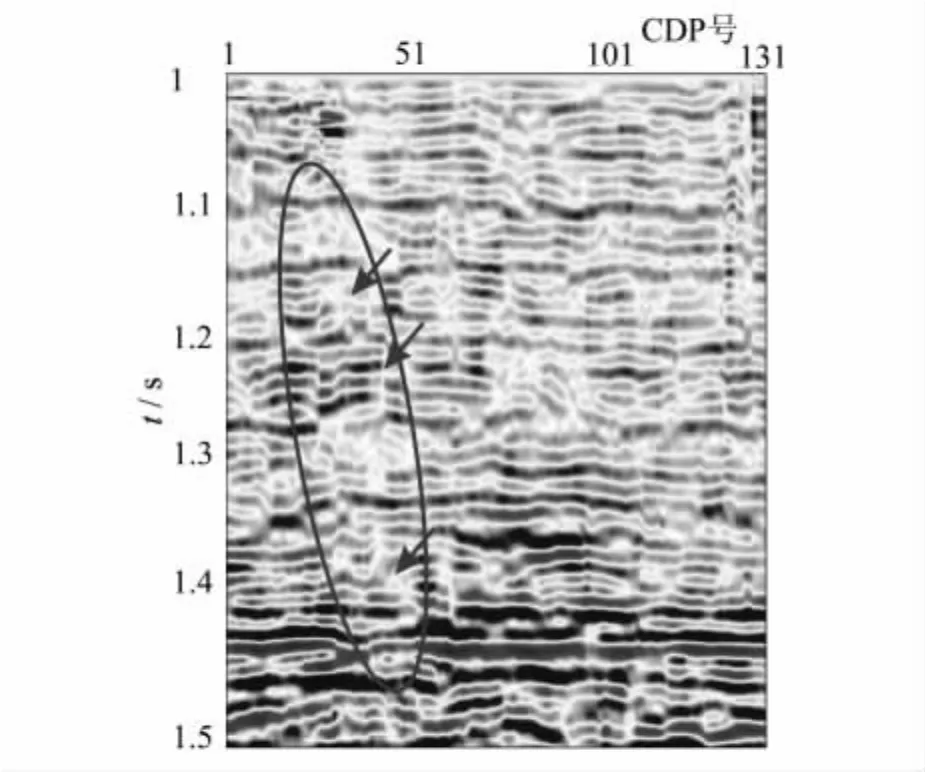
图7 校正后的横波阻抗反射率剖面Fig.7 Reflectivity of S impedance after calibration

图7为图6中横波阻抗反射率剖面利用公式（20）校正后的横波阻抗反射率剖面。在图7中，断层成像较图6中的成像清晰（如图7中黑色虚线椭圆内箭头标注处）。因此，通过合适的局部校正方法可以改善反射率剖面的成像质量，提高解释的准确性，也证实了局部校正的重要性。

5 结论与认识

两项AVO反演方法具有等效的信息成分，不意味着所有两项AVO方法均给出相同的反演结果，而是在入射角度小于临界角的条件下，应用合适的转化公式，可以实现不同方法反演结果之间互相转换。利用不同两项AVO近似式与Aki－Richards近似式之间的误差表达式导出的、结合经典Fatti和Simth－Gidlow近似方法优点的全偏移距两项AVO近似方法，可以更加精确地估算横波阻抗反射率，特别适合于反射界面两侧密度具有较大变化率情况。此外，对于隐含有Gardner关系式的两项AVO反演结果，应用局部校正方法前应该首先分析地层密度与速度的关系，确定是否应该通过局部校正来改善地质结构的成像质量，提高解释的精度。

［1］Zoeppritz K，Erdbebenwellen VIIIB.On the reflection and propagation of seismic waves［J］.Gottinger Naehriehten，1919，1：66－8.

［2］Charles P U，Robert R S.Two－term AVO inversion：Equivalences and new methods［J］.Geophysics，2008，73（6）：C31－C38.

［3］Shuey R T.A simplification of the Zoeppritz equations［J］.Geophysics，1985，50（4）：609－614.

［4］Castagna J P，Swan H W，Foster D J.Framework for AVO gradient and intercept interpretation［J］.Geophysics，1998，63（3）：948－956.

［5］Smith G C，Gidlow P M.Weighted stacking for rock property estimation and detection of gas［J］.Geophysics Prospect，1987，35（9）：993－1014.

［6］Fatti J L，Strauss P J，Stallbom K.A 3－D seismic survey over the offshore F－A gas field［J］.South Af－rica Geophysics Rev，1994，1：1－22.

［7］Aki K I，Richards P G.Quantitative seismology［M］.San Francisco：W H Freeman and Co，1980：135－137.

［8］Gardner G H F，Gardner L W，Gregory A R.Formation velocity and density－The diagnostic basis for stratigraphic traps［J］.Geophysics，1974，39（6）：777－780.

［9］Ursenbach C.Two new approximations for AVO inversion：national convention［C］／／Canadian Society of Exploration Geophysicists， Expanded Abstracts，2004：SO31.

［10］Ursenbach C，Stewart R R.Extending AVO Inversion Techniques：CREWES Research Report 13［R］.Calgary：University of Calgary，2001.

［11］宋宗平.应用AVO属性数据进行波阻抗反演处理［J］.石油地球物理勘探，2004，39（4）：465－467.

［12］Fred J H.地震振幅解释［M］.北京：石油工业出版社，2006：56－57.

［13］Castagna J P，Smith S W.Comparison of AVO indicators：a modeling study［J］.Geophysics，1994，59（12）：1849－1853.

［14］Agersborg R.Seismic properties of carbonate rocks with emphasis on effects of the pore structure［D］.Bergen：University of Bergen，2007.