对数能量熵的最优小波包基搜寻算法

李姣军，唐 娜，苏理云，徐 勤

(重庆理工大学 a.电子信息与自动化学院;b.数学与统计学院，重庆 400054)

近年来，小波包得到了快速发展，被越来越多地应用到通信及其他领域中［1－8］。由于小波包有多种分解结构，其中会有一种分解结构可以最好地表达被分析的原始信号，这种分解结构就是最优的小波包基，所以很多人把研究方向投入到最优小波包基的搜寻算法。目前所使用的最优小波包基选取算法大致可归为2类:一类是Volkan Kumbasar等［9－10］所提出的 Brute Force Algorithm(BFA)算法;另一类是1992年 Wickerhauser与Coifman［11－12］提出的基于熵值的 Best Basis Selection(BBS)算法。BFA算法的基本过程是列举所有可能的二叉树结构，对其中满足完全重构条件的二叉树结构进行对比，选取其中度量函数最小的一组结构作为最优基。BBS算法则是采用对完整小波包二叉树结构进行自下而上的“静态修剪”方法选择最优基，算法简单且高效［13］。BFA算法适用性要优于BBS算法，但计算复杂度高于BBS，实用性不强。本文在BBS基础上，选择对数能量函数作为熵，进行最优小波包基的搜寻。

1 小波包介绍

小波包变换是小波变换的延伸，小波变换仅对信号的低频部分进行分解，而小波包变换则是对信号进行低频分解的同时也要对高频部分进行分解。因此与小波变换相比，小波包变换为信号频带分析提供一种更精确的方法。对比小波分解，小波包分解的优势主要表现在3个方面［14］:

1)可以对频带进行多层次划分;

2)小波包不仅对轮廓(低频)进行分解，还对多分辨分析没有细分的细节(高频)部分进行进一步的分解;

3)自适应选择频带，使其与信号频谱相互匹配，提高了时频分辨率。

由于小波包较小波体现了更多的优势，因此，目前对小波变换的研究和应用较为广泛。小波包的定义:

由

所定义的函数 φn(n=2l或2l+1，l=0，1，…)为关于正交尺度函数Φ(t)的小波包。这里:φ0(t)=Φ(t)称为尺度函数;φ1(t)=φ(t)称为为小波函数;h0k和h1k分别为尺度函数和小波函数对应的低通滤波器系数。

小波包有多种形式的分解，不同的小波包分解结构具有不同的性质，且反映不同的信号特征。众多的分解结构构成小波包基库，每一种小波包基都能够完整地保存信号的全部能量，并可以对原始信号进行重构，因此在对待分析信号进行小波包分解时，希望根据不同的信号特征在小波包基库中选择一个最好的小波包基来表达信号的特点。对信号f(t)进行小波包分解时，是将信号投影到小波包基上，从而获得一系列系数，并用这一系列的系数来刻画f(t)的特征。如果这一系列系数之间值的差距越大并且只有少数系数很大，则越好，因为可以用这些少数大的系数代表f(t)的特征，显然这样的小波包基则是所要寻找的较优的基;但如果这一系列系数值的差别并不大，也就是刻画信号的系数携带的信息差不多，则能量集中性差，会使权重接近而难以取舍，那么很难找出f(t)的特征，因此与之对应的基就不是最优基。下面提出一种最优小波包基的搜索算法，并应用到多载波通信系统中。

2 最优基算法

2.1 最优基的选择

从小波包基库中任意选取1个小波包基均能在不同程度上反映待分析信号的特性，只是每个小波包基反映信号所用的数据量不同，最优小波包基应该是用尽可能少的数据来反映尽可能多的信息。对某一特定信号而言，选择一个“最优度量准则”下性质好的最优基进行分解，则可以使展开的系数之间存在明显差异，这样便可以较好地刻画信号特征。对于如何选择最优基，通常是要定义一个信息花费代价函数，对于一个给定的向量来说，代价越小表示越有效。然后在小波包库中寻找一个使代价函数最小的基，那么此基便是最优基。其中最关键部分就是信息花费代价函数。代价函数的定义有很多种，选取原则也较为宽泛，任何关于序列的实函数、能测得集中度的可加性函数均可作为代价函数。通常作为最优小波包基搜索的代价函数有门阀函数和熵，其中以熵应用最为普遍，且大部分的文献是应用香农(shannon)熵。但是熵也包括很多种类，比如 lp范数熵、SURE熵、对数能量熵等，而本文则选用对数能量熵作为代价函数，打破一直以来应用shannon的惯例。对数能量熵的定义为［15］

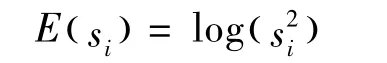
其中:s是待分析原始信号;si是在正交基上的投影系数，同时满足E(0 )=0，且，即熵E是递增的价值函数。熵值直接反映了它所处状态的均匀程度:熵值越小，它所处的状态越是有序，越不均匀;系统的熵值越大，它所处的状态越是无序，越均匀。本研究希望用小波包对待分析信号分解时的系数之间的差异明显，即不均匀性，这样易舍弃非关键信息，用较少数的数据反映尽可能多的信息。最优基的选择能使分解系数间彼此有较大差异而信息损失又较少。

2.2 最优基的快速搜索

假设小波包树是一个N层分解的二叉树，则整个搜索过程是对小波包二叉树结构进行由下而上的“静态修剪”，计算每个节点处的信息花费代价函数即对数能量熵，并从底层开始逐级向上比较父节点与子节点的信息花费代价函数的大小。若父节点比子节点之和的对数能量熵小，则保留父节点的对数能量熵值，否则以子节点之和的对数能量熵值代替父节点，然后再同更上一层进行上述比较，直至搜索到最顶层，此时的树结构便是最优树结构，即最优小波包基［16］。整个搜索过程如图1所示。

2.3 算法实现举例

应用Matlab按照上述搜索方法对输入的语音信号test进行小波包分解，搜索最优小波包基。此处以N=3为例。

图2中各节点处所标注的数字为各节点的对数能量熵值，即代价函数，如图2(a)所示;然后自下向上搜索，计算末端节点熵值，与上一层父节点比较，标记熵值最小的节点，如图2(b)所示;最后按照标记的输出，得到最优基。

图1 最优小波包基搜索流程

图2 最优小波包基搜索例图

2.4 算法应用

近几年，在通信领域中小波包的应用非常广泛，尤其是在多载波调制系统中。由于小波包自身具有良好的尺度正交性和平移正交性，可以作为多载波调制系统中的子载波，来对抗子载波间干扰和符号间干扰。这种调制方式称为基于小波包变换的正交多载波调制，简称小波包调制。这种调制方式有多种方案［17］，其中以小波包分复用(wavelet packet division multiplexing，WPDM)技术最为突出。WPDM主要是将一串数据流经串并变换后转换成K路子数据，每一路子数据用小波包函数进行调制。由于WPDM中应用小波包函数调制子数据流，那么就涉及到最优小波包基的选择，将本文所讲述的算法应用到WPDM中，把搜索得到的最优小波包基根据子载波分配算法分配给各子数据流进行调制，这样可以有效地提高频谱利用率、实现频带利用最优化，提高数据传输速率，进一步提高通信系统性能。

3 结束语

本算法是在已成熟的BBS算法基础上进行创新，以对数能量熵代替香农熵进行最优小波包基的搜寻，算法简单高效，实用性强，但仍具有一定的缺陷(如在未知分解层数即未知末端节点的情况下算法受到约束)，有待进一步改进和提高。本算法的一个应用领域是多载波通信系统，但对于应用小波包进行图形处理、故障诊断等诸多领域同样适用。

［1］龚仁喜，宁存岱，谢井华，等.基于LabVIEW和小波分析的电力电缆故障定位方法［J］.重庆理工大学学报:自然科学版，2010，24(1):65 －70.

［2］胡坤，徐亦凡，何斌.改进小波变换方法在鱼雷控制系统中的应用［J］.四川兵工学报，2010，31(2):32－34.

［3］汪小梅，朱华.一种改进的小波变换阈值去噪法［J］.重庆理工大学学报:自然科学版，2010，24(6):48－51.

［4］晏力.基于小波变换的自参照图像数字水印研究［J］.重庆工商大学学报:自然科学版，2010，27(1):50－54.

［5］董湘君.基于局部协方差模型的小波图像降噪［J］.激光杂志，2010，31(3):22 －23.

［6］张志红，任杰.B样条小波边缘检测改进算法［J］.四川兵工学报，2010，31(2):136 －138.

［7］晏力.基于小波变换的数字图像压缩研究［J］.重庆工商大学学报:自然科学版，2009，26(4):341 －345.

［8］范永辉，王刚，曲文娟.基于小波域分类隐马尔可夫树模型的图像融合算法研究［J］.激光杂志，2009，30(5):32－34.

［9］Volkan Kumbasar，Oguz Kucur.Better wavelet packet tree structures for PAPR reduction in WOFDM systems［J］.Digital Signal Processing，2008，18:885 －891.

［10］Volkan Kumbasar，Oguz Kucur.Better wavelet packet tree based OFDM for multipath powerline channel［J］.Computers and Electrical Engineering，2010，36:397－403.

［11］Laksmanan MK，Nikookar H.Review of wavelets for digital wireless communication［J］.Wireless Personal Communications，2006，37:387 －420.

［12］Yang Jingyu，Xu Wenli，Dai Qionghai.Fast adaptive wavelet packets using interscale embedding of decomposition structures［J］.Pattern Recognition Letters，2010，31:1481－1486.

［13］李姣军.一种快速自适应最优小波包基搜索算法［J］.现代电子技术，2011，34(11):72 －75.

［14］ZHONG M S.Characterization of signals from multiscale edges［J］.IEEE Trans on Pattern Anal Mach Intell(PAM I)，1992，14(7):710 －732.

［15］郭晶.小波分析理论与MATLAB7实现［M］.北京:电子工业出版社，2005:155－156.

［16］陈东明.一种最优小波包基搜寻算法［J］.哈尔滨工业大学学报，2009，41(1):200 －203.

［17］郝久玉.基于小波变换/小波包变换的多载波调制技术［J］.信号与处理，2003，19(1):64 －68.