美式看跌期权定价问题的有限差分直接法

钟坚敏，柴昱洲，孔繁博，汤国斌，秦 僖

(重庆理工大学数学与统计学院，重庆 400054)

期权(Option)是在期货的基础上衍生发展而来的金融工具，其实质是在金融领域中将权利和义务分开进行定价。权利的受让人可在规定时间内对于是否进行交易做出决定，而义务方必须随权利受让人的决定进行交易。在期权的交易时，购买期权的一方称作买方，而出售期权的一方则叫做卖方;买方即是权利的受让人，而卖方则是必须履行买方行使权利的义务人。

期权价格是期权合约中唯一随市场供求变化而改变的变量，它的高低直接影响到买卖双方的盈亏状况，是期权交易的核心问题。

对于欧式期权，John C.Hull等将Black-Scholes定价模型进行了推广，使之可以直接代入定价公式。而美式看涨期权只有到期执行才划算，相当于欧式看涨期权，可直接代入定价公式定价。美式看跌期权可在到期日之前的任何时刻执行，因此不能直接使用定价公式而只能用数值方法来为其定价，这从数学的角度讲就变成了一个在随机过程框架下具有自由边界的求值问题。因此美式期权的定价问题重心转移到其数值解方面，但要得到其解析解并非容易。有限差分的直接方法是计算偏微分方程的有力工具，其核心思想是对各种导数进行离散化，把偏微分方程转化为差分方程。求解金融衍生产品的价格与求解普通的偏微分方程的区别主要在于一般的偏微分方程是给定初值求解终值，而金融衍生产品的定价问题是给定终值求解初值，属于逆向随机微分方程求解。

1 美式期权定价问题基本模型

本文只考虑美式看跌期权的定价问题，主要讨论美式期权定价模型的自由边界问题。从数学上来说，美式期权的定价问题是一个自由边界问题。此处的自由边界是一条需要确定的交界线，它把区域 {0≤S＜∞，1≤t≤T}分成2部分:一部分是继续持有区域，另一部分是终止持有区域。这条自由边界在金融上称为最佳实施边界。显然对每个美式期权的持有者来说，需要知道曲线的位置，以便制订出最佳的实施方案。

基本假设:

1)不付红利。金融资产在期权有效期内无红利及其他所得。

2)风险中性。市场不存在任何套利可能性的条件下，所有可交易证券的期望收益都是无风险利率，未来现金流可以用其期望值按无风险利率贴现，即股票预期收益率μ等于无风险利率r。

3)当前时刻为零时刻。

4)市场无摩擦，即不存在税收和交易成本，所有证券完全可分割。

2 期权定价的有限差分直接法

假设:S表示股票价格;f表示期权价格;r表示无风险利率;T表示期权到期日;Δt表示时间步长，σ表示股票的波动率，K表示期权执行价格;Lf(0，T;X)={u(t)表示股价离散步长;uLf(X)=表示时间离散步数;S=Kex表示等间隔的价格段;t=T－表示股票价格的最高价格。

2.1 隐式有限差分法［2］

2.1.1 隐式有限差分法思路

隐式有限差分法是以有限的离散区域来替代连续的时间和资产价格，可将满足如下偏微分方程的衍生证券

2.1.2 隐式有限差分法算法［2］

首先，把从零时刻(初始时刻设为零时刻)到到期日T时刻之间的时间分为N个等间隔的小时间段，设，就有N+1个时间段。

其次，把资产价格的变化从0到最大值Smax也分成M个等间隔的小价格段，定义，就得到 M+1 个资产价格(0，ΔS，2ΔS，…，Smax)。

算法具体步骤:

2)分析差分方程

将式(2)～(4)代入偏微分方程(1)可得差分方程:

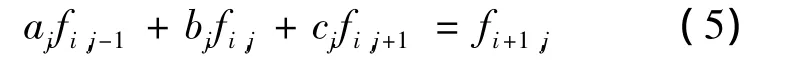
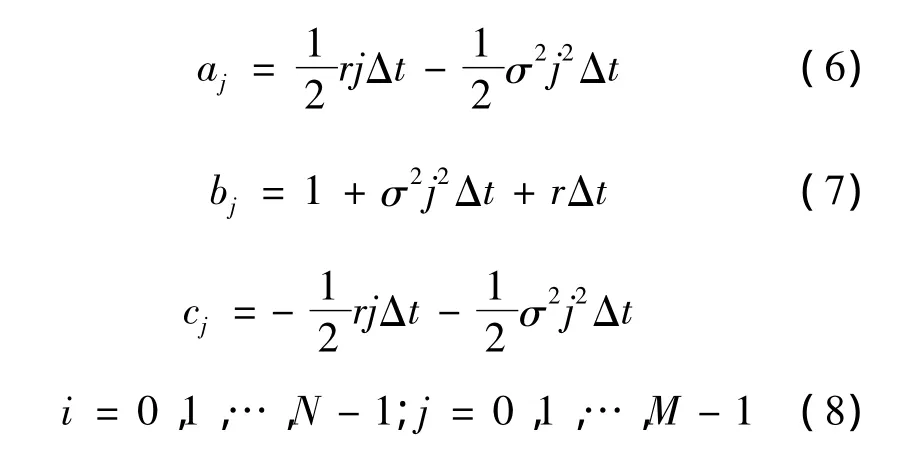
由于使用中心差分［3］，所以整个方程的误差为 o(Δt，ΔS2)。

3)求解期权价值

首先确定股票价格在边界t=T、边界股票价格为0、边界股票价格趋于无穷时的期权价值为

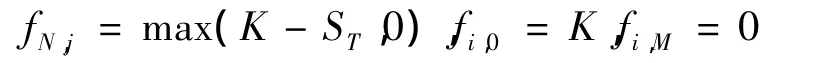
利用差分方程(5)和以上3个边界条件可得出(N－1)Δt时刻的M－1个联立方程:

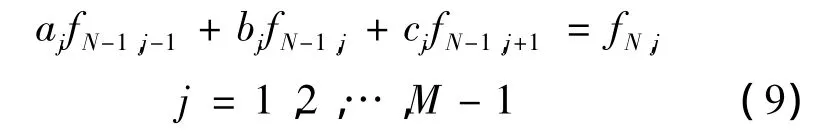
以及:j=0 时 fN－1，0=K;j=M 时 fN－1，M=0。

根据以上各式可求出每个fN－1，j的期权价值，将其与X－jΔS比较得到每个格点的期权价值。所以当jΔS等于资产价格时，该格点对应的f就是要求的期权价值。

2.2 有限差分的直接法

有限差分的直接法是将差分方程(9)转化为矩阵方程来进行求解。这里引入Kronecker积［4］的应用。

定义1［4］设A∈Cm×m，并记A的m个行向量为，于是

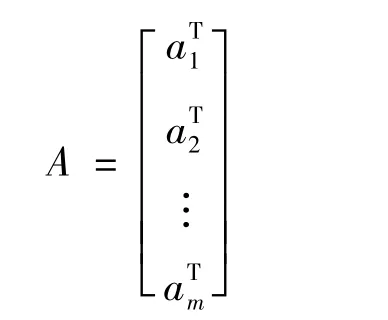
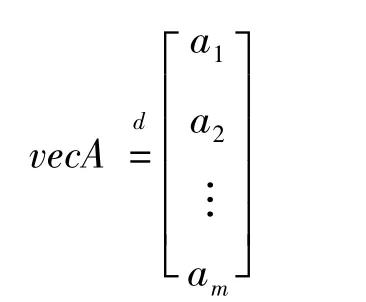
定义vec算符为

定理1［4］设 A∈Cm×m，B∈Cn×n，X∈Cm×n，则有

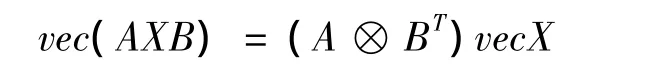
容易证明结论:

推论 1［4］设 A∈Cm×m，B∈Cn×n，X∈Cm×n，则

于是定义矩阵

令

记:

可以得到矩阵方程

解上述矩阵方程，具体步骤:

①利用定理1及推论1，将方程(10)化为与之等价的一般线性方程组

如令 M=A⊗In+Im⊗BT，y=vecF，b=vecC，则式(11)可写成

② 求解方程(12)，所得解y即为每个fi，j期权价值。

3 实例分析

假设标的资产为不付红利股票，其当前市场价为50元，波动率为每年40%，无风险连续复利年利率为10%，该股票5个月期的美式看跌期权协议价格为50元，求该期权的价值。

用隐性有限差分法解决该案例中的期权价值。其中

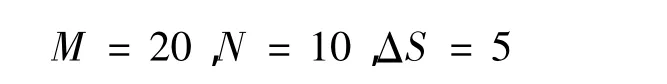
于是可以利用Matlab求出期权价格与期权到期时间的关系，见表 1。可得期权价值为4.072元。

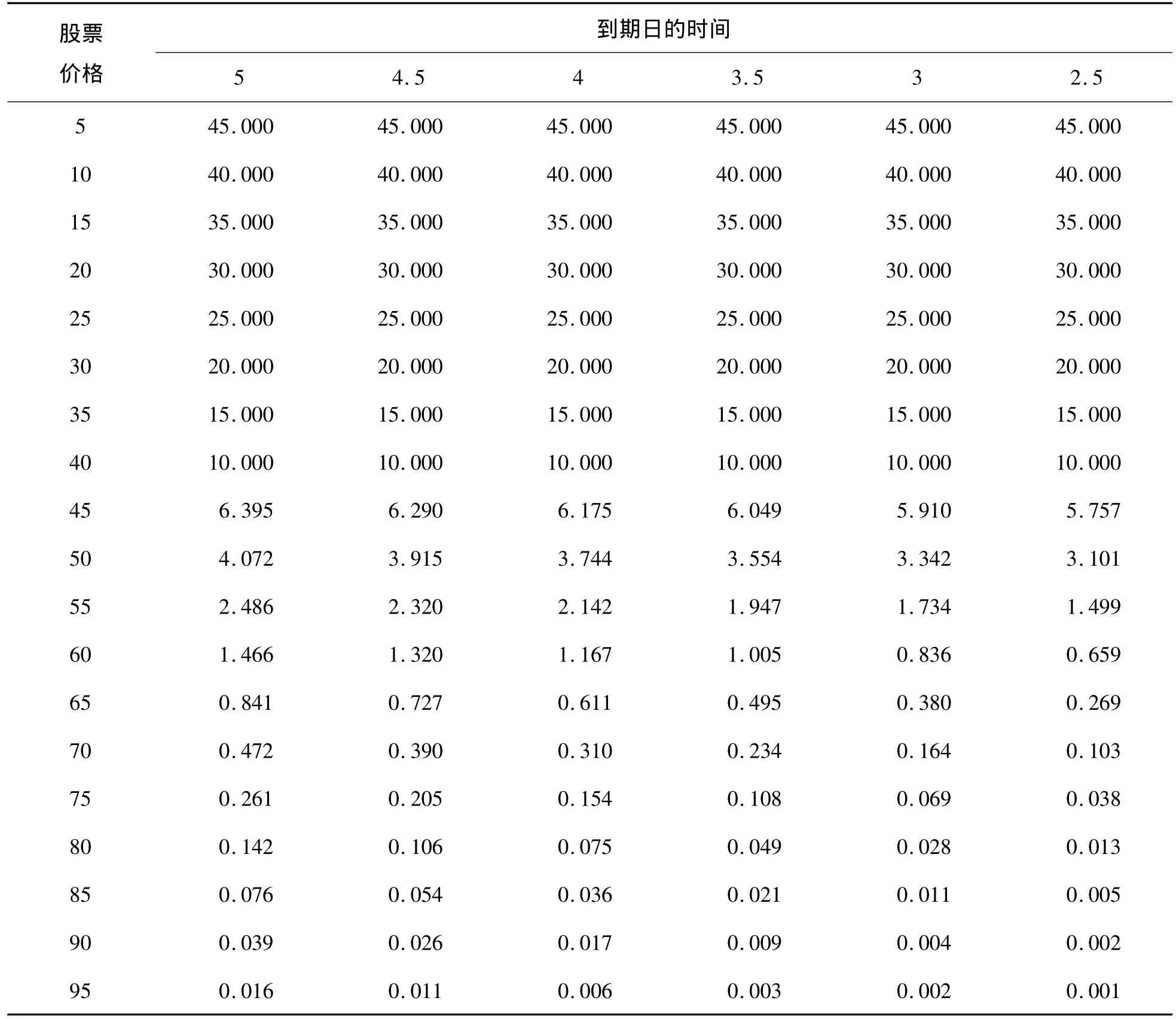
表1 期权价格与期权到期时间的关系

4 结束语

本文主要用隐式差分法对美式看跌期权的定价进行模拟。通过对导数离散化，将偏微分方程转化为差分方程，结合美式看跌期权的边界条件，将差分方程转化为矩阵方程，再利用Kronecker积的应用对矩阵方程进行求解。由于减少了迭代过程中的误差累积，它相对于迭代法计算过程更加稳定，计算结果更加精确。

总而言之，应用Kronecker积，对美式看跌期权的定价进行模拟，其矩阵方程的解直接对应不同时刻 t，不同资产价格 S 下对应的 fi，j(i=0，1，…，N －1;j=1，2，…，M －1)的期权价值，结果较为直观。

［1］郑振龙，陈蓉.金融工程［M］.2版.北京:高等教育出版社，2008.

［2］朱顺泉.金融财务建模与计算——基于 VBA与MATLAB实现［M］.北京:电子工业出版社，2009.

［3］李荣华.偏微分方程的数值解法［M］.北京:高等教育出版社，2005.

［4］陈祖明，周家胜.矩阵论引论［M］.北京:北京航空航天大学出版社，1998.

［5］姜礼尚.期权定价的数学模型和方法［M］.2版.北京:高等教育出版社，2008.

［6］刘敏.美式期权定价的几种数值解法［D］.北京:中国石油大学，2010.

［7］陆金甫，关治.偏微分方程的数值解法［M］.2版.北京:清华大学出版社，2004.