动力定位船舶纵向运动的反步法控制器设计*

张晓兰 王钦若 时丽丽

（广东工业大学自动化学院）

1 引言

随着人类向深海进军，动力定位系统越来越广泛地应用于海上作业船舶、海上平台、水下潜器和军用舰船。它一般由位置测量系统、控制系统、推力系统三部分构成[1]。位置测量系统测量当前船位；控制器根据测量船位与期望值的偏差，计算出抗拒环境干扰力，使船舶恢复到期望位置所需的推力；推力系统进行能量管理并对各推力器的推力进行分配，推力器产生的推力使船舶在风流浪的干扰下保持设定的航向和船位。动力定位系统的核心是控制技术，它标志着动力定位系统的发展水平。

反步法基本思想是将复杂的非线性系统分解成不超过系统阶数的子系统，然后为每个子系统设计部分李雅普诺夫函数(简称V函数)和中间虚拟控制量，一直“后退”到整个系统，将它们集成起来完成整个控制律的设计[2]。它在每一步把状态坐标的变化、不确定参数的自适应调节函数和一个已知 V函数的虚拟控制系统的镇定函数等联系起来，通过逐步修正设定轨迹与实际轨迹之间的偏差，实现系统的全局调节或跟踪，使系统达到期望的性能指标[3]。反步法中引进的虚拟控制本质上是一种静态补偿的思想，前面子系统必须通过后面子系统的虚拟控制才能达到镇定控制的目的。在反步法设计中，最关键的是构造合理的虚拟控制器，消除不确定性的影响。

2 船舶的低频运动模型

在建立船舶数学模型时，分别建立两个坐标系：大地坐标系和随船坐标系。大地坐标系OEXEYE用来计算船舶的运动，坐标原点O任取地球或海面上的某一点，OEXE指向正北，OEYE指向正东。

随船坐标系OXY，其坐标原点与大地坐标系原点相同，根据右手法则，X轴的正向指向船首，Y轴指向船的右舷。有关坐标系的定义如图1所示。

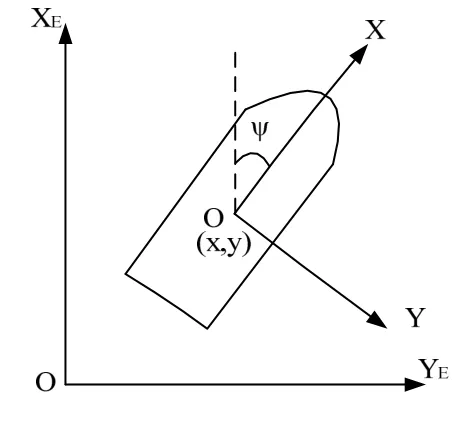
图1 惯性坐标系与随船系

对于动力定位船舶，主要考虑船舶在水平面上的三个自由度运动，即纵荡、横荡和艏摇运动。在随船坐标系中选取船舶速度矢量在大地坐标系中选取船舶位置矢量分别表示船舶的纵荡、横荡和艏摇速度，x、y、ψ分别表示船舶在大地坐标系中的纵向位移、横向位移和艏向角。

由坐标系的定义，可以得出船舶位移和速度的关系式：

其中坐标转换矩阵：

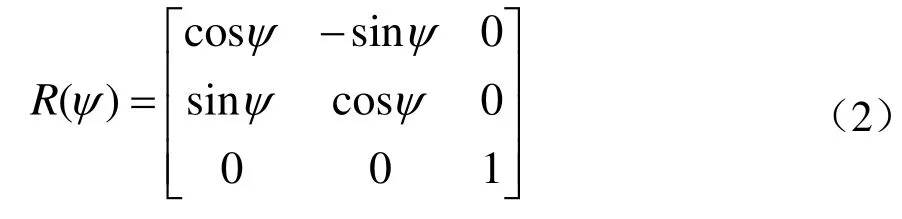
坐标转换矩阵)(ψR是一个非奇异阵，满足：

船舶的低频运动由推进器、风、海流和二阶海浪引起，由Fossen1994年提出的模型结构，船舶在横荡、纵荡、艏摇三个方向的低频运动数学模型如下[4]：

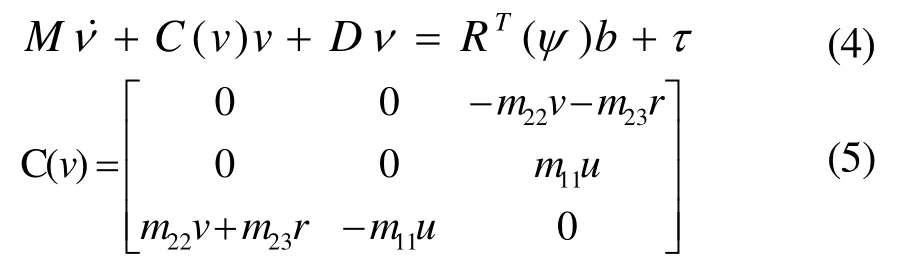
C(v)项表示科氏力和向心力项。科氏力是对旋转体系中进行直线运动的质点，由于惯性作用相对于旋转体系中产生的直线运动偏移的一种描述。

将科氏力和向心力用于模型中，可以改善参数估计的收敛性[5]，但是C(v)项只有在船舶涌动过程中才有意义，对于动力定位船舶来说，在定位模式下的运动速度比较缓慢，C(v)=0。故动力定位船舶的低频运动方程可描述为：

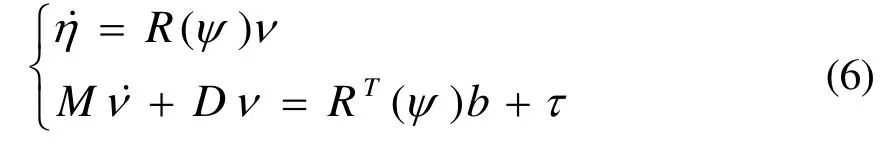
环境扰动作用力主要包括风、浪、流等环境作用力。通常来说，扰动力对船舶运动是相互影响和相互作用的，但在分析过程中，假设扰动作用力的叠加性成立，这样有利于简化船舶动力定位系统模型的建立：

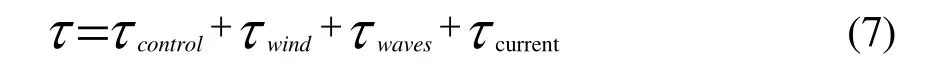
其中，τcontrol为推进力向量；τwind为风力；τwaves为波浪漂移力；τcurrent为海流作用力。

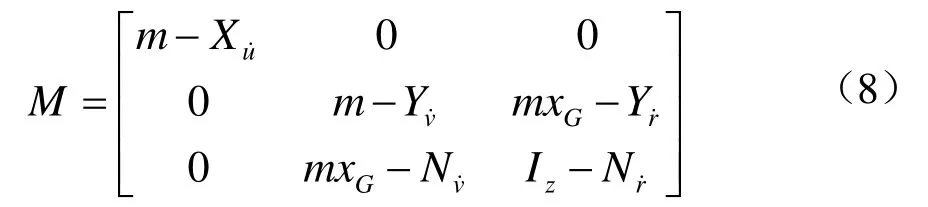
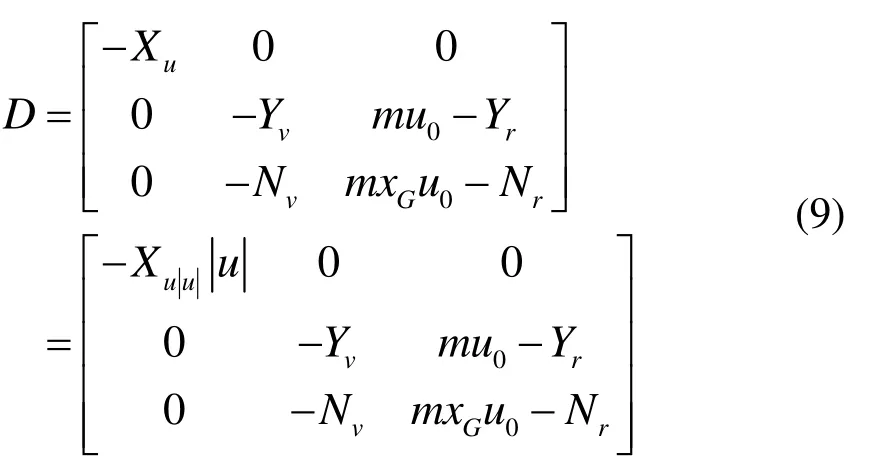
其中，Gx 是船舶的中心和重心之间的距离，阻尼阵D是严格正定的。

b为未建模的动态偏差模型，由风、浪、流引起的未建模的偏差力是缓慢变化的，在船舶控制中，通常用一阶Markov过程表示偏差模型：

3 动力定位系统的反步控制器设计

采用船舶的运动模型如式（6）所示，并假设 b为有界扰动。对式（6）求导可得：

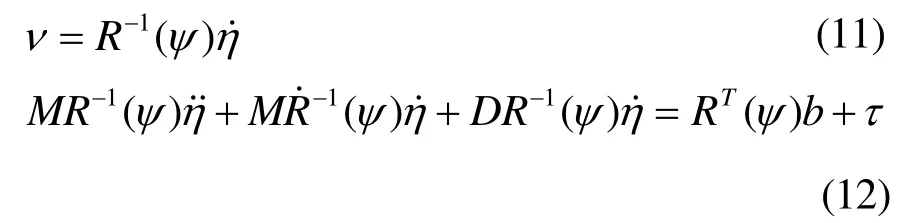
简记式（12）为：

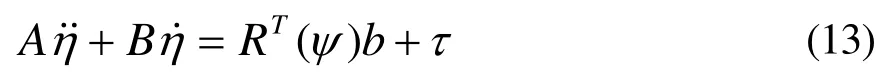
记系统的期望位置为ηd，则系统的偏差量为：

对式（11）求导，并代入式（12）得：

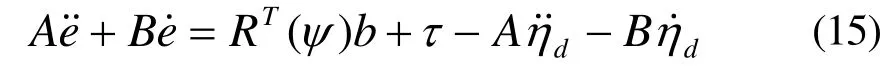
假设：

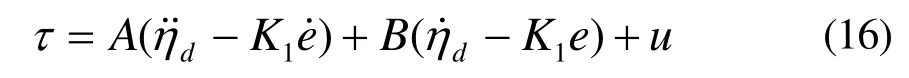
其中，K1为给定值的正定增益矩阵；u为控制输入。

由式（13）和（16），可得误差的动态方程为：

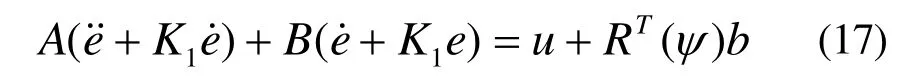
设系统的状态方程为：

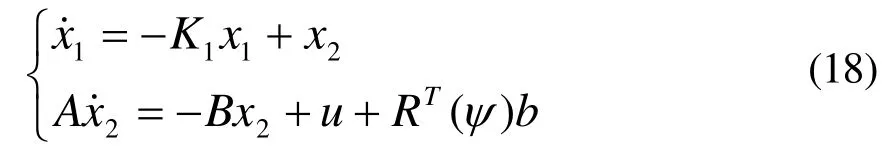
对式（18），选取Lyapunov函数如下：

把 x2看做是虚拟控制量，对其进行反步法设计，使其满足Lyapunov渐近稳定定理，对 V1求导得：

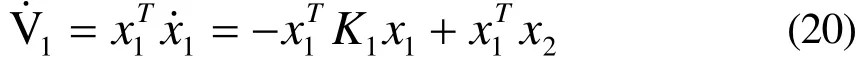
对式（8），选取第二个Lyapunov函数如下：

对 V2求导得：

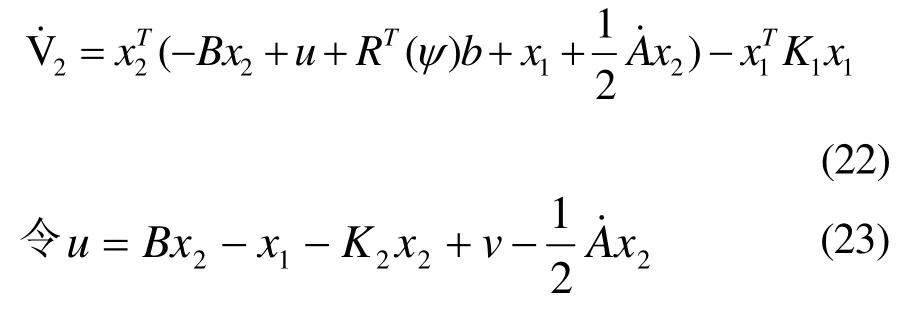
其中，v是为补偿系统的不确定性扰动引入的辅助控制信号，也是待设计量； K2为一正定的对角矩阵。将式（23）代入式（22）得：

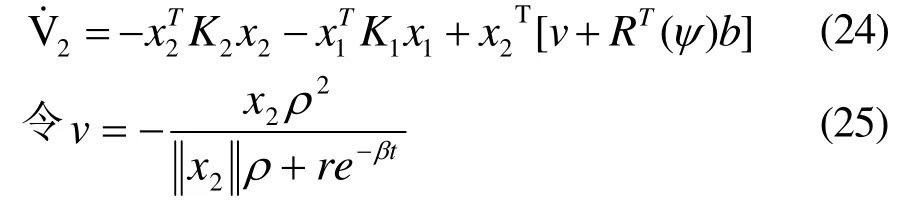
把式（25）代入式（24）得：

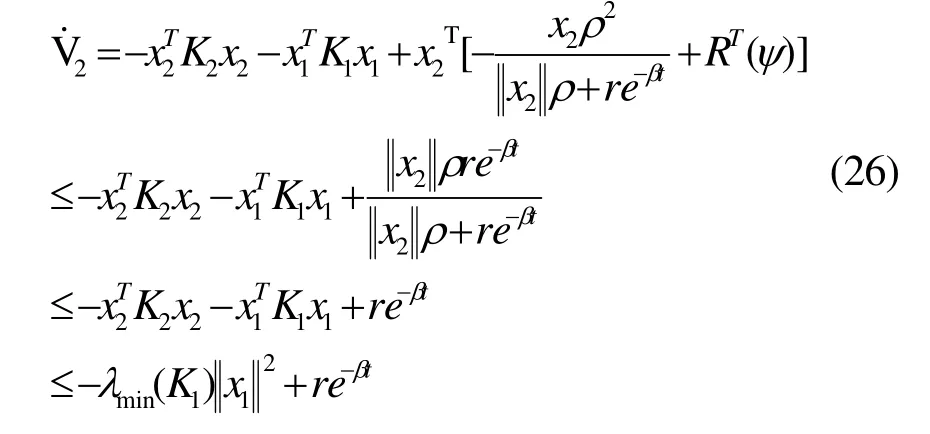
根据Lyapunov稳定性定理， x1x1、 均指数收敛于0，此时的控制律为：

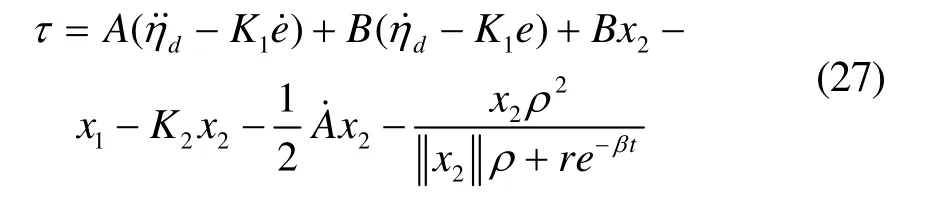
则式（18）是指数收敛的。

4 系统仿真

试验船模参数为：船长2800mm、船宽762mm、船高498mm、船重230kg、方形系数0.652、水线长2691mm、初始航向30°、初始船速1.1kn、重心中心距离200mm，试验船模如图2 所示。

图2 试验船模

根据上述模型计算方法计算船舶在位置坐标为（0，0，0）时的数学模型，得到船模的无量纲惯性参数矩阵和阻尼系数矩阵如下：

未建模的动态偏差模型中的偏差时间常数取为：

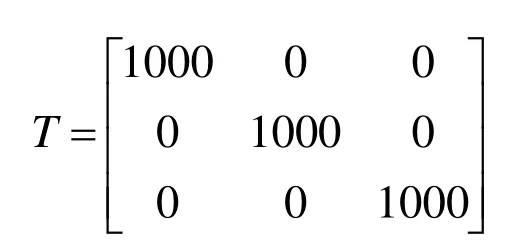
模拟海况为5级（风力6级，浪高2.5m～4m），风向角度60°，均匀来流，流速lm／s，流向角度0°。

在Matlab环境下进行仿真实验，实验结果如图3 所示。

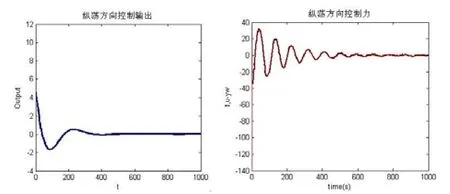
图3 纵荡方向的控制输出和控制力

在设计输出反馈时，可用滤波后的输出值代替测量的输出值，控制器的输入就由过滤后的速度和位置估计值产生，控制效果会进一步提高。

5 结束语

本文在船舶动力定位非线性模型的基础上，提出了基于李雅普诺夫定理和反步法设计了船舶动力定位系统的非线性控制器，保证了控制系统的全局渐近稳定性。仿真实验证明基于Backstepping的非线性控制器应用于动力定位具有良好的控制性能。

[1]贾欣乐,杨盐生.船舶运动数学模型—机理建模与辨识建模[M].大连:大连海事大学出版社,1999.

[2]THOR I. FOSSEN and TRISTAN PEREZ. Kalman Filtering for Positioning and Heading Control of Ships and Offshore Rigs. DECEMBER 2009 IEEE CONTROL SYSTEMS MAGAZINE.

[3]Antonio Loria,Thor I. Fossen and Elena Panteley. A Separation Principle for Dynamic Positioning of Ships:Theoretical and Experimental Results IEEE TRANSACTIONS ON CONTROL SYSTEMS TECHNOLOGY[J],2000,8(2): 332-343.

[4]Thor.I.Fossen. Guidance and control of ocean vehicles. New York:Wiley,1994.

[5]T.I. Fossen,S.I. Sagatun,A.J. Scrensen. Identification of dynamically positioned ships[J]. Control Eng. Practice,1996,4(3): 369-376.

[6]耿矗彬译,MJ摩根著.近海船舶的动力定位[M].北京:国防工业出版社,1984.

[7]冯欣.基于 Backstepping的船舶动力定位系统控制器设计[D].大连:大连海事大学,2009.07.

[8]李殿璞.船舶运动与建模[M].北京:国防工业出版社,2008（1）:53-57.