实心转子同步电动机起动过程研究

杨松 刘晓林

（中国船舶重工集团公司第七一二研究所，武汉 430064）

采用针对电磁场计算而开发的Ansoft EM软件对实心转子同步电动机起动过程进行研究，解决了实心转子电机中瞬态涡流场和机械运动相结合的电磁场、电路及机械系统的耦合问题，得到了合理的工程解释。

1 电机仿真模型的建立

1.1 基本假定及求解区域

为了计算方便，在电磁场求解过程中假设：

（1）电机铁心的轴向长度为无限长；

（2）定转子铁心外缘的漏磁忽略不计；

（3）定子导体和铁心中的集肤效应忽略不计。

整个求解区域如图1所示，采用直角坐标系，由麦克斯韦方程，我们采用矢量磁位求解电磁场问题，在求解区域内矢量磁位A满足涡流方程。

图1 实心转子同步电动机的二维求解区域图

1.2 绕组外部控制电路

在实心转子同步电动机起动过程中，励磁绕组成同心式空间分布在实心转子上，且在起动过程中励磁绕组必须处于闭合状态，满足各绕组电流一致的矢量约束条件；同时，必须正确考虑起动过程中转子槽楔区域铜条的作用。因此，整个仿真试验过程的电路绕组部分涉及到转子限流电阻以及直流励磁电源的切换，仿真结果正确与否，电路模型及相关电路参数的正确设置是关键。

依据同步电动机的异步起动原理，同时根据电机转速设置了简单易用的开关电路（速度函数控制的独立的脉冲电压源控制开关），整个绕组电路如图2所示。

图2 电机绕组及其控制外部电路连接图

其中：Va、Vb、Vc为三相正弦电压源；Vcn1和Vcn2为脉冲控制电压源；LPHASE_A、LPHASE_B、LPHASE_C为定子三相绕组直线部分有限元等效电抗；La、Lb、Lc为定子三相绕组漏电感；Ra、Rb、Rc为三相绕组相电阻；R1、R2为控制电路损耗电阻；V_a、V_lc均为电压表；Ia、I_CON1、I_CON2为各支路电流表；S1、S2为开关。其中，Vcn1、Vcn2分别控制开关S1和S2。

1.3 电机的机械方程

时步有限元法是解决机电系统电磁－机械耦合问题的有力工具之一。磁场的有限元方程、电路方程组以及机械方程的耦合求解能准确地计算磁路的非线性、定子绕组的相间耦合，以及各变量随转速及转子运动位置的变化。电机的机械方程为：

式中：Ω－转子角速度；Tem－电磁转矩；RΩ－阻尼系数；TL－负载转矩；G－转动惯量。

依据仿真环境提供的发电机（电动机）模式，可以给不同的负载转矩，实现不同负载条件下电机的运行仿真。

2 启动性能的计算与分析

2.1 瞬时电磁场分布

涡流问题是实心转子电机中一个普遍存在，但又极为复杂与棘手的问题。它的存在不仅在于产生损耗，而且对电机中的电磁场分布有着直接的作用，对电机的性能产生较大的影响。用二维有限元法计算实心转子磁场分布时，当转子中有涡流产生时，由于挤流效应，涡流一般集中在转子表面的透入深度范围内。本文对一台3150 kW二极实心转子同步电动机进行了分析计算。

图3和图4为空载情况下某一时刻电机中磁场分布图及相对应的电密分布云图。

图3 t=0.4时的磁通分布图

经计算分析，起动初期的集肤现象十分严重，在起动初期转子表面涡流数值很大，转子涡流产生的磁场对电机电磁转矩产生巨大作用；随着转差减小，涡流效应逐渐减弱，当电机稳态运行时转子涡流现象消失。

图4 t=0.4时的电密分布云图

2.2 直流励磁及转速曲线

图5、图6分别为直流励磁作用图和电机转速曲线。由于实心转子转动惯量较大，电机在起动初期转速上升缓慢，不会出现很大的波动，当速度上升到同步速度的95%，脉冲电压源作用，直流励磁电压源串接入励磁绕组电路，励磁绕组电流出现较大的变化，利用直流同步转矩提高电磁转矩，将电机牵入同步运行，当转速达到同步转速后，发生微弱的转速超调现象。

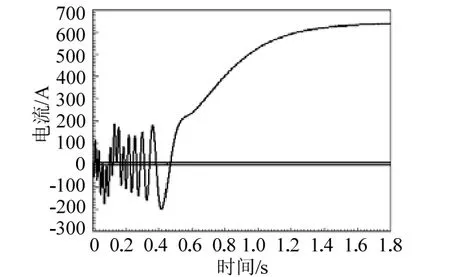
图5 直流励磁电压源作用

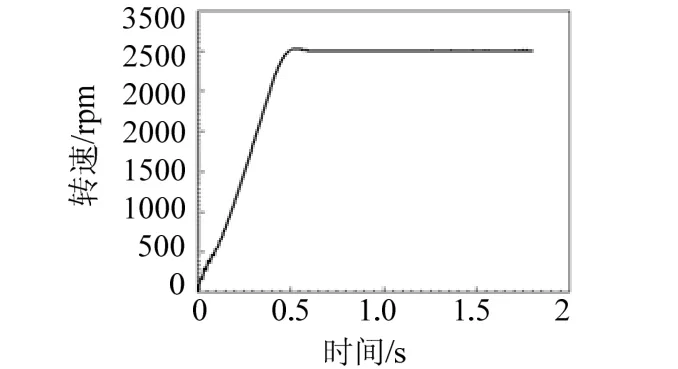
图6 转速随时间变化曲线

2.3 起动电流及起动转矩的分析与计算

图7至图8分别为定子A相电流和电磁转矩随时间变化曲线。从图中可看出，在起动时，定子电流较正常运行要大得多，所以电磁转矩较大。同时由于电机气隙磁场中存在非周期分量，波动幅度较大，出现接近电源频率的脉振，即起动初期转速存在脉动现象。此后，随着非周期分量的减弱直至为零，转矩脉动幅度减小，电机转速缓慢直线上升。在t=0.5 s附近，转速超过同步速度，电磁转矩表现为制动转矩，出现大幅下降现象，短暂的自调整之后，电机进入稳态同步运行。

图7 定子A相电流随时间变化曲线

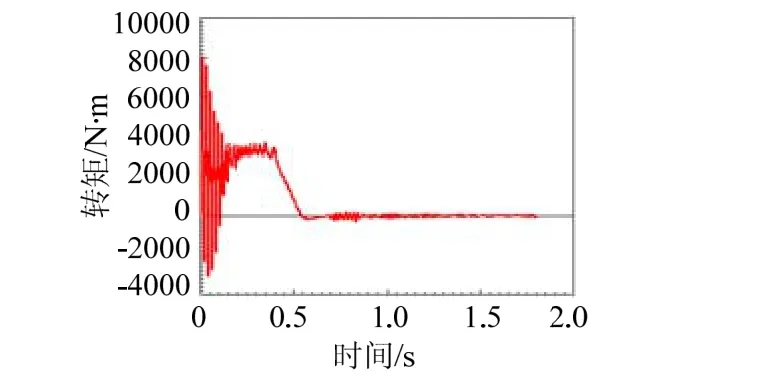
图8 磁转矩随时间变化曲线

经过以上分析并计算，求得起动电流、起动转矩、最大转矩及牵入转矩。如表1所示。显然，实心转子同步电动机具有良好的起动性能和牵入性能。

表1 空载情况下的启动性能

3 结束语

通过“场—路—运动”耦合的实现，求解计算了实心转子同步电动机空载情况下的转子电密分布，起动电流和起动转矩；并通过计算实心转子复合性材料不同电阻率和不同磁导率时的起动电流和起动转矩。得出以下结论：

（1）实心转子同步电动机与普通同步电动机相比较，具有良好的起动性能。

（2）实心转子同步电动机起动过程中的电磁场分布相当复杂，实心转子涡流现象十分严重；随着转差减小，涡流集肤效应逐渐渐弱；稳态运行时，涡流现象基本消失。

[1]唐孝镐, 宁玉泉, 傅丰礼. 实心转子异步电机及其应用. 北京：机械出版社, 1991.

[2]汤蕴璆. 电机内的电磁场. 北京： 科学出版社, 1998.

[3]刘长红, 姚若萍. 基于场路结合的实心转子异步电机转子参数计算. 上海交通大学学报，2003，37(9)：1372～1374.

[4]胡敏强, 黄学良等编著. 电机运行性能数值计算方法及应用[M]. 南京： 东南大学出版社, 2003.