国外利用生长模型预测动物生长及体组分的研究进展

李 勇 蔡辉益 刘国华 常文环 王凤红 中国农业科学院饲料研究所，北京 100081

Zoons等按照建立方法的不同将动物生长模型分为两类，一类为经验性生长模型，一类为机制性生长模型。经验性生长模型主要是通过拟合试验数据得出动物体重随时间变化的函数关系式，借此预测动物的生长。但是，动物的生长是个复杂的现象，其过程受到动物、日粮、环境等多种因素的影响，因而利用简单的经验性生长模型不可能综合考虑所有这些因素，进而准确地预测动物的生长及体组分。机制性生长模型是在考虑动物体组成、营养分配规律、体内蛋白、脂肪沉积规律、体蛋白与体灰分、水分间关系甚至某些生理生化规律的基础上建立起来的，与经验性生长模型相比，它能够更好地处理各种因素对动物生长的影响，从而更准确地预测动物的生长及体组分。正是由于经验性模型的局限性及机制性模型的灵活性，目前较多的研究集中于利用机制性模型预测动物生长。以下即是对两种模型的简要阐述。

1 经验性动物生长模型

1.1 经验性动物生长模型概念

经典的动物生长模型，即经验性动物生长模型是指在非限制饲养条件下，通过对试验数据回归拟合而得到的动物活重随时间变化的函数关系式（或曲线），但是不少学者也提出动物生长模型不应仅描述动物活重与时间的关系，也应包括动物各体组分（蛋白、脂肪、水分及灰分）及各物理体组织（胸肌、腿肌、羽毛）随时间变化的函数关系式。经验性动物生长模型本质上是指动物所能达到的最大生长潜力与时间的关系，它不受环境、日粮等因素影响而仅与动物的基因型及性别有关。

1.2 经验性动物生长模型的发展与建立

自1825年，Gompertz发表了一些关于生长模型的研究以来，动物营养学家对如何建立更为精确的经验性动物生长模型进行了大量研究，表1为目前学者所建立的主要的经验性动物生长模型。Wellock提出了一些评价模型适用性的标准，包括①模型中的参数要尽可能少，而且尽可能具有生物学意义；②模型表达式能够反应出生长速率是动物状态的函数；③模型能够反应出动物的生长是个连续的过程；④模型应该反应出随动物生长体重逐渐维持恒定，在某一时间动物生长速率具有最大值，而相对生长速率则随动物体重的增加逐渐减小直至零。根据这些标准，在众多模型中，Gompertz模型、Logistic模型、Von Bertalanffy模型、Richard模型、Black模型及Bridges模型均为目前比较合理而且能够较为准确反应动物生长的生长模型。其中又因Gompertz模型具有对试验数据拟合效果好、表达式简单而且其中的参数具有生物学意义而被广大研究者所采用。本文也以Gompertz模型为例对动物生长模型所表达的生物学意义进行简单介绍。

表1 主要的经验性动物生长模型

由表1可知，Gompertz模型包含三个参数，分别为A、B和t，A表示动物成熟体重，B表示动物成熟速率，t表示动物达到最大生长速率时的日龄。不同种类的动物只要确定这三个参数便可得到该种动物的Gompertz生长模型。此外，如果以R和U分别表示动物的相对生长速率和绝对生长速率，那么根据 Gompertz 模型，R＝dW/dt/W=Bln(A/W)，U＝dW/dt=BWln(A/W)，从以上两等式可以看出随动物日龄增长，体重（W）增大，相对生长速率逐渐下降，而绝对生长速率则随W的增加出现先增加后降低的变化趋势，这些变化规律与动物实际生长规律相符和，进一步表明Gompertz生长模型描述动物在非限制饲养条件下生长情况的合理性。

正如概念中所提到的，经验性动物生长模型反应了动物最大生长潜力，这类模型的建立需要一个共同的前提，即要求试验数据来源于非限制饲养条件下的动物。非限制饲养条件是一种理想化的饲养条件，在实际试验条件下不可能达到。但是根据Wellock对非限制饲养条件的描述，在建立经验性动物生长模型时动物的饲养条件至少需要满足以下四个方面。①动物能够自由采食；②营养水平及与能量的比例满足动物需求；③采食量不因饲料容重过大或毒素的存在而受到限制；④采食量不因环境因素或动物健康状况，例如温度、疾病等的影响而受到抑制。以此来假设动物处于非限制饲养条件下。

1.3 经验性动物生长模型的应用

经验性动物生长模型是描述动物在非限制饲养条件下生长表现的一种方法，从模型中可以得到动物活重增重规律、动物体蛋白与体脂肪沉积规律及动物体蛋白与体灰分、水分之间的异速生长关系，所以动物生长模型的首要应用就是可以预测动物在非限制饲养条件下的生长及体组分。其次，利用动物生长模型再结合析因法测定动物营养需要的原理，可以预测动物的营养需要。Hruby利用此方法预测了肉仔鸡氨基酸的营养需要，而田亚东则采用此方法建立肉仔鸡能量及氨基酸的动态需要模型。此外，利用动物生长模型可以对动物不同品种间生长差异进行比较，例如，Hancock利用Gompertz生长模型比较并描述了六个商业品种肉仔鸡间的生长差异。

2 机制性动物生长模型

2.1 机制性动物生长模型概念

机制性模型是指以一系列的动物营养理论甚至生理生化理论为基础而建立一套能够预测动物生长及体组分的模型，其中包括了较多的数学关系式，形式上比经验性模型更为复杂。但与经验性模型相比，机制性模型不仅可以预测非限制条件下动物的生长，也可以预测限制条件下动物的生长，即动物实际条件下的生长。

2.2 机制性模型的发展与建立

自从Whittemore和Fawcett较早尝试了构建生长猪的机制性生长模型，并提出了一些构建此模型需要解决的一些理论问题以来，许多学者就构建更为精确、更为合理的猪或鸡的机制性生长模型进行了大量研究。在这些模型中，尽管不同学者所建立的模型在具体细节上有所不同，但都有着共同的理论基础，即对动物生长的描述及营养分割理论。动物的生长既可以指动物各体组织在重量及体积上的增加过程，也可以指各营养素包括蛋白、氨基酸、能量、水分及灰分在动物体内的沉积过程。在建立动物机制性生长模型的过程中，动物的生长通常被看作动物体内蛋白、脂肪、水分及灰分在体内的沉积过程。其次建立动物机制性生长模型，我们必须了解动物营养学中的营养分割理论。营养学认为，动物从饲料中摄取的营养素按其功能可分别用于动物的维持需要、生长需要及生产需要，而且营养素的利用具有一定的先后关系，即营养素首先用于动物的维持需要，然后才用于生长或生产。图1显示了营养物质在动物体内沉积的简单模式。所以根据以上对动物生长的描述，要利用机制性模型预测日粮营养对动物生长及体组分的影响，就必须能够对以下信息进行详细描述。①动物初始体重及组分；②动物日采食量；③动物每日能量与蛋白的维持需要；④日粮营养水平的描述标尺；⑤动物体蛋白沉积的最大速度；⑥动物体蛋白及脂肪实际沉积速率与能量摄入量的关系；⑦动物体灰分及水分的沉积速率。其中，②⑤⑥⑦是模型预测中关键而又难以解决的问题。以下主要对此四个问题进行阐述。

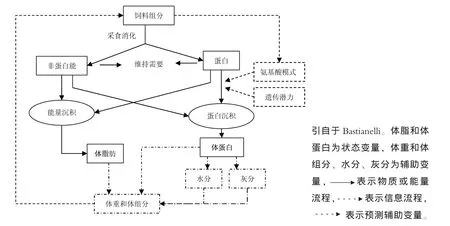
图1 营养分割模型图

2.2.1 动物日采食量预测

动物的生长与动物摄食的日粮密切相关。动物每日采食营养物质的量是机制性动物生长预测模型的驱动变量，所以在环境条件一定的情况下，研究建立动物生长预测模型，首要也是必不可少的一步就是准确预测动物对特定日粮的日采食量。然而，由于动物的采食量受到环境（温度、光照、饲养方式等）、日粮（原料种类、能量及各种氨基酸含量等）及动物自身状态（主要指动物健康状况及体重）等多方面的影响，所以准确估计动物的采食量极为困难。目前，估测猪、鸡等单胃动物自由采食量多数都建立在同样的假设前提下，即动物尽可能采食足够需要的营养物质，一方面用以维持当前生存状态，另一方面尽可能达到自己潜在的生长速率。

在此基础上，Emmans提出要准确预测动物的采食量主要需要解决两个问题：一是确定动物实现最大生长速率对营养物质的需要量。目前多数的研究集中于对能量及蛋白质需要量的研究上。通常是利用析因法将动物需要量分为维持需要及生长需要。生长需要又分为蛋白沉积需要及脂肪沉积需要，例如肉仔鸡每日能量需要量可表达为：MER＝+60Pr+56Fr，其中，MER表示总代谢能需要量，aWb表示体重W时的维持代谢能需要量，Pr为日蛋白沉积量，Fr为日脂肪沉积量；而肉仔鸡每日蛋白需要量可表达为：PR＝0.0233W2/3+Pr/0.85， 其中，PR表示总蛋白需要量，0.0233W2/3表示体重W时的维持蛋白需要量。二是对采食量抑制因子及抑制程度的确定。在预测动物采食量时主要考虑了动物自身肠道的物理容积及动物热损失能力对动物采食量的限制。Emmans和Fisher提出动物能够采食饲料的最大体积与W0.73成一定的比例关系。到目前为止，关于动物热损失能力的报道非常有限，Emmans采用以下公式来估测肉仔鸡的热损失能力：HL＝MBW（a－b）T，其中，HL：肉仔鸡最多可以损失的热量，MBW：代谢体重，a和b为反应动物皮肤隔热能力的参数，T：有效温度（由环境温度、相对湿度及风速决定）。

由上可知，预测动物采食量是个复杂的过程，而目前在一些模型中，对动物采食量的预测简化为仅预测动物每日能量采食量，然后再根据动物日粮中的能量浓度计算动物的日采食量，而对动物每日能量采食量的预测则主要依据动物的体重进行。例如NRC对猪日可消化能摄入量的预测：可消化能摄入量（Kcal/d）＝1250＋188W－1.40W2＋0.0044W3。此外，还有一些模型仅根据采食量与动物活重之间的回归关系来预测动物的采食量。例如Whittermore、Black对生长猪和妊娠母猪采食量预测的回归公式分别为 FI＝0.12W0.75和 FI＝0.111 W 0.803，陈志敏对公母肉仔鸡采食量预测的回归公式分别为 FI＝0.556W0.75 和 FI＝0.5313W0.75。动物采食量受多种因素影响，简单地利用动物体重来预测动物的采食量，具有很大局限性。然而由于此类方法简便易行，所以目前许多动物生长预测模型中仍采用此类方法来预测动物的采食量。

2.2.2 动物体蛋白的潜在沉积速率

Kielanowski及Whittemore和Fawcett分别指出动物每日蛋白沉积存在一个上限，了解这一上限对建立动物生长预测模型有重要作用，因为动物体内富含蛋白的组织含有大量的水分，而水分与蛋白的总量占动物体绝大部分的体重，所以在一定程度上，可以认为蛋白的潜在沉积率决定了动物的潜在生长速率。Emmans利用一个简单的例子说明动物生长潜在速率由动物基因型及动物当前状态（主要指体重）决定，即1kg的肉仔鸡一天最大蛋白沉积可达到60g，而一只100g的肉仔鸡或一只1kg的来航蛋鸡则达不到。同时Emmans指出一定体重的鸡如果要实现潜在的生长速率，必须满足两个条件，即非限制的日粮及环境。Thorbek通过利用对不同体重的猪进行氮平衡试验得到的数据，较早得出了蛋白潜在沉积速率与体重之间的函数关系式：PR＝9.25W0.75－0.166W1.50g/d。这一关系式尽管不是非常精确，但是确实符合动物的实际生长规律：①随动物体重 （W）趋近于0或体重达到成熟(213kg)，体蛋白沉积逐渐趋近于0；②动物体蛋白沉积存在最大值，此时猪体重为85kg。Whittermore和Fawcett同样利用Thorbek数据得到另外一个函数关系式：PR＝60＋1.63W－0.0094W2。 此关系式最大缺陷在于，当动物体重趋近于0时，动物体蛋白沉积仍可以达到60g/d，显然与事实不符。Whittermore为了简化对动物生长的描述，也曾试图利用简单的固定的数值来描述动物的潜在生长速率，不同品种、基因型的动物具有不同的固定数值，这种认为动物蛋白潜在生长速率仅由基因型决定的观点与动物生长规律严重不符，也遭到一些学者的否定，然而仍有一些学者将其应用到动物的生长模型研究中。

除上述函数式之外，Black提出了另外一种描述猪体蛋白潜在生长速率的函数关系式：PR＝aWK((Pm－P)/Pm)g/d。该函数进步之处在于认为动物体蛋白潜在沉积速率不仅与动物当前体蛋白 （P）有关，也与动物成熟体蛋白（Pm）有关。另外，在此函数中，当K为正值时，Wk表示在一定的动物体蛋白（P）条件下，动物体脂肪含量高则蛋白潜在沉积速率一定程度的增大。此后，Black等对这一函数关系式进行了改进，提出与之相关的另一函数关系式用以描述猪体蛋白潜在生长速率即PR＝K （（Pm－P）/Pm）（W＋Ws）a， 其中，K、a、Ws及 Pm 为常数由动物基因型决定，由于该函数具有四个参数（K、a、Ws及Pm）及两个状态变量（W和P），所以此函数具有极大的灵活性。但是Black函数的不足之处在于参数变量多且难以利用试验的方法进行测定。与上述函数形成明显对比的是Emmans根据Gompertz生长函数提出的预测函数关系式：PR＝BPmln(Pm/P)g/d。此函数与Black函数相似之处在于认为动物体蛋白潜在沉积速率由动物当前体蛋白及体成熟时蛋白决定，而较Black函数更为优越的地方在于此函数中除Pm外仅有一个参数B且具有生物学意义。此外，Ferguson和Gous已经显示了如何利用试验方法来估测B和Pm的值。此函数随后被大量学者用于描述动物的体蛋白潜在沉积速率。例如Emmans对火鸡的研究、Kinizetova等对鸡的研究、Kinizetova等对鸭的研究。Whittemore后来也接受并采用了这一函数关系式。正是由于此函数的优越性及通用性，目前成为不少学者所公认的描述动物体蛋白潜在生长速率的函数。

2.2.3 动物体蛋白及体脂肪实际沉积速率的预测

对动物体蛋白及体脂肪进行预测可以分为两步进行，首要的一步是对实际蛋白沉积速率的预测；其次是根据动物每日采食的能量及能量分配理论对脂肪沉积进行预测。Whittermore和Fawcett首先提出了猪每日蛋白沉积达不到最大沉积量时的预测公式：PR＝ep((FI*FCPC*dcp*v)－MP)g/d，其中，ep：日粮理想蛋白沉积为体蛋白的效率；FI：采食量；FCPC：日粮粗蛋白含量；dcp：粗蛋白消化率；v：日粮蛋白相对于理想蛋白的当量值；MP：维持所需的理想蛋白量。从公式中可看出Whittermore和Fawcett是根据动物每日采食的（理想）蛋白量及蛋白沉积效率对实际蛋白沉积速率进行预测，这一思想成为后来预测蛋白沉积的主要思想。同时，Whittermore和Fawcett认为基因型及动物的年龄不影响ep值的大小，并简单地将ep值定为1。根据这一观点，如果动物采食足够低的能量，能量就会被完全用于蛋白沉积，而不进行脂肪沉积，这显然与事实不符。因为即使采食很低的能量，动物体内也有一定的脂肪沉积。所以，Whittermore和Fawcett就对上述观点进行了补充，提出动物机体脂肪与蛋白沉积之间存在一个最小比值（LR：PR）min，这一比值随动物基因型的不同而不同，满足此最小比值之后，蛋白沉积量主要取决于动物每日摄食的蛋白量。尽管这一方法在之后近20年成为预测蛋白沉积的主要方法，并被许多学者应用于动物生长模型中。然而，Whittermore和Fawcett的蛋白沉积预测方法与动物生物实际状况并不相符，因为动物在某些情况下，能够消耗脂肪而沉积蛋白。

近来，Kyriazakis和Emmans提出维持以上理想日粮蛋白用于体蛋白沉积的效率 （净沉积效率）ep直接与日粮能蛋比（代谢能与可消化粗蛋白）成一定的线性关系，直到达到一最大值ep*。此后，随日粮能蛋比增加，净沉积效率维持不变。用公式可以表示为：当 ep

2.2.4 动物体灰分及水分与体蛋白间的关系

动物体灰分及水分的重量常是通过与体蛋白之间的异速生长关系来进行预测。由于动物机体水分含量较多，所以对动物体水分含量的准确预测严重影响对动物机体总重预测的准确性。而灰分含量则较少，所以即使对灰分含量预测出现一定偏差，对动物总体重的准确预测影响不大。目前，动物体灰分及水分与体蛋白间的异速生长关系通常用以下幂函数来表示：ASH＝k1Pakg，WA＝k2Pbkg。 利用简单的幂函数来表述这一异速生长关系并非简单的通过对数据的回归拟合得到，而是具有一定的生物学基础：首先，动物体的这三种组分都与时间呈Gompertz生长关系；另外，三者生长速率参数B相同，所以通过运算可以得出动物体灰分、水分与体蛋白之间呈幂函数关系。Kyriazakis和Emmans及Kyriazakis的等以猪为试验动物进行研究，结果显示灰分预测公式中参数a的估测值为1，k1的估测值接近于0.20，两个值都不随动物基因型的改变而改变，但是k1的值有可能因日粮中蛋白与矿物质的比例不同而不同。同样以猪为试验动物，Emmans和Kyriazakis的试验结果表明，在猪体水分预测公式中，参数b的估测值为0.855，此值不随动物基因型的改变而改变，而k2的值则受猪基因型的影响，与猪成熟体重下的体蛋白含量（Pm）呈一定函数关系。

2.3 机制性动物生长模型的应用

研究机制性动物生长模型最主要是应用于对动物生长及体组分的预测，与经验性生长模型相比，机制性模型并未规定动物必须在非限制性条件下饲养，这就大大增加了预测动物生长的灵活性。King描述了如何利用一种机制性模型 （BPHL）来预测日粮对肉仔鸡生长及体组分的影响。此外结合饲料原料种类及价格等信息，可以开发出相应的商业软件，用于预测动物养殖效益，从而帮助养殖者在实际饲养过程中做出正确决策。

3 结语

关于动物生长模型的研究，近年来国外主要集中于对猪机制性生长模型的研究上，对鸡机制性生长模型的研究相对较少。而国内则主要集中于对动物经验性生长模型的研究上，动物机制性模型方面的研究相对薄弱。针对这种情况和鉴于动物机制性模型在预测动物生长方面具有更为实际的作用，国内有必要在猪鸡等动物机制性生长模型方面展开更为深入的研究。

（略）