适用于低滚降系数成型脉冲的定时恢复方案

黄 磊，许 科，崔慧娟，唐 昆

（清华大学 电子工程系 清华信息科学与技术国家实验室，北京 100084）

位同步是进行可靠数字通信的关键环节。按照定时误差提取方式分类，位同步算法可以分为DA(数据辅助)和NDA(非数据辅助)。相对于DA类算法，NDA类算法不需要引导符号，可以实现更高的带宽有效性，付出的代价是相对较高的估计方差。按照数据处理结构分类，可以分为前馈估计和反馈估计。传统的基于锁相环(PLL)结构的定时估计器都属于反馈估计，由于反馈结构内在特性，使其更容易出现 Cycle Slip和 Hang up[1]现象。本文主要关注NDA前馈定时估计算法。

[2]中提出了一种广泛使用的平方定时估计算法，平方定时估计器基于调制信号的二阶循环平稳统计特性，当成型脉冲的滚降系数较小时，会带来较大的估计方差，本文针对这一问题给出了改进的方法。

1 信号模型和二阶循环平稳特性分析

本文采用标准的脉冲叠加模型，其离散时间版本如下式所示：

w(l)表示独立同分布符号序列，为了便于分析，不妨假设其方差为1;g为成形脉冲，这里采用升余弦成形脉冲，滚降系数为ρ;P表示每个符号采样点数，P取足够大，以保证采样信号不引起混叠;ε表示定时信息，0＜ε＜1；v(n)为独立同分布白高斯噪声。

信号的二阶自相关可以用下式表示：

其中mv(τ)表示噪声的二阶自相关。从上式可以看出，信号的二阶自相关函数是关于P的周期函数，二阶自相关是循环平稳的，所以可以对其求取傅里叶级数，如下式：

G(f)是成型脉冲的 DTFT(离散时间傅里叶变换)，可以看出只要对M2(k;τ)求角就可以求出定时信息。

经典的平方定时估计器[2]可以看作是对M2(1;0)的估计，如下式所示：

其中 vs×s+vs×v+vv×v表示由自相关估计导致的自噪声、信号与加性噪声导致的互噪声及加性噪声的总和。从上式可以看出，定时误差估计变成了一个在加性噪声情况下的相位估计，因此当噪声一定的情况下信噪比主要由G(1;0)决定。对于滚降系数为ρ的升余弦成型脉冲来说，可以得到：

C是一个常量，G2(1;0)与 ρ呈线性关系。当 ρ->0，也就是成形脉冲趋近于Nyquist脉冲时，平方估计法甚至会失败。

2 基于绝对值的定时误差估计器

对于低滚降系数成形脉冲来说，可以采用基于绝对值的定时误差估计器，如下式：

仿真如图1所示。

图1中最下面的曲线是定时估计的MCRB(修正的可拉美罗界)[3]。图1(a)、图1(b)分别对应滚降系数为 0.1和 0.5的 QPSK 调制，分析窗长 L=100时的 MSE=E(ε-)2，可以看出在低滚降系数下，绝对值非线性有明显的性能增益。随着滚降系数的增大，其性能趋于平方非线性。

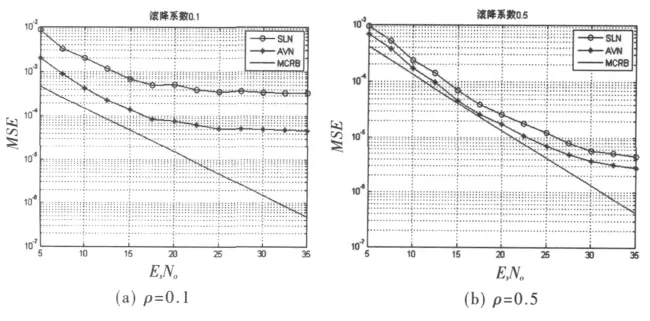
图1 ρ=0.1和 0.5时定时估计均方差与EsNo的关系

其实基于绝对值的定时估计器是基于高阶统计量的定时估计器的特例。对于偶对称无记忆非线性函数，其多项式拟合只包括输入的偶次幂。如式(7)所示：

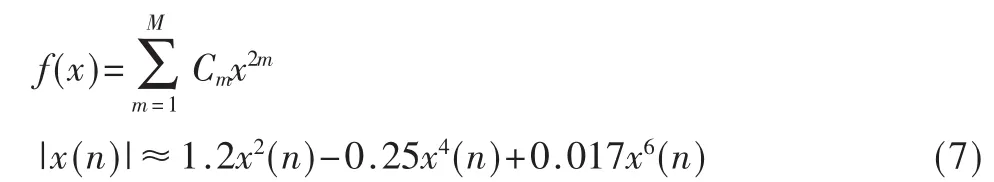
E(x2m(n))同E(x2(n))一样也是循环平稳随机过程，周期为P，运用傅里叶级数可以得到下式：

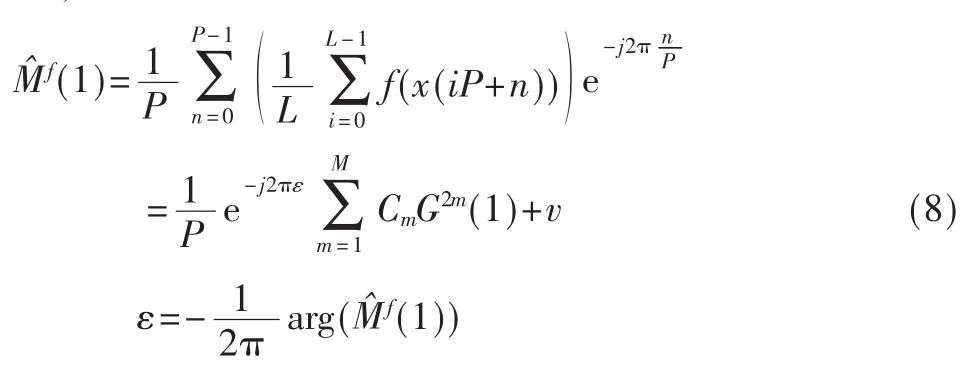
G2m(1)由于解析式太过复杂，可以通过仿真的方法得到，仿真时令ε=0，噪声为0，然后用充分长的序列去估计信号的高阶距，最后进行FFT得到处的值。滚降系数与G(1)的关系如图2所示，矩估计噪声与EsNo的关系如图3所示。

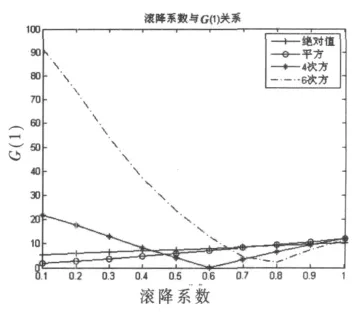
图2 滚降系数与G(1)关系

从图2、图3中可以看出，随着幂次的升高G2m(1)在增大，但是付出的代价是平均矩估计噪声增大，所以只有选择合适加权系数才能实现性能增益。从图2和图3中对比绝对值和平方非线性，绝对值非线性在滚降系数0.1～0.4之间时G(1)值要高于平方非线性，但是平均矩估计噪声并没有显著增加，两者的结合使绝对值非线性在低滚降系数下性能更好。绝对值的G(1)随着滚降系数的增大趋近于平方非线性，在ρ=0.5时两者已经接近。这也与图1仿真是一致的。

3 预滤波和卡尔曼滤波后处理

采用预滤波[4]的方法可以有效降低信号的定时方差，这里采用如下的预滤波器，如下式：

图3 矩估计噪声与EsNo的关系

预滤波和后滤波整体频域响应如图4所示。增加预滤波之后的仿真性能如图5所示。

图4 信道滤波和预滤波整体响应

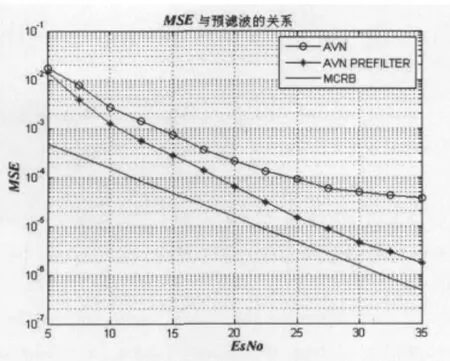
图5 增加预滤波器之后的估计性能ρ=0.1

从图4中可以看出增加预滤波器之后，整体传输特性呈现为一个中心频率在的带通滤波器，通过这个滤波特性提高了在G(1)处的信噪比，改善了估计性能。

除了预滤波之外，基于一阶卡尔曼滤波器的后滤波器可以用来解决定时回绕(Unwrapper)和平滑估计噪声。本文采用参考文献 [5]中的一阶卡尔曼后滤波器结构。通过后滤波可以解决当连续变化的ε超过-0.5和0.5造成的估计反转问题,同时对输出进一步平滑。如图6、图7所示。

本文从信号的循环平稳统计特性入手，分析了传统的平方定时估计器在低滚降系数成型脉冲条件下性能下降的原因。指出绝对值非线性更适合于严重带限信号，绝对值非线性的性能增益源于其可以看作信号高阶矩的加权和，高阶矩的引入改善了由于滚降系数降低带来的性能损失。最后本文指出采用基于频移成型脉冲的预滤波和基于一阶卡尔曼滤波器的后滤波可以有效降低估计方差。预滤波、绝对值非线性和后滤波三者的结合使用可以作为低滚降系数成型脉冲条件下一种合理的定时恢复方案。

参考文献

[1]GERD ASCHEID HEINRICH MEYR.Cycle slips in phaselocked loops:a tutorial survey[J].IEEE Trans.on Comm,1982,COM-30(10).

[2]Martin oerder heinrich meyer digital filter and squre timing recovery[J].IEEE Trans.Comm,1988,136(5).

[3]ALDO N,ANDREA D,MENGALI U.Ruggero reggiannini the modified cramerrao bound and its applicatopm to synchronization Problems.IEEE Trans.Comm,1994,42(21314).

[4]Shi Kai,PRADEEP K.Sarvepalli and erchin serpedin on the design of digital blind feedforward jitter free timing recovery schemes for linear modulations[J].IEEE Trans.on Comm,2004,52(9).

[5]李光源，黄磊，崔慧娟，等.改进的非数据辅助前向反馈符号定时恢复算法[J].电视技术，2011(1):48-50,56.