变值配置函数空间整体编码族的2维对称性

郑智捷

(云南大学软件学院信息安全系,云南昆明650091)

在0-1域中,利用逻辑变量和函数模型进行开关代数分析、设计、描述、优化,以及超大规模集成电路设计和逻辑门阵列实现,通过卡诺图,合取范式,析取范式等方法获得逻辑函数表示[1-4]已有一系列的规范标准[1-8]。这类数理逻辑工具为现代信息和知识产业建立起坚实基础,为先进的电脑和网络技术大规模普及发展做出了实质贡献[1-13]。从形式化逻辑发展的角度,0-1逻辑体系奠定的数理逻辑基础[1-6],推动了当今世界先进科学技术发展的辉煌成就[1-13]。

在复杂性科学[16-20]中元胞自动机模型[16-23]利用逻辑函数递归处理方法,对动态图像变化模式进行深入探讨。在Wolfram开创的“新一代科学”系列研究[24-26]中,除了按照顺序编号观察递归函数的复杂动态特性之外,研究焦点在探寻单个函数反复迭代操作下可能出现的不同图像变化输出模式[16-27]。

离散逻辑函数空间的随机组合带来非规范特性,不同的表示结构对应的变换空间具有内蕴的非数值化特征和巨大组合数目。对整体逻辑配置函数空间进行研究是一类高难度系统探索性问题[16-21,28-32]。

由于缺乏合适的基本原理、模型方法和辅助工具,整体化变换群结构和组织的特性有待于深入研究。利用文献[40-44]中对规则化平面格黑白图像基础和应用研究,提出基本的组织原理和方法。利用多变量0-1序列,从整体编码角度针对变值体系结构等价性和对称性方面进行分析[38-39]。

利用广义和文王等编码系列,形成高维系统分析工具框架,对多变量函数群集提供展示环境。

论文第一章给出基础定义和变值基元的不变特征,第二章对n元逻辑变量建立配置函数空间,引入两类扩展算符：向量化置换运算和互补运算模式。定义了广义编码结构和2维编码表示系列。在第三章和第四章中,应用基元向量结构和变值编码系列,对单个和两个0-1变量的逻辑函数空间进行展示;在第五章中总结所建立的模型和方法。

1 基本定义

1.1 N元0-1序列

令 x=xn-1…xi…x0,0≤i＜n为n元 0-1变量,记 k为指定的关联位置0≤k＜n,输出变量y,n变量函数f,y=f(x),xi,y∈B2={0,1},x∈B={0,1}n

例如：X=01101110,Y=11000111为长度为 N=8的1维0-1序列。最右侧为第0位,最左侧为第7位。

1.2 在逻辑变换中的变值特性

令n元变量序列中的第k个位置为关联位置,在N元序列中,该位置为当前位j,所选定的位置在后继处理中有特殊重要性。

对任意的逻辑变量,在选定了函数之后关联位置形成Xj→Yj点-点对应位置关系。即该模式由当前输入状态和函数输出状态之间建立的关系。

由于关联位置1-1对应取值为 0-1,输入/输出值共有 4类基元变化模式：A：0→0,B：0→1,C：1→0,D：1→1 4类模式,利用变值基元可以建立起更为灵活的表达方式。

例如：逻辑代数的标准范式最大项(1点：B和D类)和最小项(0点：A和C类)传统逻辑析取及合取范式函数是通过选择最大项(1点)或者最小项(0点)集合来决定[1-6],4类变值基元模式以更为丰富的表达形式构成函数方程。

从元胞自动机的角度,当前的输入状态和输出状态是相互关联的。该类关系决定变化基元本身在函数空间中的内蕴特性。

在4类变值模式中,第B和C类对应变值群集;而A和D类对应不变值群集。

2 n元变量状态空间和配置函数空间

N长0-1序列在环转连接下,利用给定位置k的n元变量模式进行操作。

2.1 n元变量和基元状态

令N长0-1序列为环状结构,以忽略序列边界效应,对任意的整数 n,k;0≤k＜n,0＜n≤N,n为变量数目,k为关联点距离最右位的偏移量。随着关联点位置的变动,n元变量在环上对应移动。

输入输出变量的关联状态：

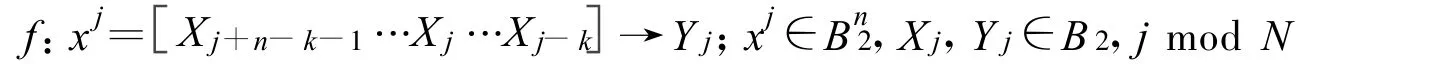
n个输入变量形成一个状态,每个变量取值为0-1,共有2n个状态形成状态空间。

可区分的状态空间在表1中示意。

表1 基元向量及其状态编号

n变元独立取值,共有2n可区分状态,每个状态编号 I数值的0-1取值对应着一个给定的n元状态向量。第I个基元向量,在系统中2n基元向量形成基元向量空间。

函数空间及表示向量

记J=J2n-1…Jj…J0,0≤j＜2n,Jj∈B2,为长度为2n位的函数向量,每个函数向量 J确定一个逻辑函数,共有向量构成函数空间在表2中示意。

表2 函数向量及其函数编号

2.2 顺序编码-邵雍-Leibniz编码

在公元11世纪,邵雍首先提出按二叉树形成的顺序排列黑白图像表示方法[33-37]。在公元17世纪,Leibniz使用0-1序列将树状黑白图像模式表示成二进制算术表示[15,32]。

定义2.2.1：邵雍-Leibniz编码(SL码)为函数表中按二进制编号顺序排列的序列

证明：按照二进制计数的模式,在每个编号向量中1值对应最大项,0值对应最小项。所选择的编号值集合和函数形成1-1对应关系。

2.3 1维编码-广义编码和配置函数空间

记Ωm为m元对称置换群结构。

令P为置换算符,

定理2.3.1：在置换算符P的作用下,所有的可区分的2n!置换函数向量组成一个逻辑函数向量置换群空间。

证明：置换算符作用在特征向量上,向量共有2n不同位置,第0个位置有2n种选择,…,第 j位置有2n-j种选择,…,第2n-2位置有2种选择,第2n-1位置仅有1种选择方式。可能的总数目为各个位置选择数目的乘积。

对每个基元向量的位置可以选择原来的值,或者为相反的值。定义互补运算Q,在向量的模式下,令Q为一个2n长0-1向量,P(J)Q=P(J2n-1)Q2n-1…P(Jj)Qj…P(J0)Q0

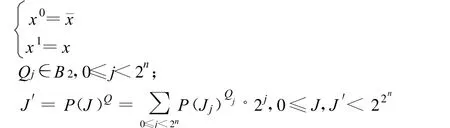
为方便描述,在P和Q两类算符作用下形成的空间称为配置函数空间,一个选定的P和Q算符确定一个配置函数,每个配置函数包含按广义编码排列的个函数。

定义2.3.2：广义编码(G码)是由P和Q算符对2n位长向量J作用后,形成的配置编码模式。

定理2.3.3：在P和Q两类算符作用下,广义编码P(J)Q所包含的可区分配置函数数目为

证明：对每个互补运算j,Qj有两种选择,Q的选择总数为;对置换算符基元向量在P算符的作用下形成2n!置换群,总数目为二者的乘积。

广义编码配置函数的数目为n元逻辑互补空间的算符数目与2n个基元置换对称群算符数目的乘积。

2.4 二维编码

广义编码,在P,Q变换下所形成的编号还是22n向量的一个置换,在配置函数变换空间中存在置换,将其重排为与SL编码对应的顺序编号模式。

为方便地描述2维结构,

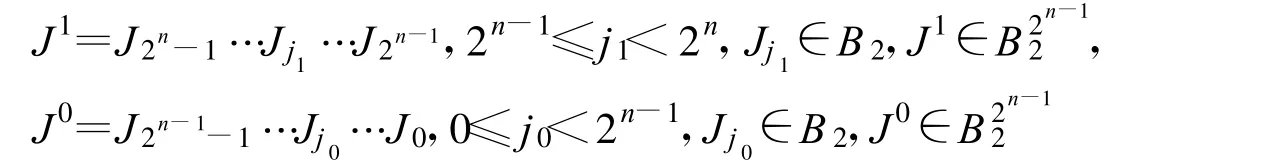
令P(J)Q=P〈J1|J0〉Q形成二维编码。

公元前13世纪,周文王(姬昌)首先引入了非对称排列,将八卦图示表示为两个置换群集[33-37]。用文王命名这类形成二维表示的编码结构。

定义2.4.1：文王码(W 码)为满足 P(J)Q=P〈J1|J0〉Q条件,形成的通用型二维编码。

定理2.4.2：文王编码等价于广义编码,文王编码提供一个2维平面框架显示选定的配置函数中各个函数的相对位置。

证明：每个广义编码的编号能写为〈J1|J0〉文王编码的标准形式,在表3中每个逻辑函数在配置函数表示空间中有一个确定的位置,

表3 2维展示框架

通过文王码的两个子编号,将函数集展示在2维平面上。

表4 n=1广义编码和文王编码序列

二维广义编码排列为：

如何才能激发学生学习的愿望，教师在设计练习时要充分考虑儿童的心理特点，教师结合学生已有知识尽量使练习设计新颖，生动有趣，只有有趣的练习，才能调动学生做练习的积极性。

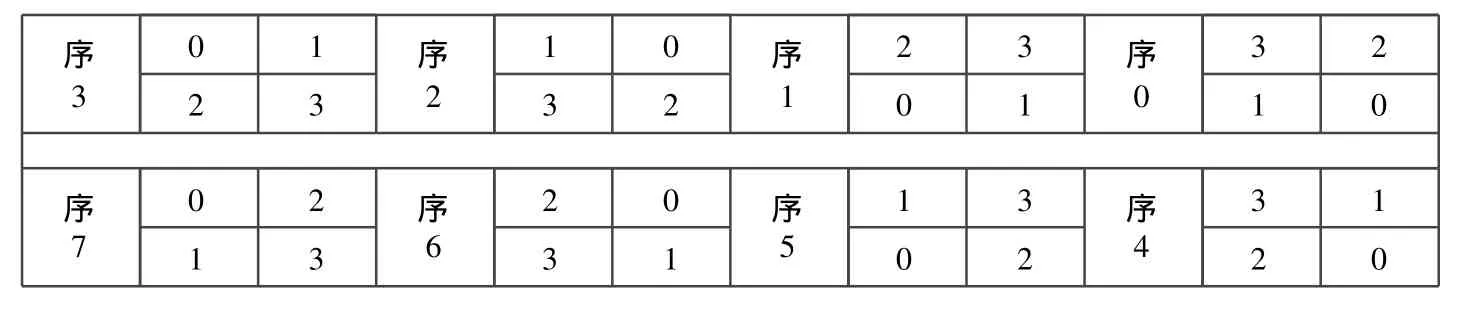
序3 0 1 1 0序2 2 3序1 3 2序0 2 3 3 2 0 1 1 0序7 0 2 2 0序6 1 3序5 3 1序4 1 3 3 1 0 2 2 0

8个二维表不同函数排列：

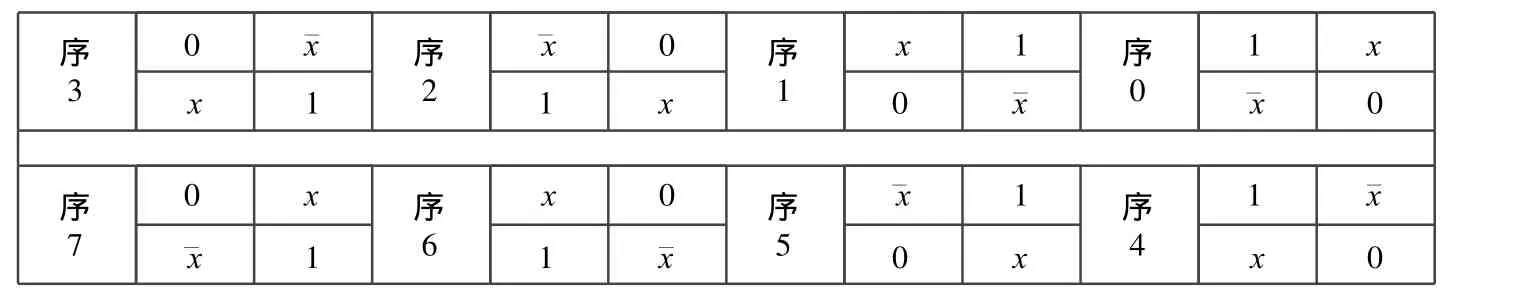
序3 0 ¯x¯x 0序2 x 1序1 1 x序0 x 1 1 x 0 ¯x¯x 0序7 0 x x 0序6¯x 1序5 1 ¯x序4¯x 1 1 ¯x 0 x x 0

置换和互补运算不会改变函数本身,但将不同的配置函数排列成可区分的结构。这样不变特性为整体分析提供分析比较图式。

2.5 伏羲编码和共轭编码

公元前45世纪,伏羲排出对称编排的八卦模式[33-37],用伏羲命名这类配对的对称编码。

定义2.5.1：对2维文王编码,如果∀j1-2n-1=j0,0≤j0＜2n-1,2n-1≤j1＜2n同时Ij1=¯Ij0,即两个相差2n-1的基元按照配对的模式排列互为互补向量表示,则该类编码为伏羲编码(F码),也称为广义共轭编码(GC码)。

如果还有更强地约束基元配对,则形成另一类编码。

定义2.5.2：在伏羲编码系列中,如果对∀Ij0∈IJ0,对基元特定的位置i,,(或者∀Ii=1),0≤i＜2n-1,则该类编码为共轭编码(C码)。

在配对条件下的两种编码有如下定理。

定理2.5.4：对n元变量结构,C码的数目是8×(2n-1)!

证明：基元向量互补算符Q共有4种可能性。由于置换算符P前一半的基元同后一半的基元有配对要求,同时对基元特定的位置i,∀Ii∈Ij0&Ii=0,(或者∀Ii=1)0≤i＜n,一共有!组合。两类算符相互独立,编码总数为两者数目的乘积。

2.6 几种编码方案比较

为了比较不同的编码系列,在表5中列出主要编码和计算公式。以判断编码的整体特性。

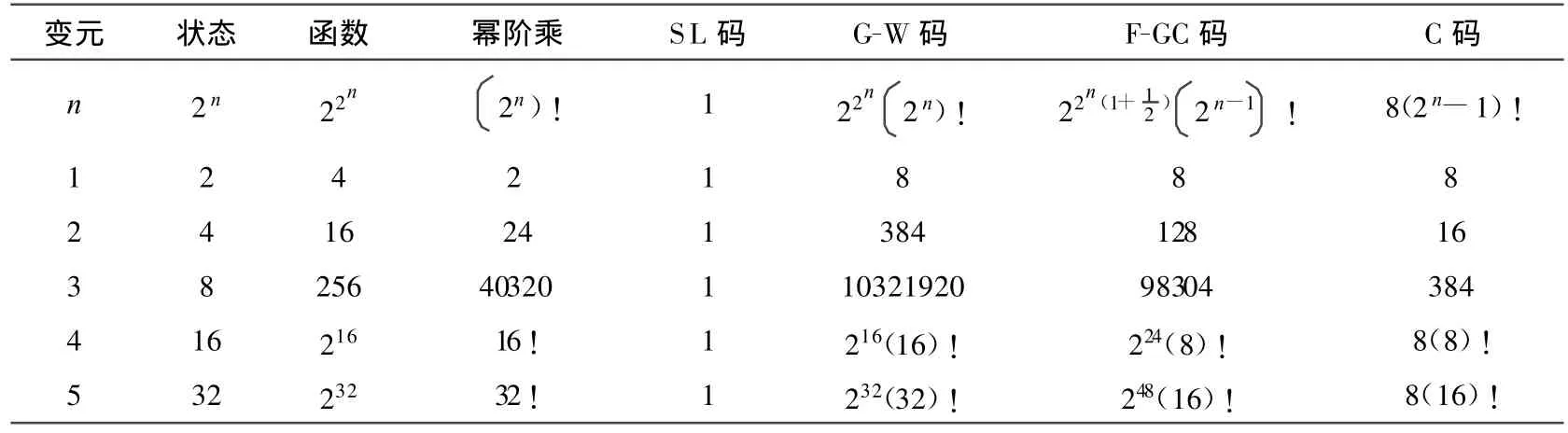
表5 不同编码计算公式比较

在单个变元的条件下,8个G-W码序列也是F-GC码和C码序列。

随着变元数目超几何级数增长,详细研究只可能针个例,不能进行穷举性遍历。

在下面的章节中,研究单变量和双变量的配置函数空间展示分布情况。

3 单变量和双变量的表示结构

3.1 基本模式

对单变量函数,

单元函数为1-1变换关系,按照公式

对输入变量在输入向量上求值,得到函数的输出序列。

对双变量函数,将首尾衔接成环状,由于变换的非对称性有两种变换模式：

类型A：

或者

类型B：

或者

3.2 单变量配置函数空间

从逻辑代数的角度,单变量函数是最基本的函数。函数空间表示如下：令 x为逻辑变量x∈{0,1}

在一元逻辑函数空间中有4个函数,编号为0-3。在单变量下,各类编码都是相同的,考察SL码和C码的编号排列。

3.3 单变量函数的SL编码和C编码表示

对单变量函数,用如下的规则构造其表示空间：

(1)将状态空间分为两个集合：0,1;

(2)按照选择及不选择,在函数空间中建立关系;

(3)在状态集合1,0上,互补10,01集合在〈J1|J0〉模式中标记为编号;

(4)记 f(〈J1|J0〉|x)的基本结构〈J1|J0〉为选择的变值函数表示：

y=f x x ¯x 10 01 〈J1|J0〉 C码编号 等价函数 SL码编号f0(x)=f00(x)0 0 1 0 〈1|0〉 2 0 0 f1(x)=f01(x)0 1 1 1 〈1|1〉 3 ¯x 1 f2(x)=f10(x)1 0 0 0 〈0|0〉 0 x 2 f3(x)=f11(x)1 1 0 1 〈0|1〉 1 1 3

其他函数的等价特性关系,亦能通过选择集合验证。

3.4 共轭表示的定理和推论

从3.3节中可以看到,利用最大项或者最小项组合所构成的函数,与通过变值基元构成的函数是相互等价的。两个配置函数空间具有同样的大小,不同的编号和函数可以相互比较。

从基元变换群的角度,基元状态形成变值基元。这样的描述特征有利于克服经典系统适合表达静态组合特性而缺乏动态描述功能的局限。

利用对应关系,得到等价性定理。

定理3.4.1：单变量逻辑函数空间和单变量变值函数空间的可区分函数总数为221=4。在两个结构中的4个函数1-1对应。

证明：利用4个函数的对应关系,等价性成立。

在结构中形成的4个顶点有明确地意义。

推论3.4.2：在变值表示中,4个函数有如下的变换意义,

(1)f(〈0|1〉|x)保持{1}点状态不变,转化{0}点为1。对应逻辑代数的1函数;

(2)f(〈0|0〉|x)保持原有的值不变。对应原函数 x;

(3)f(〈1|1〉|x)将{0}点转化为1值,同时将{1}点转化为0值。对应逻辑代数的非函数¯x;

(4)f(〈1|0〉|x)保持{0}点状态不变,转化{1}点为0值。对应0值函数。

证明：对1元逻辑函数,只有上述4种情况。

推论3.4.3：1元函数的函数空间同变值函数空间同构。

证明：在两个结构中任意函数明确的1-1对应。

应用例子

对给定的0-1序列 X=01101110,8位长的二进制序列,1元共轭函数空间生成如下4种输出序列：

4 双变量的表示结构

对任意n变量,状态数目为2n,函数空间数目为。在双变量函数空间中共有16个函数。

4.1 A型双变量表示

对A型模式,序列X,下列关系成立：

f x 0 1 z 0 1

双变量 x,z一共有4种状态组合：

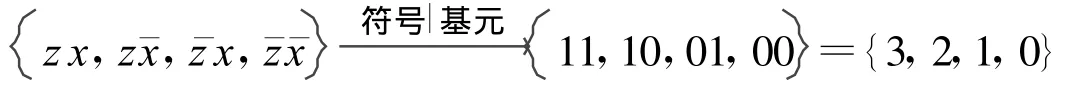
16个函数的不同编码在表6中示意。

对双变量函数,用如下的规则表示：

(1)将zx的状态空间根据x点取值为0或者1分为两个集合：{0,2},{3,1};

(2)状态集0：3;2：1是共轭对;

(3)由1(0)点状态决定J1(J0)的集合;

(4)选择状态为1,不选择为0,建立对应关系;

(5)〈J1|J0〉为变值表示：f(〈J1|J0〉|zx)

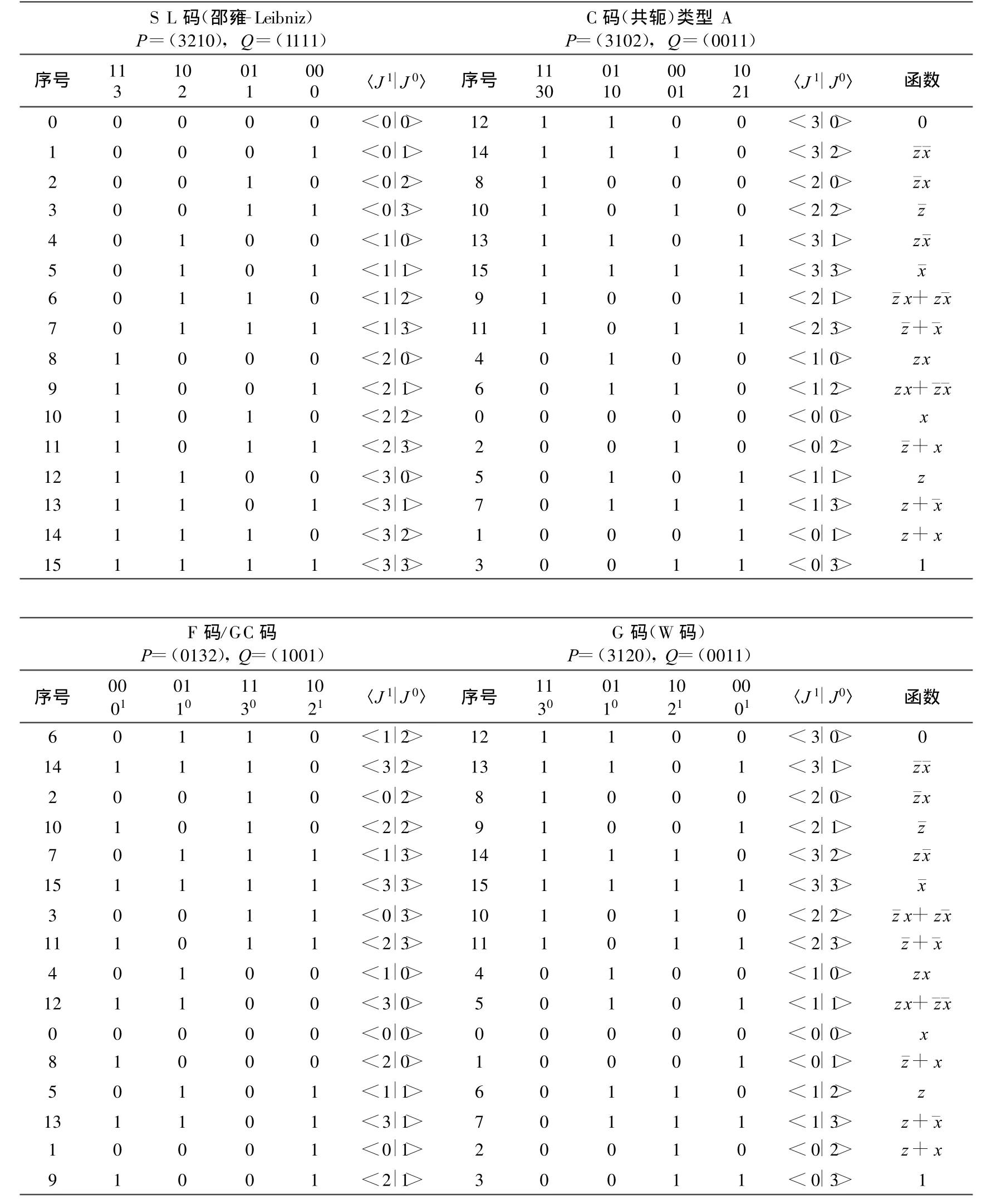
表6 1维排列SL C(类型A),F,G,W 各类表示

二维展示：

SL码顺序排列 SL码函数分布

二维码排列 F码函数分布＜0,0＞ ＜0,1＞ ＜0,2＞ ＜0,3＞ x z+x ¯zx ¯zx+z¯x＜1,0＞ ＜1,1＞ ＜1,2＞ ＜1,3＞ zx z 0 z¯x＜2,0＞ ＜2,1＞ ＜2,2＞ ＜2,3＞ ¯z+x 1 ¯z ¯z+¯x＜3,0＞ ＜3,1＞ ＜3,2＞ ＜3,3＞ zx+¯z¯x z+¯x ¯z¯x ¯x W码函数分布 C码函数分布x ¯z+x z+x 1 x z+x ¯z+x 1 zx zx+¯z¯x z z+¯x zx z zx+¯z¯x z+¯x¯zx ¯z ¯z x+z¯x ¯z+¯x ¯zx ¯zx+z¯x ¯z ¯z+¯x 0¯z¯x z¯x ¯x 0 z¯x ¯z¯x ¯x

将得到的结果,总结为定理形式。

定理4.1.1：对多元变量等价变值函数集表示,SL编码不同于C编码的排列模式。

证明：观察SL码的基元向量,当变元数目大于1时。按顺序排列的前一半和后一半向量通常不会满足广义共轭条件。

定理4.1.2：对任意的F编码,按主对角线划分,对应编号的函数为成对共轭函数。

证明：在F编码条件下,任意选择的编号〈J1|J0〉其在对角线另一侧的编号是〈J0|J1〉。该编号是原向量集的共轭变量集合。

观察上面例子中的F码和C码的函数分布,函数对满足成对共轭关系。

定理4.1.3：对任意的C编码,除了主对角线的共轭对称性之外,4个顶点为：0,x,¯x,1

证明：在上述4种情况中,x什么都不变自然保持输入变元原状态直接输出;1函数将0点变为1,输出1向量;0函数转化1点为0,输出0向量;¯x把0点变为1,同时 1点变为0,输出为原值求反。

4顶点不变性是C类编码特有的空间结构特征。

定理4.1.4：在文王编码中如果基元向量集无成对匹配,则其对应函数分布一般不出现共轭对称效应。

证明：由于编码规则的约束,非成对匹配形成非对称排列。但可能在一些团体组合模式下以个例显现共轭对称性,定理的结论对大部分情况能够成立。

观察前面G码的例子,尽管大多数函数对非共轭对称,但是两个顶点函数(0和1)仍保持共轭对称。

5 结论

对多变量条件下利用传统东方逻辑结构建立起现代化变值逻辑变换体系。利用变值基元向量,建立了整体编码模型和系列化编码展示结构。

定理4.1.1-4.1.4总结论文的主要结果。在新的编码系列中,文王编码具有通用二维结构。伏羲编码在配置函数空间中形成共轭函数对。而共轭编码,特有的四元极值顶点将其他的编号约束在内。

由于文王编码系列具有超几何级数增长的趋式,下一步的工作将集中在对较少量变元(2-4)的变换结构进行实际的模拟处理和穷举型计算。同时应用该理论体系处理数学/物理的基础悖论问题,为实际应用现代东方逻辑系统：变值逻辑体系开辟道路。

致谢：感谢已故的恩师高庆狮院士,高先生早在30年前就指导作者在对称置换群上构造并行算法。感谢陈涛先生利用分层结构化模型建立的现代中医辅助诊断系统,应用传统中医理论形成现代化成果激励作者重返基础逻辑研究前沿。感谢云南省特色专业建设基金和云南省软件工程重点实验室信息安全专项基金支持。

[1]杨炳儒.布尔代数及其泛化结构[M].北京：科学出版社,2008.

[2]S P Vingron.Switching Theory：Insight Through Predicate Logic[M].Springer,2004.

[3]秦军南.开关理论与逻辑设计[M].北京：人民教育出版社,1980.

[4]Saburo Muroga.Logic Design and Switching Theory[M].Wiley-Interscience Publication,1979.

[5]A Kandel,Samuel C Lee.Fuzzy Switching and Automata：Theory and Applications[M].Crane Russak&Company Inc,1979.

[6]Samuel C Lee.Modern Switching Theory and Digital Design[M].Prentice-Hall Inc,1978.

[7]F H Edwards.The Principles of Switching Circuits[M].MIT Press,1973.

[8]霍书全.多值逻辑的方法和理论[M].北京：科学出版社,2009.

[9]石纯一.数理逻辑与集合论(第二版)[M].北京：清华大学出版社,2000.

[10]胡世华,陆钟万.数理逻辑基础[M].北京：科学出版社,1981.

[11]金岳霖.形式逻辑[M].北京：人民出版社,1979.

[12]数理逻辑论文选：第一集,1958.

[13]A B Rosser,A R Turquette.Many-valued Logics[M].North-Holland Publishing Company,1952.

[14]桑靖宇.莱布尼兹与现象学[M].北京：中国社会科学出版社,2009.

[15]阎莉.整体论视域中的科学模型观[M].北京：科学出版社,2008.

[16]雷功炎.数学模型八讲[M].北京：北京大学出版社,2008.

[17]宣慧玉,张发.复杂系统仿真及其应用[M].北京：清华大学出版社,2008.

[18]李士勇.非线性科学与复杂性科学[M].哈尔滨：哈尔滨工业大学出版社,2006.

[19]涂序彦,尹怡欣.人工生命及应用[M].北京：北京邮电大学出版社,2004.

[20]H Umeo,S Morishita,K Nishinari.Cellular Automata[M].Springer,2008.

[21]江志松.122号初等元胞自动机的复杂性分析[J].科学通报,2000,45(18)：2007-2012.

[22]D Griffeath,C Moor.New Constructions in Cellular Automata[C].Santa Fe Institute Studies in the Sciences of Complexity,2003.

[23]A Ilachinski.Cellular Automata-A Discrete Universe[M].World Scientific,2001.

[24]S Wolfram.A New Kind of Science[EB/OL].http：//www.wolframscience.com,2002.

[25]S Wolfram.Cellular Automata and Complexity.Addison-Wesley,1994.

[26]S Wolfram.Theory and Applications of Cellular Automata.World Scientific,1986.

[27]李元香.格子气体自动机[M].北京：清华大学出版社,1994.

[28]金日光.模糊群子论[M].哈尔滨：黑龙江科学技术出版社,1985.

[29]Wiktor Marek etc.Elements of Logic and Foundations of Mathematics in Problems[M].PWN-Polish Scientific Publishers,1982.

[30]A Thayse.Boolean Calculus of Differences[M].Springer-Verlag,1981.

[31]J Fogarty.Invariant Theory[M].W.A.Benjamin,Inc.,1969.

[32]Paul Benacerraf and Hilary Putnam[M].Philosophy of Mathematics Prentice-Hall Inc.,1964.

[33]互子.易道中互-易经体系[M].广州：花城出版社,2009.

[34]徐芹庭.易图源流[M].广州：中国书店,2008.

[35]黄宗羲.易学象数论[M].北京：九州出版社,2007.

[36]张一方.中华历代易学家传[M].北京：北京艺术与科学电子出版社,2007.

[37]施维.周易八卦图解[M].成都：巴蜀书店,2005.

[38]Zheng Jeffrey,Zheng Chris,Kunii T L.A Framework of Variant-Logic Construction for Cellular Automata,Cellular Automata-Innovative Modelling for Science and Engineering[M].InTech Press,2011：325-352.

[39]Zheng Jeffrey,Zheng Chris.A framework to express variant and invariant functional spaces for binary logic[J].Frontiers of Electrical and Electronic Engineering in China,2010,5(2)：163-172.

[40]Z J Zheng.Conjugate Visualisation of Global Complex Behaviour[J].Complexity International,1996,(3).

[41]Z J Zheng,C H C Leung.Visualising Global Behaviour of 1D Cellular Automata Image Sequences in 2D Maps[J].Physica A,1996,233：785-800.

[42]Z J Zheng.Conjugate Transformation of Regular Plan Lattices for Binary Images[D].PhD Thesis,Monash University,1994.

[43]Z J Zheng,A J Maeder.The Elementary Equation of the Conjugate Transformation for Hexagonal Grid[J].Modeling in Computer Graphics,1993：21-42.

[44]Z J Zheng,A J Maeder.The Conjugate Classification of the Kernel Form of the Hexagonal Grid[J].Modern Geometric Computing for Visualization,1992：73-89.