混合扩频信号快速参数估计与识别算法✴

张佳芬，牟飞燕，雷翔

（电子科技大学成都学院，成都611731）

混合扩频信号快速参数估计与识别算法✴

张佳芬，牟飞燕，雷翔

（电子科技大学成都学院，成都611731）

针对混合扩频信号多是基于直接序列扩频和跳频扩频相结合的现状，提出了基于直接序列和线性调频相结合的混合扩频信号快速参数估计与识别算法。通过建立基于频域矩峰度系数的神经网络，将两类信号识别开来，信噪比为-2 dB时识别概率均达到95%以上。通过倒序共轭卷积和分段截取后快速解线调，实现了复合信号各参数的快速估计，信噪比为-1 dB时码速率估计精度均较高。

混合扩频；参数估计；调制识别；神经网络

1 引言

对复杂调制信号的参数估计与识别是通信及信息对抗的一个重要方面。混合扩谱通信系统近年来受到广泛关注。其中，由直接序列扩频（DSSS）和宽带线性调频（Chirp）相结合的混合扩频信号既同时具有两者的优点，又能弥补各自的不足，具有低截获和抗多普勒频移等优点［1-2］，被广泛应用于军事领域和民用通信中。研究该类型复合信号的参数估计与识别算法对民用通信及电子支援侦察具有重要意义。

对于混合扩频信号国内外已有不少文献提出各种参数估计与识别方法，但大多是围绕直接序列扩频和跳频扩频相结合的混合信号，对直接序列扩频和线性调频复合信号的研究又多是基于协作通信和部分先验信息已知的假设。文献［3］用动态聚类分析和高阶循环累积量估计跳频频率，计算量和存储空间较大。文献［4-6］引入了基于Wigner时频分布函数的伪码-载波调频复合信号的参数估计算法，由于要在时频平面进行二维搜索，算法较复杂且计算量较大。

本文基于BP神经网络实现了乘积型直接序列扩频／线性调频混合信号（以下简称乘积型混合信号）和卷积型直接序列扩频／线性调频混合信号（以下简称卷积型混合信号）的调制识别问题。针对卷积型混合信号，本文分别采用倒序共轭卷积法和快速解线调［7］法实现了混合信号码速率和调频参数的快速估计。仿真结果表明本文算法是有效可行的。

2 信号模型

式中，m（t）为直接序列扩频信号，uf（t）为线性调频

p定义Cp为码速率，则TpCp=1；P为m序列码长，N为m序列周期数，Tr为N=1时m序列的长度，Cl（Cl∈｛+1，-1｝）为m序列取值；f0为线性调频信号的起始频率，k为调制斜率，φ0为初始相位。

3 算法原理

3.1 信号识别

模式识别法是通过从信号中提取事先选取的特征进行调制类型分类的信号调制类型识别方法。这种方法虽然判决规则较复杂，但特征提取简单，易于计算。本文基于这种方法分别提取两种混合信号的频域矩峰度系数［10］，然后采用BP（Back Propagation）神经网络中的动量梯度下降法作为参数调整法，在0 dB信噪比下将频域矩峰度系数训练300次后保存，在线进行调制类型识别。算法流程如图1所示。

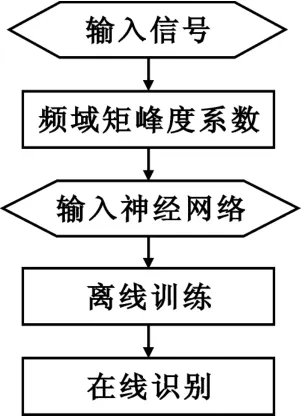
图1 基于神经网络的调制识别方法Fig.1 Modulation recognitionmethod based on neural network

仿真参数设置如下：TP=10μs，7位m序列为［-1，-1，1，-1，1，1，1］，B=1 MHz，fs=10 MHz，f0=0.5 MHz，SNR=-5～10 dB，每个信噪比下进行500次Monte Carlo实验，图2（a）和（b）分别为两种复合信号的识别概率。

图2 两种复合信号识别概率Fig.2 Identification probability of two kind of complex signals

由图2可见，当SNR≥-3 dB时，乘积型复合信号识别概率可以达到95%以上，而卷积型复合信号的识别概率则在SNR≥-2 dB时才能达到95%以上，这说明卷积型复合信号的矩峰度系数受噪声影响波动较大。

文献［11］通过分析两种复合信号的频域矩峰度系数的统计特性，设定门限将其识别开来。有些情况下门限的选取存在一定困难，本文提出的以神经网络算法作为参数调整法应用更普遍。

3.2 参数估计

3.2.1 算法概述

本文通过分析卷积型复合信号的频谱结构，推导出信号与其倒序共轭卷积后的第一个极值即为复合信号的码速率。求得信号码周期后，采用分段截取和快速解线调法实现了复合信号调频参数的快速估计。

假设接收机截获到的有用信号s（t）为

由式（4）知：

由式（3）得：

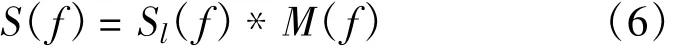
由傅里叶变换的性质知，若z（t）=x（t）⊗y*（-t）（y*（-t）代表y（t）的倒序共轭序列），则Z（f）=X（f）*Y*（f）。将信号与它自己的倒序共轭卷积，相当于求频域信号模的平方，则：

｜S（f）｜2=｜Sl（f）｜2*｜SP（f）｜2=

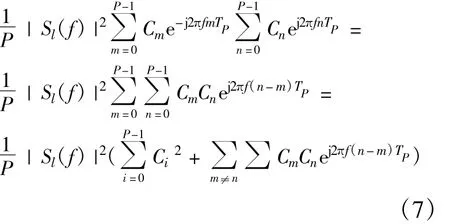
令n-m=k，则：

式中，x（k）为伪随机二相编码信号的非周期自相关函数，其表达式为

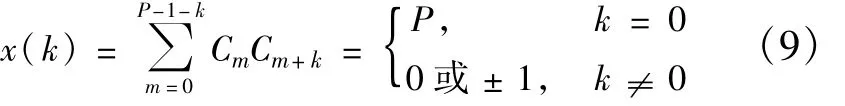
由文献［12］知，对于双极性码，非周期自相关函数x（k）的第一个值为-1或1，所以复合信号的频谱在码速率处出现一个极值，相应的时域函数在码周期处也呈现一个极值，搜索后即可求得信号的码周期。

3.2.2 性能仿真

仿真参数设置如下：f0=0.5MHz，k=1011Hz／s，TP=10μs，13位伪随机码为［-1-1-1-1 1 1 -1-1 1-1 1-1］，fs=10 MHz，SNR=-5～15 dB，每个信噪比下进行500次Monte Carlo试验，码速率估计的均方根误差曲线如图3所示。

图3 卷积型混合信号码速率估计归一化均方根误差Fig.3 Normalized RMSerror of all parametes of convolution signal

由图3可知，当信噪比大于-1 dB后，卷积型复合信号码速率估计的均方根误差均趋于稳定，且达到最低值。根据卷积型复合信号的产生机理，从原始信号开始或截止处以码周期为间隔截取一段信号，即为完整的线性调频信号，快速解线调［7］即可估计出复合信号的调频信息。故该算法有较高的参数估计精度且计算量较小，有利于实时处理。

本文算法与致谢部分提及文献中提出的算法（首先对信号向量按照子脉冲宽度进行窗口划分，计算其协方差矩阵，然后提取协方差矩阵两最大特征值对应特征向量，采用滑动窗技术实现子脉冲同步，最后利用快速解线性调频算法实现信号参数估计）相比，算法性能相近，但本算法对接收信号码元数和子脉冲长度没有过多要求，应用更广泛。

4 结论

基于信号的产生机理，本文提出了混合扩频信号的快速参数估计和识别算法。通过分析两种复合信号的频域矩峰度系数，引入BP神经网络中的动量梯度下降法作为参数调整法，实现了两种复合信号的识别；通过分析卷积型复合信号的频谱结构，采用倒序共轭卷积后快速解线调法实现了卷积性复合信号各参数的快速估计。

本文参数估计算法需先求解码速率而后实现调频参数的估计，求解有先后顺序，存在传递误差。后期工作将围绕这些方面展开深入研究，寻求更有效的参数估计方法。

5 致谢

本文在写作中，一些结论对比了电子科技大学博士研究生曾德国等同志在《线性调频-伪码卷积性复合信号参数估计方法》（已被《电子科技大学学报》录用，还未发表）一文中的结果，在此特表感谢。

［1］徐庆，徐继麟，周先敏，等.线性调频-二相编码雷达信号分析［J］.系统工程与电子技术，2000，22（2）：7-8. XUQing，XU Ji-lin，ZHOU Xian-min，et al.A Discussion of Performance of Hybrid Waveform of Radar［J］.Systems Engineering and Electronics，2000，22（2）：7-8.（in Chinese）

［2］孙洁.二相编码-线性调频信号的检测［J］.无线电通信技术，2003，29（2）：53-55. SUN Jie.The Detection of Hybrid Waveform Signal［J］.Radio Communications Technology，2003，29（2）：53-55.（in Chinese）

［3］郑文秀，赵国庆，罗明，等.混合SFH／DS扩频信号的跳频频率估计［J］.系统仿真学报，2008，20（7）：1852-1855. ZHENGWen-xiu，ZHAO Guo-qing，LUO Ming，et al. Hopping Frequencies Estimation of Hybrid SFH and DS Spread Spectrum Signals［J］.Journal of System Simulation，2008，20（7）：1852-1855.（in Chinese）

［4］GardnerW A，Spooner CM.Detection and source location of weak cyclostationary signals：simplifications of themaximum -likelihood receiver［J］.IEEE Transactions on Communications，1993，41（6）：905-916.

［5］林俊，熊刚，王智学.基于时频分析的伪码与线性调频复合体制侦察信号参数估计研究［J］.电子与信息学报，2006，28（6）：1045-1048. LIN Jun，XIONGGang，WANG Zhi-xue.Study on Reconnaissance Signal Parameter Evaluation of PN and LFM Based on Time-Frequency Analysis［J］.Journal of Electronics＆Information Technology，2006，28（6）：1045-1048.（in Chinese）

［6］熊刚，杨小牛，赵惠昌.基于平滑伪Wigner分布的伪码与线性调频复合侦察信号参数估计［J］.电子与信息学报，2008，30（9）：2115-2119. XIONG Gang，YANG Xiao-niu，ZHAO Hui-chang.Parameter Estimation of Reconnaissance Signal Combined PN and LFM Based on Smoothed Pseudo Wigner Distribution.［J］.Journal of Electronics＆Information Technology，2008，30（9）：2115-2119.（in Chinese）

［7］刘渝.快速解线性调频技术［J］.数据采集与处理，1999，14（2）：175-178. LIU Yu.Fast Dechirp Algorithm［J］.Journal of Data Acquisition＆Processing，1999，14（2）：175-178.（in Chinese）

［8］张佳芬，和小东，唐斌.伪码-线性调频信号快速参数估计算法［J］.电讯技术，2009，49（12）：100-104. ZHANG Jia-fen，HE Xiao-dong，TANG Bin.A Fast Parameter Estimation Approach of Multiplicative Signal Combined PRBC and LFM［J］.Telecommunication Engineering，2009，49（12）：100-104.（in Chinese）

［9］殷国平，曹旭平，崔占忠.伪码调相与线性调频复合调制信号探测性能研究［J］.弹箭与制导学报，2007，27（2），280-282. YINGuo-ping，CAO Xu-ping，CUIZhan-zhong.Research on Detection Performance of Complex Modulation Signal Using Pseudorandom Code Phase Modulation and Linear Frequency Modulation［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2007，27（2）：280-282.（in Chinese）

［10］范伟.雷达有源干扰信号特征分析与识别算法研究［D］.成都：电子科技大学，2007. FANWei.The feature extraction and identification algorithm of active jamming［D］.Chengdu：University of Electronic Science and Technology of China，2007.（in Chinese）

［11］吕远.复杂调制雷达信号的调制识别与参数估计算法研究［D］.成都：电子科技大学，2009. LV Yuan.Recognition and Parameter Estimation for Complex Modulated Radar Signals［D］.Chengdu：University of Electronic Science and Technology of China，2009.（in Chinese）

［12］张明友，汪学刚.雷达系统［M］.2版.北京：电子工业出版社，2006. ZHANG Ming-you，WANG Xue-gang.Radar system［M］.2nd ed.Beijing：Publishing House of Electronic Industry，2006.（in Chinese）

ZHANG Jia-fen was born in Yanzhou，Shandong Province，in 1984.She received the M.S.degree in 2009.She is now a teaching assistant.Her rearch direction is digital signal processing.

Email：prettyjiafen＠163.com

牟飞燕，女，硕士，助教，主要研究方向为电路与系统。

MOU Fei-yan is now a teaching assistantwith the M.S.degree.Her rearch direction is circuits and systems.

Fast Parameter Estimation and Recognition Approach for Hybrid Spread Spectrum Signals

ZHANG Jia-fen，MOU Fei-yan，LEIXiang
（Chengdu College，University of Electronic Science and Technology of China，Chengdu 611731，China）

To improve the status of hybrid spread spectrum signalmainly based on direct sequence spread spectrum（DSSS）signal and frequency hopping（FH）spread spectrum signal，a fast approach is presented for DSSS and chirp spread spectrum.By establishing coefficient of frequency domainmoment peak based neural network，two types of signals are identified.The recognition probability is above 95%when SNR（Signal-to-Noise Ratio）is close to-3 dB.By reverse-order conjugation convolution-fast dechirp，the code rate and initial frequency and slope of convolutional compound signal can be estimated.Code rate estimation accuracy is higher when SNR is close to-1 dB.

hybrid spread spectrum；parameter estimation；modulation recognition；neural network

The Science and Technology Foundation of Chengdu College ofUniversity of Electronic Science and Technology of China

TN971.1

A

10.3969／j.issn.1001-893x.2011.09.014

张佳芬（1984—），女，山东兖州人，2009年获工学硕士学位，现为助教，主要研究方向为数字信号处理；

1001-893X（2011）09-0069-04

2011-04-14；

2011-06-10

电子科技大学成都学院科技基金项目