计及分布式电源和负荷静态特性的最优低频减载*

刘志鹏 文福拴 Gerard Ledwich

(1.华南理工大学电力学院，广东广州510640;2.浙江大学电气工程学院，浙江 杭州310027;3.昆士兰科技大学工程系统系，澳大利亚布里斯班4001)

低频运行对电力系统安全稳定和电力用户的生产和生活都存在巨大威胁.例如，当频率低于额定值时，汽轮发电机的叶片震动会变大或可能产生共振而断裂，从而导致汽轮发电机退出运行，使频率进一步恶化.对于电力用户而言，频率变化会引起加工工业产品所使用的异步电动机转速不稳定，从而影响产品质量，甚至出现次品和废品.此外，频率波动还会影响一些电子设备的准确性和可靠性，甚至导致某些设备无法正常工作.

一般而言，低频减载是当电力系统发生严重频率下降事故时防止频率崩溃所能够采取的最后一项补救措施，直接关系到电力系统遇到大扰动或者大功率缺额时，通过切除部分负荷来维持系统功率平衡和保持频率稳定的能力.

到目前为止，国内外已有不少学者对低频减载策略做了研究.文献［1］中提出了基于轨迹量化分析和风险控制的关于低频减载和低压减载相互优化协调的发展方向，并采用安全裕度对控制措施的性价比来指导搜索和迭代优化.文献［2］中提出了一种计及负荷频率特性的低频减载方案，优先切除频率调节系数小的线路，从而有利于系统频率的快速恢复和系统稳定.文献［3］中基于非递归牛顿型算法估计频率和频率变化率，提出了一种能够防止电力系统频率崩溃和动态不稳定的低频减载策略.针对多台发电机发生事故而退出运行的情况，文献［4］中提出了自适应方法和系统备用容量控制相结合的低频减载策略.此外，文献［5-7］中将低频减载策略描述为非线性规划问题，并采用遗传算法、粒子群法等优化方法求解.这类方法虽然能够优化需要切除的负荷量，减少经济损失，但是往往需要较长的计算时间，因而很难满足快速性要求.综上所述，目前的低频减载策略在切除的负荷量、切除顺序和有功功率缺额的确定方面，仍然有不少问题值得研究.

现代电力系统规模的增大和复杂性的增加，以及分布式电源在系统中的数量和所占容量比重的增大，都对形成适当的低频减载策略带来了新的挑战，引入了新的问题，例如在确定低频减载策略时应如何避免在切除负荷时可能导致的分布式电源孤岛运行、应该如何利用分布式电源来尽量减少甚至避免切除负荷等.但到目前为止，还没有这方面的研究报道.在此背景下，文中对计及分布式电源和负荷静态特性的最优低频减载策略问题进行深入研究.

1 最优低频减载策略架构

这里所提出的最优低频减载策略的核心思想是采用“基本轮”和“特殊轮”这两个过程.具体地讲，基本轮以系统频率和频率变化率为动作信号，根据系统中等值发电机的摇摆方程和此时系统的旋转备用容量，迅速计算出每轮需要切除的负荷量，然后根据每轮切除负荷顺序依次切除负荷，最终使得系统快速摆脱紧急状态.

在基本轮切除部分负荷后，系统频率虽然摆脱了紧急状态，但此时可能处于低频范围内的波动状态或悬浮于某一低频值.为保证频率尽快恢复到安全状态，提出再执行具有优化功能的特殊轮，通过合理优化分布式电源的出力和调整部分负荷以减少需要切除的负荷量和满足系统安全运行要求.

需要指出，文中提出的低频减载策略是在假设配电管理系统已经完备的基础上发展的，因此，系统中旋转备用的实时采集、特殊轮在执行时所需的全网信息和低频减载装置的远程控制以及保护值的远方调整等都可以通过配电管理系统来实现.

1.1 基本轮简介

基本轮的目标是在保证不过多切除负荷的情况下，尽快阻止频率下降，避免系统频率崩溃.

基本轮的主要参数和设置原则如下:

(1)延时

为防止系统振荡或电压大幅度变化引起基本轮误动作，需要设定一个延时tD1，其值一般取为0.2～0.3s［1］.

(2)启动信号

当系统的频率变化率小于零并且频率f小于或等于基本轮的首轮动作频率(f≤fd1)时，基本轮开始实施.

(3)首轮动作频率

对于首轮动作频率的设置，需要从两个方面来协调考虑:一是要有利于抑制当系统出现严重功率缺额时所导致的频率大幅下降，所以首轮动作频率的设定值不宜过高;二是要有利于充分利用系统旋转备用容量来尽量避免切负荷，并将频率恢复到安全值，所以首轮动作频率的设定值也不能过低.综合考虑以上两点后，可给定首轮动作频率fd1=49.2Hz.

(4)末轮动作频率

末轮动作频率不能低于机组的低频保护值，同时还要留有0.3～0.5 Hz左右的裕度［8］.因此，给定末轮动作频率为基本轮的轮数.

(5)频率级差

在基本轮中，将动作频率分成高频率和低频率两个区段.动作频率在每个区段内等距分级.在高频率区段内，频率级差设置稍小，以抑制频率下降;在低频率区段内，频率级差略大，以减少过切［8］.具体来讲，第i轮频率级差(单位为Hz)为

根据首轮动作频率、末轮动作频率和每轮频率级差，可得到基本轮的最多轮数NmaxR=6.

(6)轮数

基本轮的轮数满足以下条件:

上述方法是以低频减载的传统方法和自适应方法为基础设计出来的，综合了二者的优点.传统方法速度快，但是每轮切除的负荷量是固定的，因而容易过切;另一方面，自适应方法的优点是利用频率变化率测量值可以较为准确地计算出切除负荷量，以避免过切，缺点是容易产生频率长时间处于低频范围内的波动状态或悬浮在某一低频值，且其中所采用的简化频率响应模型没有考虑负荷影响.

1.2 特殊轮简介

分布式电源对制定低频减载策略会产生影响.基于此，文中将优化分布式电源出力和调整部分负荷相结合的方法引入到特殊轮中，以避免频率长时间处于低频范围内的波动状态或悬浮在某一低频值，从而有助于系统尽快恢复到正常运行状态.特殊轮的主要参数和设置原则如下.

(1)延时

在基本轮中切除部分负荷后，频率会在一段时间内处于波动状态.为了限制频率波动范围以便判断频率变化率的方向和减少频率优化搜索范围，需要设定一个延时tD2，其设定值可通过仿真或实验确定(例如，可以给定其为1.0s).

(2)启动信号

在经过基本轮和延时tD2后，当系统的频率变化率大于零且频率大于基本轮首轮动作频率时，特殊轮开始实施.

(3)结束频率

(4)轮数

根据优化后的计算结果，在特殊轮中，直接调度优化确定分布式电源的出力，并在必要时切除部分负荷.即特殊轮的轮数NR=1.

上述特殊轮是类比基本轮设计出来的，基于两点考虑:(1)解决频率长时间处于低频范围内的波动状态或悬浮在某一低频值的问题;(2)通过采用适当的优化方法来发挥分布式电源的作用.从本质上讲，基本轮和特殊轮相当于低频减载策略的粗调和细调.

2 基本轮的数学模型

2.1 K 值的确定

负荷功率一般会随系统电压和频率而变化，这就是所谓的负荷电压和频率特性.文中采用如下的负荷静态特性形式:

式中:VL为负荷所在节点电压;为额定电压;Δ f为系统频率变化量;PL、QL分别为负荷的有功功率和无功功率;和分别为负荷的额定有功和无功功率;Kpf和Kqf分别为负荷有功和无功功率的频率调节效应系数，取值范围分别为［0.0，3.0］和［－2.0，0.0］［9］;式中的各系数应满足 ap+bp+cp=1和aq+bq+cq=1.

在同时考虑负荷的频率和电压特性后，单位频率变化引起的各节点处负荷的有功功率变化量(简称为K值)为

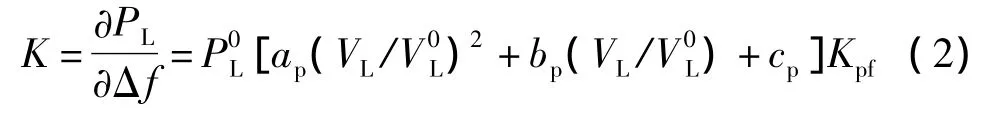
由上式可知，当频率下降时，K值大的负荷有功功率会下降更多.如果所采用的低频减载策略可以保证系统中剩余负荷的K值尽可能大一些，不但有利于减少系统有功功率缺额，也有助于抑制频率下降和恢复功率平衡.因此，可以把负荷的K值按从小到大顺序作为基本轮中每轮切除负荷的顺序.

2.2 负荷切除量的计算

发电机组i的摇摆方程可表示为

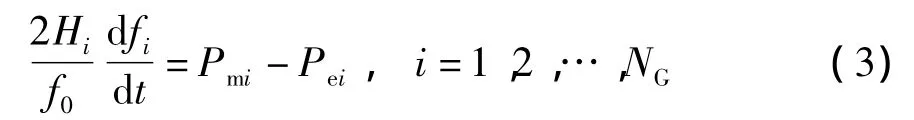
式中，Hi、Pmi、Pei和 fi分别为机组 i的惯性时间常数、机械功率、电磁功率和频率，NG为发电机组的台数，f0为额定频率.

对于包括NG台发电机组的系统，当频率发生变化后，系统的有功功率缺额为

将式(4)整理可得

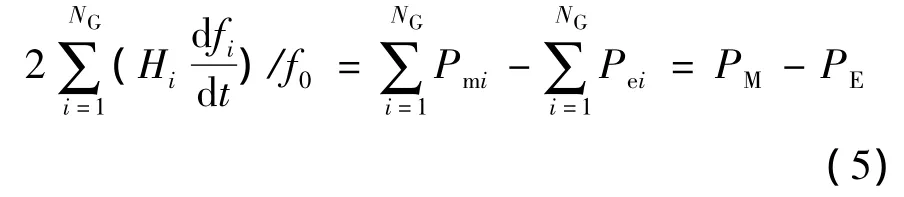
式中:PM为总机械功率为总电磁功率

将式(5)左边进一步化简，可得

从而，等值发电机的摇摆方程为

式中:ΔP为系统有功功率不平衡量，ΔPS=PM－PE.

为了使系统有功功率尽快恢复到平衡状态，必须消除有功功率缺额.同时，考虑到系统中一般都有一定的旋转备用容量［10］，因此切除的负荷量应为

式中，ε为修正系数(可以给定为1.05)，PSR为系统旋转备用容量.频率变化率在频率下降未得到有效抑制之前是趋于增大的，这会导致按照其测量值计算出的切除负荷量比实际值小，所以此处添加一个修正系数.

2.3 切除负荷的原则及顺序

当频率严重下降导致系统出现紧急情况时，有时只有切除部分负荷才能保证系统正常运行.切除负荷必须按照事先制定的原则来执行，否则不但损失了负荷，而且可能加剧系统的崩溃.因此，在基本轮中制定每轮切除负荷的原则如下:

(1)按照负荷的重要性，将其分为n个类型，记作 L=i(i=1，2，…，n).L 的值越小，负荷的重要性越低，其在被切除的顺序中越靠前.

(2)在同类负荷中按照K值从小到大的顺序，将负荷进行排序.负荷的K值越小，其被切除的顺序越靠前.

根据上述原则，各类负荷的K值排列顺序为

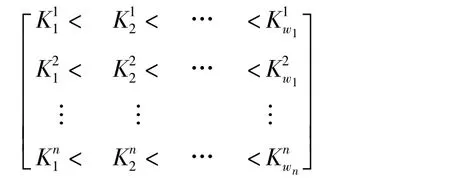
其中，下标wi(i=1，2，…，n)表示第L=i类负荷中所包含的负荷数.

基本轮中每轮切除负荷的具体步骤如下.

(1)设置负荷类型计数器i=1.

(2)在第L=i类负荷中，根据K值从小到大的顺序依次切除负荷，在确定所需切除的负荷量的过程中需要判断累计切除的负荷量是否小于或等于本轮需要切除的负荷量.如果切除量达到本轮需要切除的负荷量，则本轮切除负荷结束;否则，继续在这类负荷中安排切除，如果这类负荷切除完毕后仍未达到本轮需要切除的负荷量，则转下步.

(3)置i=i+1，然后返回步骤(2).

3 特殊轮的数学模型

3.1 目标函数

以切负荷成本最小、节点电压质量指标最优、网损最小3项指标的组合为特殊轮的目标函数:

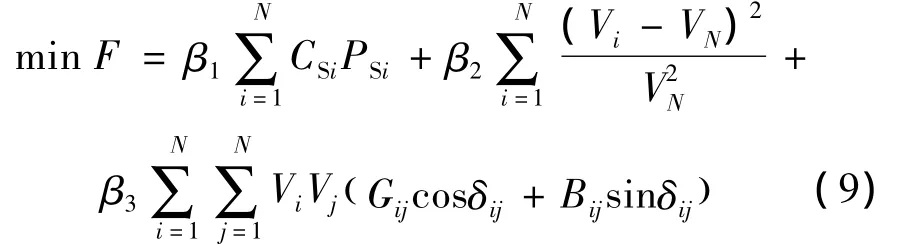
式中:N为配电系统中的节点数，并假设平衡节点的编号为N;β1、β2和β3均为权重系数且满足 β1+β2+β3=1，文中采用层次分析法来确定这些权重系数;CSi为节点i处切除负荷的成本系数，越重要的负荷其值越大;PSi为节点i处切除的负荷有功功率，如该节点处未切除负荷，则PSi=0;VN为平衡节点的电压幅值;Vi和Vj分别为节点i和j的电压幅值;Gij和Bij分别为支路ij的电导和电纳;δij为节点i和节点j之间的电压相角差.

3.2 等式约束

在特殊轮的执行过程中，各节点需要满足如下潮流约束:

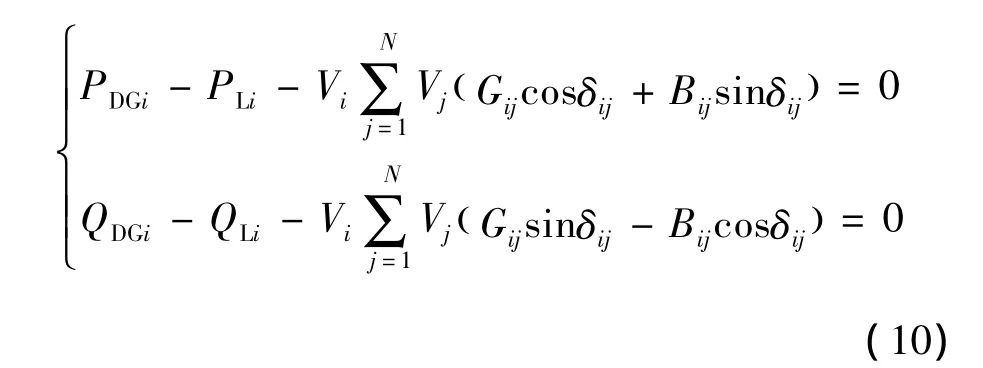
式中:PDGi和QDGi分别为节点i处分布式电源的有功和无功功率;PLi和QLi分别为节点i处负荷的有功和无功功率为额定频率下支路ij的电纳，Bij考虑了线路电纳的依频特性［11］.

3.3 不等式约束

在特殊轮的数学模型中所考虑的不等式约束主要包括

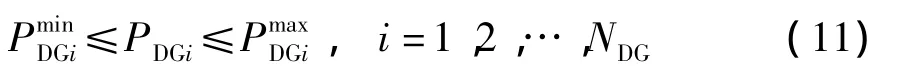
式中，NDG为分布式电源的数目.

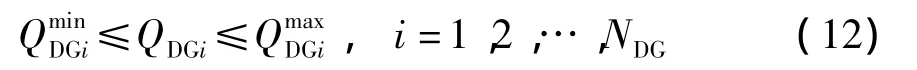
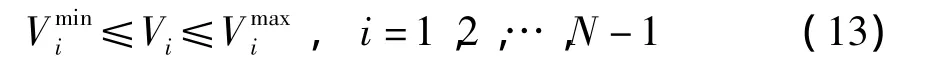
(4)馈线最大电流约束(即Iijmax):

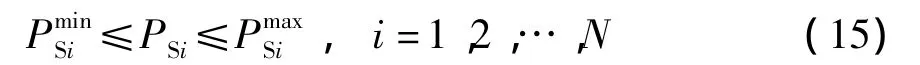
(6)在切除部分负荷后，频率需要达到的安全区间约束(即在上下限和之间):

(7)在切除部分负荷的前后，各节点处负荷的功率因数保持不变，其数学模型如下:

式中，QSi为节点i处切除的负荷无功功率.

综上所述，这里所构造的计及分布式电源和负荷静态特性的特殊轮的数学模型可概括为

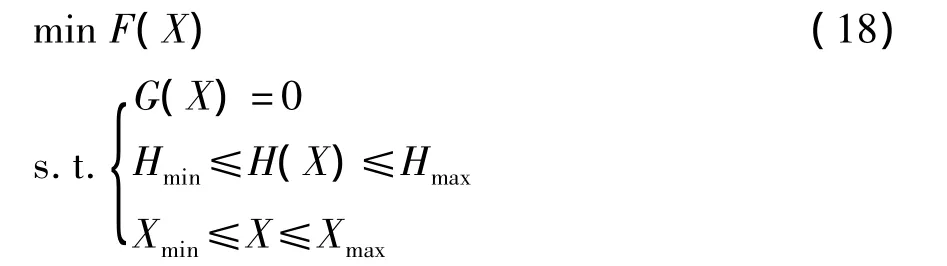
式中，F(X)、G(X)和H(X)分别为目标函数、等式约束和不等式约束，Hmax和Hmin分别为H(X)的最大和最小值，X为状态变量，Xmax和Xmin分别为X的最大和最小值.

需要指出，上面所构造的模型框架同样可以容纳其它约束条件.式(18)表示了一个非线性规划问题，文中采用文献［12］中改进的原对偶内点法来求解.因篇幅所限，这里不赘述.

为了保证能够得到最优解，在改进的原对偶内点法的收敛条件中设定了优化指标OT，该指标需要满足的条件如下:

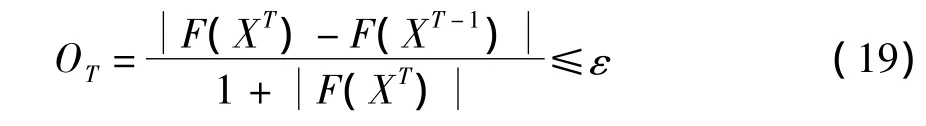
式中，ε为常数，T为迭代次数.

4 算例分析

以改进的IEEE 37节点配电系统为例说明所提出的最优低频减载策略.在节点703、704、705和734处接入了4台分布式电源，如图1所示.4台分布式电源的具体参数见表1.该系统通过节点799与变电站相连接，因而此处可以用一台等值发电机表示并假设其惯性时间常数为0.8 s.负荷参数见表2.

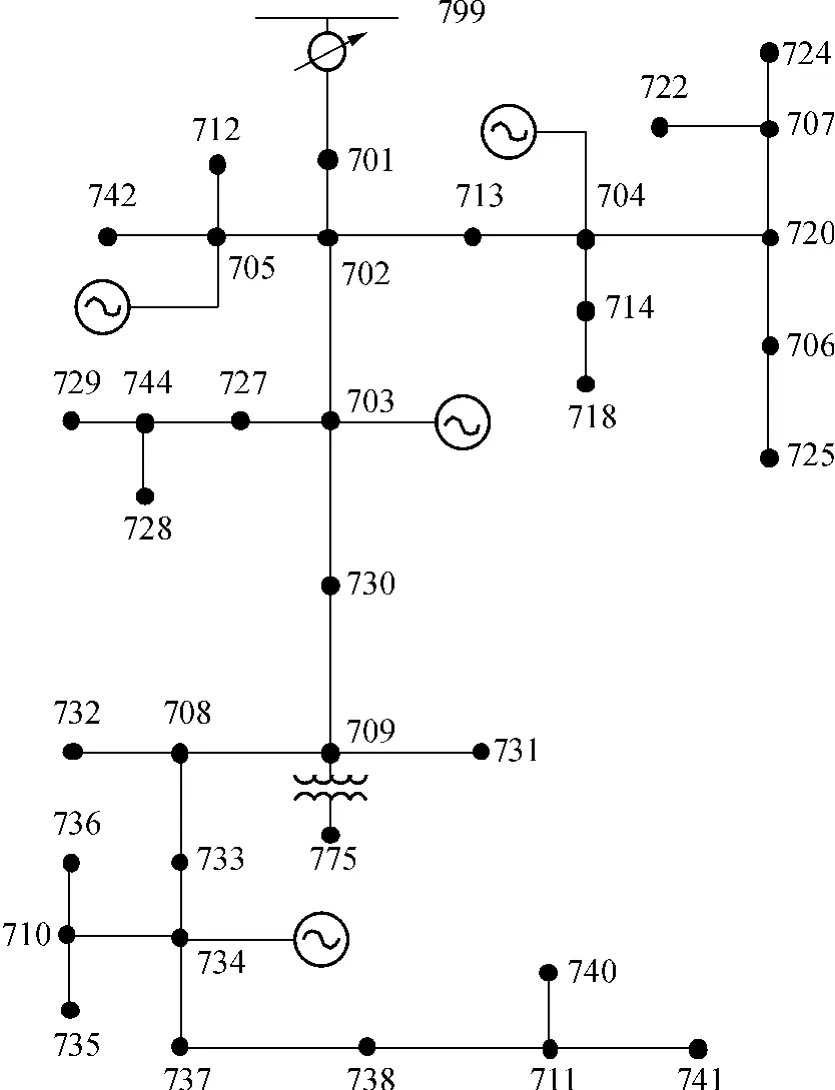
图1 IEEE 37节点配电系统Fig.1 IEEE 37-node test feeder

假设在节点799处安装的可调变压器组中有一台因故障退出运行，导致从此处输入配电系统的有功功率减少了200kW，其占整个配电系统总有功功率的22.33%.当检测到频率变化率小于0且经过延时tD1后，所提出的最优低频减载策略开始执行.整个执行过程中的频率变化情况如图2所示.

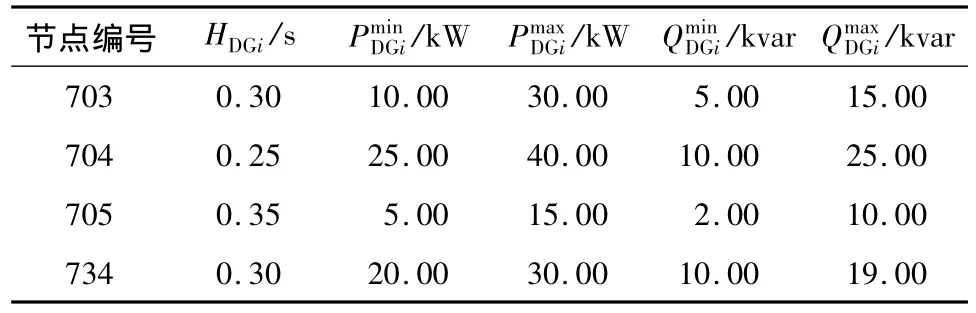
表1 接入的分布式电源的参数Table 1 Parameters of penetrated distributed generators

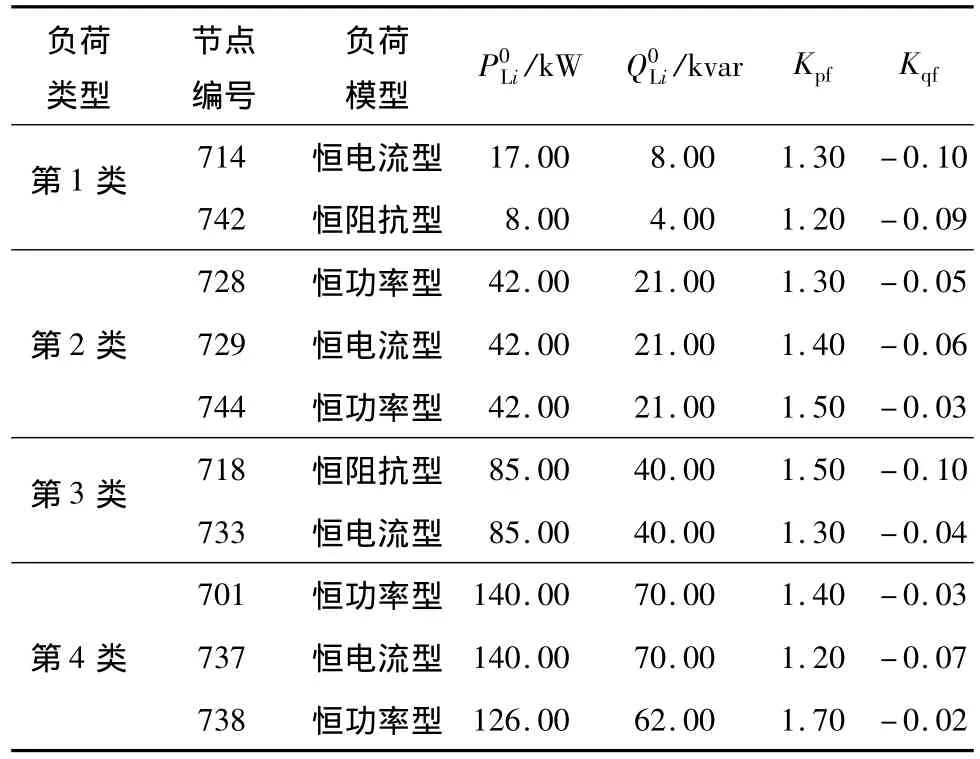
表2 初始负荷Table 2 Original loads

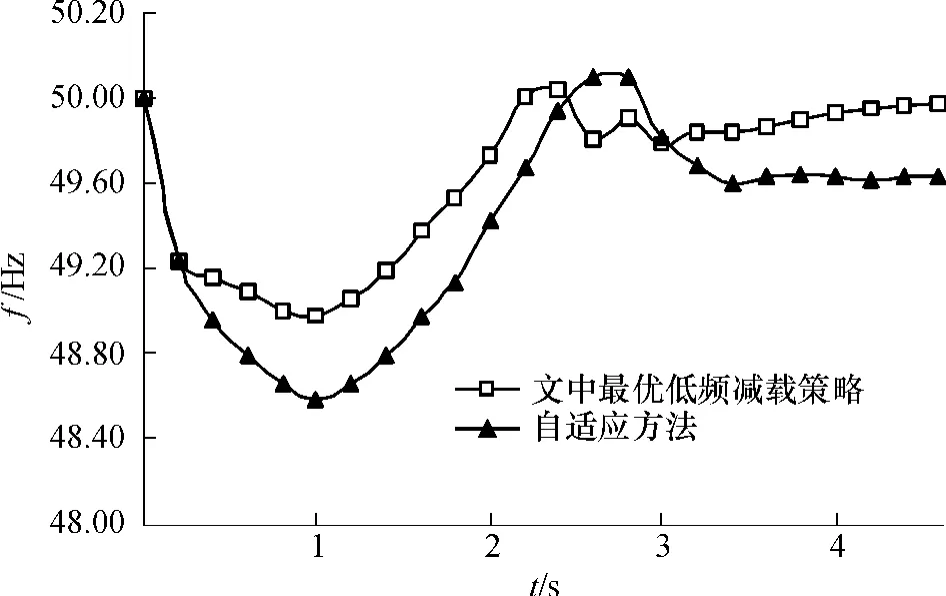
图2 文中最优低频减载策略和自适应方法执行过程中的频率变化Fig.2 Frequency variations in execution procedures of proposed optimal under-frequency load shedding and the adaptive approaches

由图2可看出，与自适应方法相比，在基本轮中，通过快速切除部分负荷抑制了频率下降;而在特殊轮中，通过优化分布式电源的出力和调整部分负荷，避免了频率长时间处于低频范围内的波动状态或悬浮在某一低频值.在基本轮中每轮切除负荷的方案如表3所示.在特殊轮执行后，各节点处的负荷变化如表4所示.从表2－4中可以看出，基本轮中切除的负荷量较特殊轮要大一些.在改进的原对偶内点法迭代过程中，优化指标是趋向于0的，如图3所示.表5和6分别给出了特殊轮执行前后分布式电源的出力和式(12)所表示的目标函数中各指标值的变化，其中表6内的切负荷成本是采用文献［13］中介绍的停电1 h以内的停电损失费用计算的.可以看出，通过对分布式电源出力的优化调整减少了需要切除的负荷量，同时频率和电压等参数得以改善.这进一步表明了特殊轮执行后的优化效果.

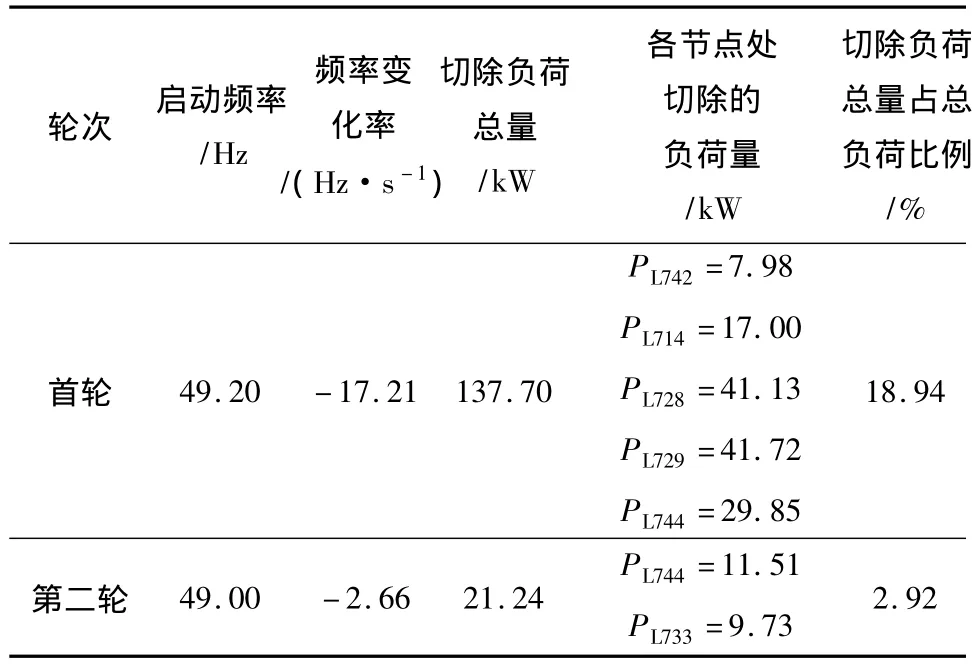
表3 基本轮中每轮切除负荷的方案Table 3 Load shedding schemes in each iteration of basic round

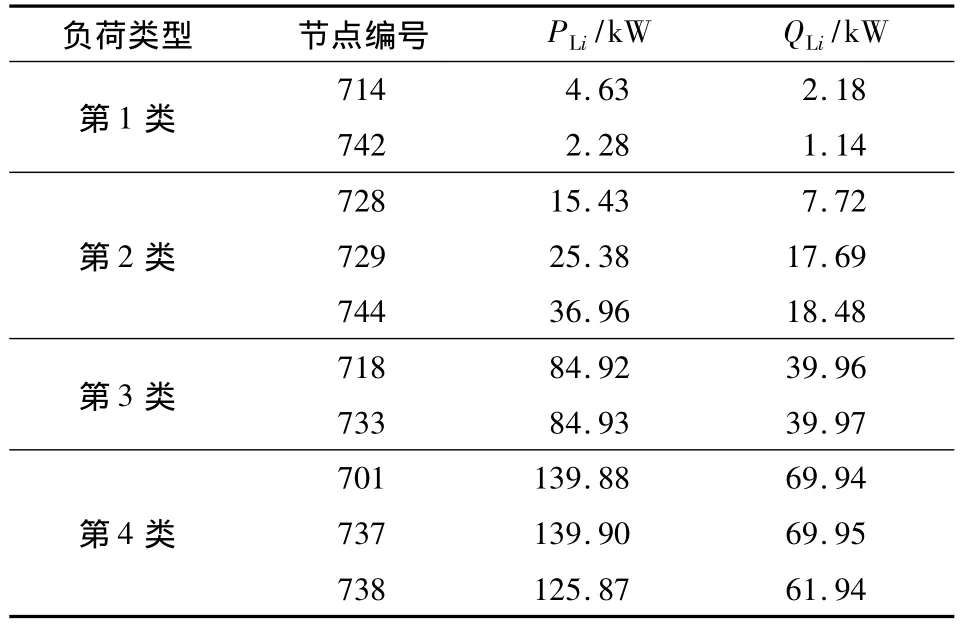
表4 特殊轮执行后的负荷情况Table 4 Loads after executing special round

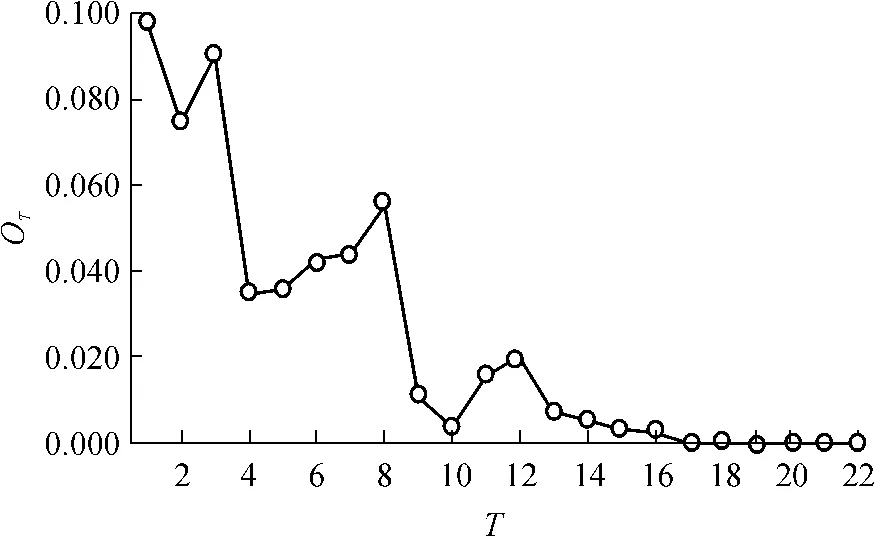
图3 在改进的原对偶内点法迭代过程中优化指标的变化Fig.3 Variations of optimal index in the iteration of the modified primal-dual interior point algorithm

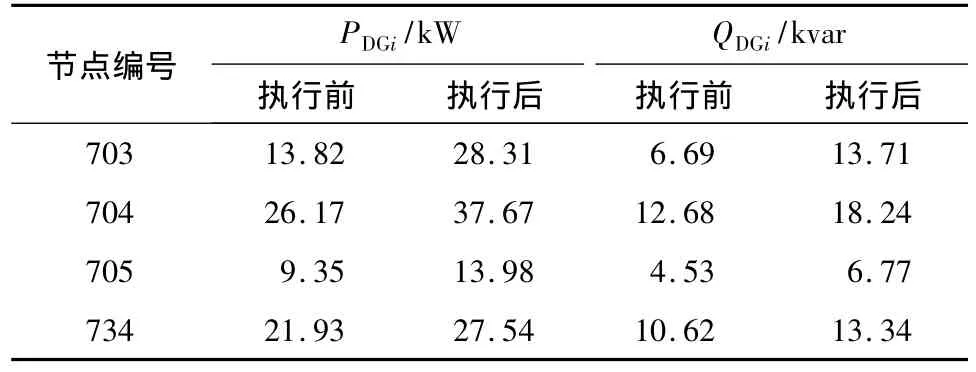
表5 特殊轮执行前后分布式电源的出力变化Table 5 Output power variations of DGs before and after execution of special round

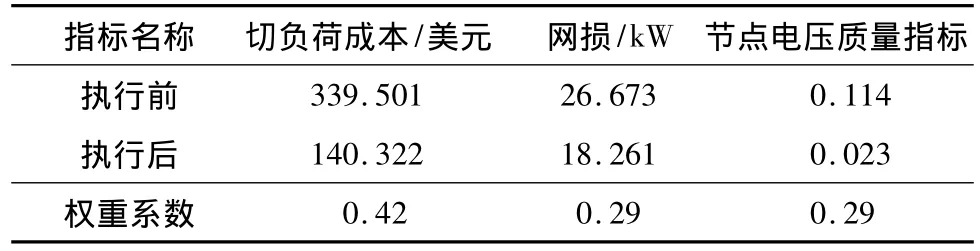
表6 特殊轮执行前后目标函数中的各项指标值Table 6 Values of all indices of objective function before and after execution of special round

5 结论

在分布式发电快速发展的背景下，文中提出了计及分布式电源和负荷静态特性的最优低频减载策略.该策略以频率及其变化率为执行依据，并由基本轮和特殊轮组成.文中对基本轮和特殊轮的基本设置、执行流程和数学模型等做了系统的研究和阐述.最后，用改进的IEEE 37节点配电系统为例，说明了所提出的最优低频减载策略的基本特征:基本轮能够保证频率摆脱紧急状态，特殊轮能够保证频率恢复到安全状态并使系统运行参数最优.

在低频减载策略执行过程中，除了文中提到的频率变化率测量误差外，还可能会受到一些不确定性因素的影响.为此，文中将能够发挥粗调和细调作用的基本轮和特殊轮相结合，以达到尽量降低这些因素对低频减载策略正确执行可能带来的风险.

［1］薛禹胜，任先成，Wu Q H，等.关于低频低压切负荷决策优化协调的评述［J］.电力系统自动化，2009，33(9):100-107.Xue Yu-sheng，Ren Xian-cheng，Wu Q H，et al.A review on optimization and coordination of under frequency/voltage load shedding［J］.Automation of Electric Power Systems，2009，33(9):100-107.

［2］熊小伏，周永忠，周家启.计及负荷频率特性的低频减载方案研究［J］.中国电机工程学报，2005，25(19):48-51.Xiong Xiao-fu，Zhou Yong-zhong，Zhou Jia-qi.Study of under frequency load shedding scheme based on load frequency characteristics［J］.Proceedings of the CSEE，2005，25(19):48-51.

［3］Terzija V V，Koglin H J.Adaptive underfrequency load shedding integrated with a frequency estimation numerical algorithm ［J］.IEE Proceedings:Generation，Transmission and Distribution，2002，149(6):713-718.

［4］Chuvychin V N，Gurov N S，Venkata S S，et al.An adaptive approach to load shedding and spinning reserve control during underfrequency conditions［J］.IEEE Transactions on Power Systems，1996，11(4):1805-1810.

［5］Palaniswamy K A，Sharma J，Misra K B.Optimum load shedding taking into account of voltage and frequency characteristics of loads［J］.IEEE Transactions on Power Apparatus and Systems，1985，104(6):1342-1348.

［6］Sanaye-Pasand M，Davarpanah M.A new adaptive multidimensioanal load shedding scheme using genetic algorithm［C］∥Proceedings of 2005 Canadian Conference on Electrical and Computer Engineering.Saskatoon:［s.n.］，2005:174-1977.

［7］Nakawiro W，Erlich I.Optimal load shedding for voltage stability enhancement by ant colony optimization［C］∥Proceedings of 15th International Conference on Intelligent System Applications to Power Systems.Curitiba:［s.n.］，2009:1-6.

［8］DL 428—91.电力系统自动低频减负荷技术规定［S］.北京:中国电力出版社，1991.

［9］Concordia C，Ihara S.Load representation in power system stability studies［J］.IEEE Transactions on Power Apparatus and Systems，1982，101(4):969-977.

［10］Seyedi H，Sanaye-Pasand M.New centralised adaptive load-shedding algorithmsto mitigate powersystem blackouts［J］.IET Generation，Transmission ＆ Distribution，2009，3(1):99-114.

［11］Arini E M.Optimal dynamic load shedding policy for generation load imbalances including characteristics of loads［J］.International Journal of Energy Research，1999，23(1):79-89.

［12］Liu Zhi-peng，Wen Fu-shuan，Ledwich G，et al.Optimal sitting and sizing of distributed generators based on a modified primal-dual interior point algorithm［C］∥Proceedings of 2011 4th InternationalConference on Electric Utility Deregulation and Restructuring and Power Technologies(DRPT).Weihai:［s.n.］，2010:1360-1365.

［13］Billinton R，Wang Peng.Distribution system reliability cost/worth analysis using analytical and sequential simulation techniques［J］.IEEE Transactions on Power Systems，1998，13(4):1245-1250.