二维Gabor滤波器组的设计及虹膜识别的实现

林 喜，林喜荣，戴晓清

(1.清华大学 深圳研究生院，广东 深圳 518055;2.清华大学 精密测试技术及仪器国家重点实验室，北京 100084)

0 引言

虹膜识别是一种利用人眼虹膜纹理信息自动鉴别身份的技术，具有识别精度高、速度快和稳定性好等优点。Daugman［1］提出二维Gabor小波变换的虹膜纹理相位编码方法，不同虹膜之间的匹配程度用特征向量间的海明距离度量。Wildes［2］使用Laplacian金字塔多分辨力技术计算相关系数，使用Fisher线性准则对特征模式进行分类。Boles等［3］使用小波变换过零点理论提取虹膜信息特征，通过统计过零点表达在不同采样点的欧式距离之和进行模式匹配。Ma等［4］用二次样条小波的模极值点来检测虹膜图像的局部变化点，对位置量进行二值编码，使用海明距离进行匹配。

1 图像预处理

设采集设备拍摄到的图像除包括虹膜纹理区域外，还有其他很多不相关的部位，如眼睑、睫毛、瞳孔和巩膜等。光照强度的变化引起瞳孔张缩也会引起虹膜纹理的非线性形变。光斑反射也会对虹膜纹理造成破坏。图像的预处理用于消除这些因素对识别结果产生的影响，包括图像去噪、虹膜分割、形变校正、眼睑和睫毛检测，归一化及增强处理［5－6］。预处理的结果如图1 所示。

图1 图像预处理

2 二维Gabor滤波器组的设计

虹膜纹理由许多互相交错的斑点、细丝、冠状、条纹、隐窝等细微特征组成。这些特征在归一化之后表现为不同频率和方向的纹理。二维Gabor小波变换［7］在理论上能够获得二维空域和二维频域的最佳联合分辨率，具有不同空间频率带宽、空间尺度和方向的滤波器组特别适合用于虹膜纹理的特征提取。

2.1 二维Gabor滤波器

Gaobr函数是由椭圆高斯函数与三角函数进行调制的结果，得到偶对称的实部和奇对称的虚部。基于直角坐标系的二维Gabor函数定义为

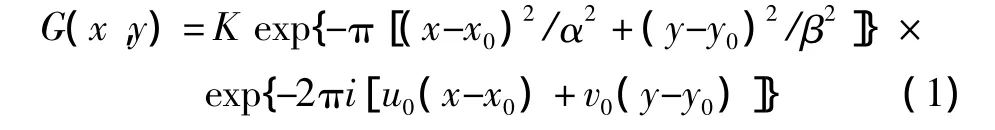
式中:(x0，y0)为滤波器的中心，此处坐标取值为(0，0)，即每个子滤波器的中心对应为每个子图像块的中心;α和β分别为滤波器的宽度和高;K为非零的实数，在本文中对特征编码没有影响，取值为1。二维Gabor滤波器的傅里叶变化形式为

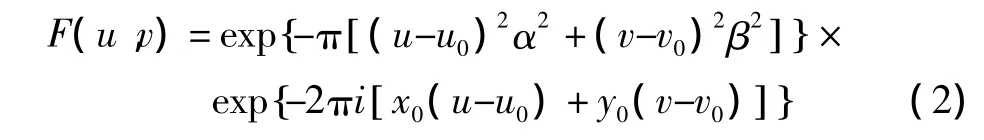
2.2 滤波器组参数的设计

在进行特征编码时，首先将归一化之后的图像划分为与滤波器大小相等的子图像块。滤波器的中心确定与每个子图像块的中心重合。

2.2.1 频率参数设计

不同频率的滤波器能够提取到疏密程度不同的虹膜纹理特征。大频率值的滤波器适合提取较密纹理的变化信息，小频率值的滤波器适合提取稀疏纹理的结构信息。

可分性指标(Discriminating Index，DI)可用来衡量虹膜识别算法的综合性能，公式为

式中:m1和为类内海明距离的统计均值和方差，m2和为类间海明距离的统计均值和方差。选用一组固定的滤波器角度参数，以f=1/ω为横坐标，可分性指数DI为纵坐标，关系曲线具有明显的单峰值(如图2所示)，根据牛顿法可以求得曲线的最大值和对应的横坐标1/ω0。设f0为最接近1/ω0的整数，以f0为中心，按一定的步长选择合适组数的频率，作为二维Gabor频率参数设计的依据。例如曲线对应可分性指标最大值的f0=20，选取f0－2，f0和f0+2可作为Gabor滤波器的一个频率参数组。

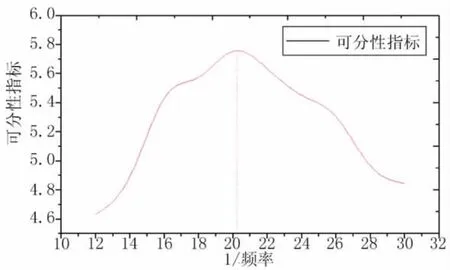
图2 频率与可分性指标关系实验拟合曲线

2.2.2 角度参数设计

归一化图像在不同方向上所包含的虹膜纹理信息量差异较大。纹理信息在某一角度方向的集中程度与归一化图像的大小和长宽比例相关。

先锋遗传算法［8－9］(Vanguard Genetic Algorithm)根据种群的进化情况而自适应调整交叉概率和变异概率，特别适合多峰值函数的优化问题。固定一组频率参数，可分性指标与滤波器角度之间符合双峰值的曲线关系(如图3所示)，在2个峰值角度范围内，可分性值较高，且稳定性好，表明此角度区间的虹膜纹理特征较为丰富。

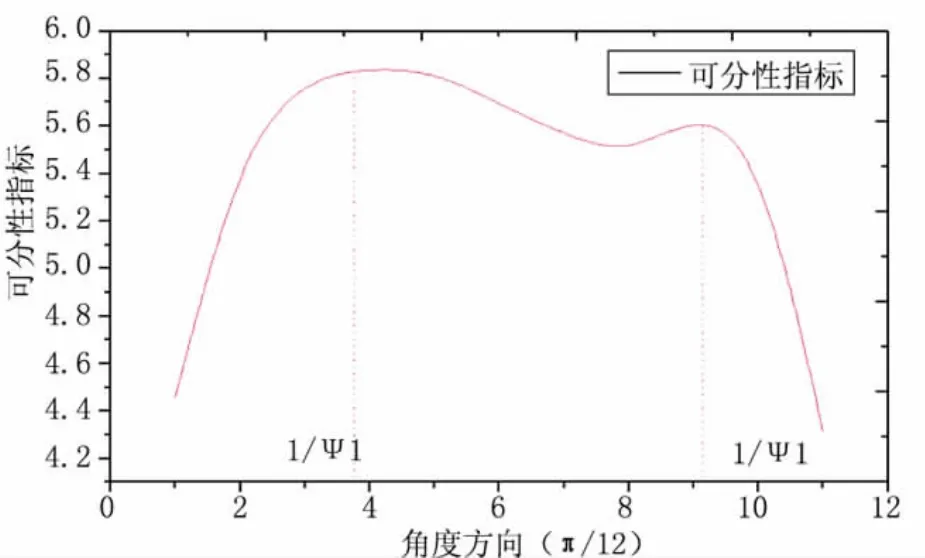
图3 滤波器角度与可分性指标的关系曲线

2.2.3 尺度因子

尺度参数和限定了Gabor滤波器的空域作用范围。滤波器的尺度与频率成反比，根据不同的频率构造一组多尺度自相似小波，实现不同尺度滤波器模拟不同频率纹理的目的。本文设置α=1/ω。高斯窗函数的长短轴比例β/α决定椭圆的形状。固定频率和角度参数，尺度因子与可分性指标的关系如图4所示。可知当尺度因子小于2.5时，可分性指标随着因子增大而明显增大;当尺度因子大于2.5时，系统性能随因子增加变化明显。据此，选择β/α=2.5，系统性能接近最优。

2.3 特征编码

将归一化之后的图像Inorm划分为Nrmax×Nθmax个子块，每个子块与滤波器Gk(i，j)的窗口大小一致。对每个子块内积运算，按式(4)和式(5)处理，将实部和虚部的系数分别转化为二值化编码hRe和hIm，将所有子块的二值化编码按一定顺序组成虹膜特征编码。

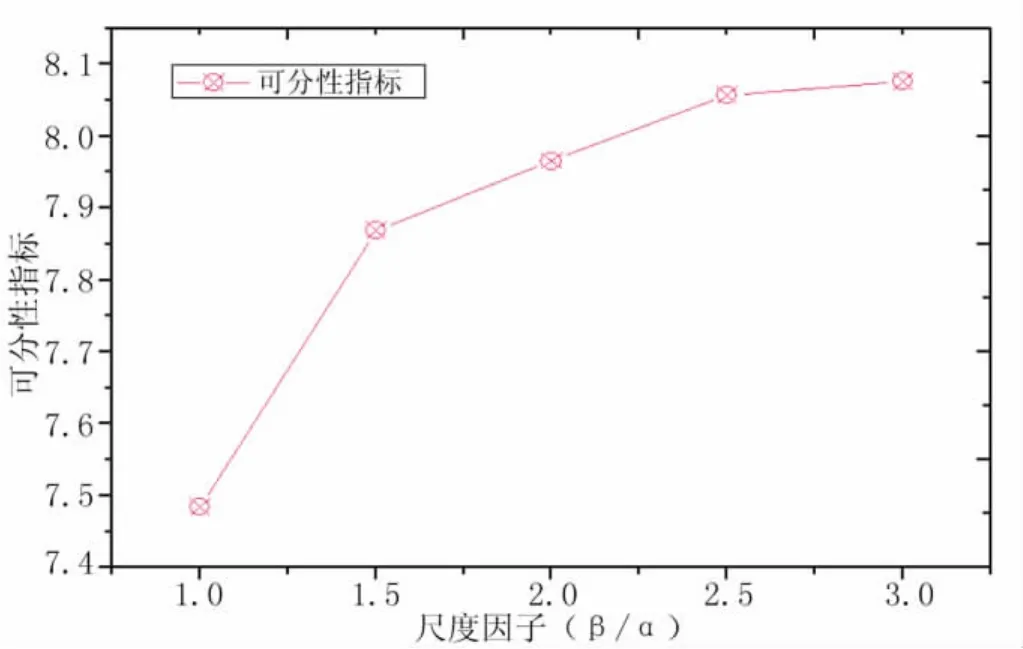
图4 尺度因子与可分性指标的关系曲线

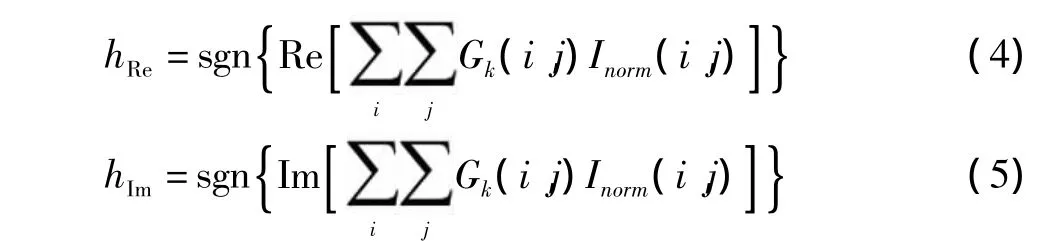
式中:Nrmax为按r方向划分得到子块的最大数目;Nθmax为按θ方向划分得到子块最大数目。

3 模板匹配

虹膜匹配通过特征向量的海明距离实现，即对两个长度相等的特征向量进行位异或处理，公式为

式中:Ai和Bi分别为特征向量A和B的第i位;T为特征向量的长度。

头部旋转、倾斜和眼睛回旋都会造成虹膜特征的移位。为了将虹膜特征点配准，匹配阶段引入适当的角度补偿。在没有角度补偿的情况下，归一化的虹膜角度区域为［π，2π］，注册时只保存一个特征模板;进行补偿之后，注册时对归一化之后的虹膜区域进行角度偏移处理，并保持若干注册模板。输入虹膜与注册模板中的最小海明距离作为匹配距离，公式为

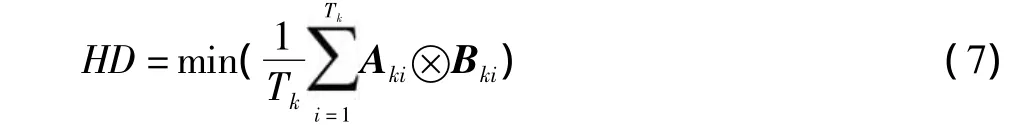
式中:k为角度补偿系数。由此可知算出系统的对角度偏移自适应范围θc，公式为

式中:N为归一化后角度方向的矩形图像宽度。

4 实验及结果

实验采用自建虹膜图像数据THP－Iris V1.0进行测试。从数据库中随机选取300人的左右眼4134 幅虹膜图像作为训练样本，随后从其余的图像中随机选取150人的左右眼2358 幅虹膜图像作为测试样本，将测试样本分为3组，每组由50人的左右眼的虹膜图像组成。

4.1 可分性指标与频率关系实验及分析

固定滤波器的方向角为 π/6，2π/6，3π/6，4π/6，5π/6，尺度因子为2.5。滤波器的频率直接通过海明距离的统计方差和均值影响识别性能，如图5所示。类内海明距离统计方差在频率为1/14时有明显的突变，表明滤波器的频率太大，容易引入高频干扰。故滤波器频率的选择不能太大也不能太小。在频率为1/20附近，类内海明距离统计方差分布稳定且较小，类间海明距离统计方差也比较小且变化相对缓慢。

图5 海明距离统计概率分布均值及方差与频率变化的曲线

4.2 可分性指标与角度关系实验及分析

固定滤波器组的频率为 16，18，20，22，24;尺度因子为2.5。海明距离概率分布统计均值和方差与角度变化的曲线如图6所示。可知，方向角度对海明距离统计均值影响不是很明显，而主要影响概率分布统计方差的变化。角度较小或较大时，方差值较大，表明滤波器提取的特征较少，减小了同类样本之间的相似性和不同类样本的差异性。

4.3 虹膜识别系统性能测试实验

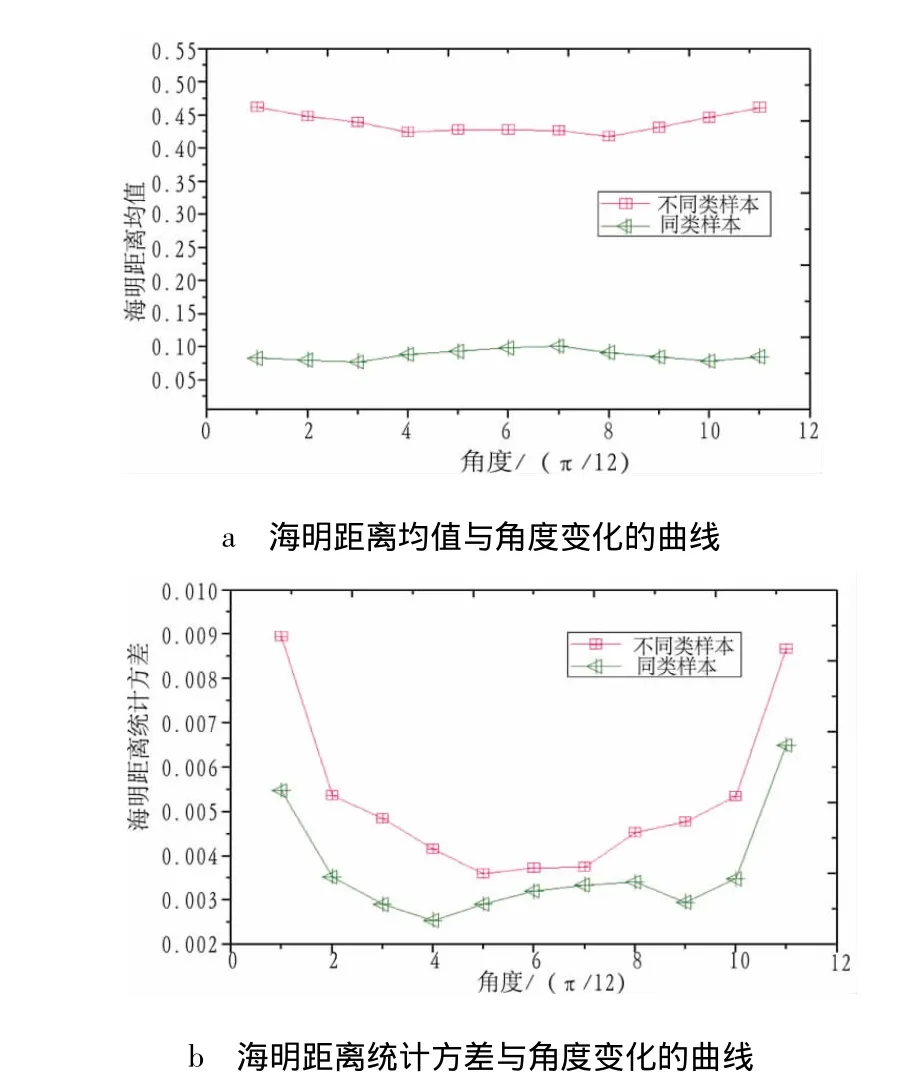
图6 海明距离统计概率分布均值及方差与角度变化的曲线

图7 海明距离分布ROC曲线(截图)

为了达到的测试目的，从自建虹膜图像数据库THPIrisV1.0中各选择100人的左右眼约1000 幅虹膜图像构成训练和测试样本集，记为Data1和Data2。通过训练样本获取的参数包括滤波器组的频率、角度方向、滤波器尺度因子比例和角度补偿系数。以这些关键参数构成虹膜识别算法系统，通过测试样本集获得系统的综合识别性能。根据样本训练的结果，得到系统一组关键参数。滤波器频率为16，18，20，22，24;角度频率为 π/6，2π/6，3π/6，4π/6，5π/6;尺度因子为2.5。算法在测试样本与训练样本上的运行性能指标见表1。

表1 算法在测试样本与训练样本上的运行性能指标

测试样本海明距离的概率分布和ROC曲线如图7所示。

5 结论

本文总结了二维Gabor滤波器组频率、方向和尺度因子参数与可分性指标之间的变化规律，设计出滤波器各参数的最优值。合适的角度补偿系数提高系统对头部倾斜、眼睛旋转等情况的自适应性。今后将结合局部二值模式对虹膜特征表达进行研究。

［1］DAUGMAN J G.High confidence visual recognition of persons by a test of statistical independence［J］.IEEE Trans.Pattern Analysis Machine Intelligence，1993，15(11):1148－1161.

［2］WILDES R P A.Iris recognition:an emerging biometric technology［J］.Proceedings of the IEEE，1997，85(9):1348－1363.

［3］BOLES W W，BOASHASH B.A human identification technique using images of the iris and wavelet transform［J］.IEEE Transaction on Signal Processing，1998，46(4):1185－1188.

［4］MA L，TAN T，WANG Y，et al.Efficient iris recognition by characterizing key local variations［J］.IEEE Transaction on Image Processing，2004，13(6):739－750.

［5］FITZGIBBON A，PILU M，FISHER R.Direct least square fitting of ellipse［J］.IEEE Trans. Pattern Anal. Mach. Intell.，1999，21(5):476－480.

［6］DAUGMAN J G.Uncertainty relation for resolution in space，spatial frequency，and orientation optimized by two－dimensional visual cortical filters［J］.Journal of the Optical of America A，1985，2(7):1160－1169.

［7］LEE T S.Image representation using 2D gabor wavelets［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1996，18(10):1－13.

［8］陈瑞，林喜荣.基于AdaBoost算法的快速虹膜检测与定位［J］.清华大学学报:自然科学版，2008，48(11):1923－1926.

［9］马进涛，陈瑞，林喜荣.基于弥散圆的虹膜图像采集自动调焦方法［J］. 电视技术，2009，33(S2):214－216.

［10］苑伟琦，冯琪，柯丽.基于单频率2D－Gabor滤波器的虹膜别算法的研究［J］. 光学技术，2010，36(1):20－24.

［11］陈丽娟，杨国军，陈瑾，等.先锋遗传算法在多峰值函数优化中的应用［J］. 电子科技，2006，196(1):40－43.

［12］黄慧芳，胡广书.虹膜识别算法的研究与实现［J］.红外与激光工程，2002，31(5):404－407.