认知无线电中基于频谱聚合的频谱分配算法
胡 庆,赵力力
(重庆邮电大学通信与信息工程学院,重庆 400065)
0 引言
随着各种新兴无线通信技术的广泛应用,无线频谱资源逐渐成为当今社会最为紧缺的资源之一。另一方面,各种无线通信系统的授权频谱的利用率非常低,在很多时候授权频谱并没有被充分利用。认知无线电[1-2]被认为是解决频谱资源稀缺的有效方法,它让认知用户(Cognitive User,CU)感知主用户(Primary User,PU)没有使用的频谱,并在不对主用户造成干扰的前提下使用这些频谱。
频谱分配作为认知无线电中非常关键的技术之一,目前对其已经有了很多研究。文献[3]中提出了一种颜色敏感图论着色(CSGC)算法,该算法考虑到了各认知用户可用频谱的差异性和频谱效益的差异性,并分析了在协作式和非协作式条件下频谱分配的差异。文献[4]提出了一种分布式局部议价的分配算法,在新的频谱分配过程中考虑先前的频谱分配信息,根据上一次分配的结果,能够通过有限次数的计算适应拓扑的改变,作出有效的频谱分配策略。文献[3]和[4]都是分配多个频段给认知用户,在这种情况下,认知用户为同时接入多个分配到的频段,需采用频谱聚合技术,但是由于发射机的硬件约束,认知用户可以聚合的频谱范围是有限制的[5],并不是任何频谱都可以被聚合。如图1所示,认知用户感知到了A,B,C,D,E这5个不连续的可用频段,设备能够聚合的最大频谱范围(Max Spectrum Span,MSS)如虚线框所示,那么聚合频谱最高频率和最低频率之差必须小于MSS。

图1 不连续频谱
文献[6]提出了一种聚合意识的频谱分配算法,该算法把认知设备能够聚合的有限的频谱范围考虑进来,使得网络能够支持的认知用户数达到理想值。但是该算法采用的是集中式的分配方式,算法假设每个认知用户的可用频谱是相同的,这与实际的认知网络并不相符。本文利用图论着色模型,提出了一种基于频谱聚合的分布式频谱分配算法。算法考虑了认知用户的带宽需求和认知设备有限的频谱聚合范围。
1 系统模型
假设网络中有N个认知用户,总的可用频谱数为M,起始频率为F1L,终止频率为FMH,频段m的频率范围为[FmL,FmH],如图2所示。不同认知用户的带宽需求不同,其中用户n的带宽需求表示为Dn(n=1,2,…,N)。每个认知用户n可利用现有的任一频谱检测机制来检测自己的可用频谱,假设“空闲频谱感知→频谱分配→数据传输”为一个时间周期,在同一周期的频谱分配期间,认知用户的位置和可用频谱都是不变的。本周期分配结束后认知用户再进行下一周期的感知,然后再进行分配。

图2 总可用频谱
本文的分配模型采用图论着色模型,图论着色模型可由空闲矩阵、效益矩阵、干扰矩阵和分配矩阵描述。
效益矩阵R={rn,m}N×M表示用户n使用频段m所获得的效益,如带宽、吞吐量。若 hn,m=0,则 rn,m=0。本文的效益rn,m指频段m的物理带宽,单位为MHz。
干扰矩阵 C={cn,k,m|cn,k,m∈{0,1}}N×N×M表示两个竞争用户之间的干扰约束,cn,k,m=1表示用户n和用户k同时使用频段 m 会产生干扰。当 n=k 时,cn,k,m=1-hn,m。文中,干扰约束采用以发射机为中心的约束,此干扰约束可表示为若 Dist(tn,tk)≤ds(tn,m)+ds(tk,m),则 cn,k,m=1,其中Dist(tn,tk)表示发射机n和k之间的距离,ds(tn,m)和ds(tk,m)分别表示发射机n和k在频段m上的覆盖半径。
分配矩阵 A={an,m|an,m∈{0,1}}N×M,an,m=1 表示频段 m 分配给用户 n。A 满足:若 cn,k,m=1,∀n,k < N,m< M,则 an,m·ak,m=0。
把网络拓扑抽象成一个干扰图G(V,E,H),把每个频段映射为一个颜色,则频谱分配问题可转化成图G(V,E,H)的顶点着色问题。V是图G的顶点集,表示共享频谱的认知用户;H表示顶点的颜色列表,即可用频谱集合;E是边集,由干扰约束集合C决定,当且仅当cn,k,m=1时,两个不同的顶点之间有一条颜色为m的边。图3为干扰图的一个例子,图中Ⅰ,Ⅱ,Ⅲ,Ⅳ,Ⅴ表示5个认知用户,它们之间的边即是由C决定的干扰约束,括号内的数字代表每个认知用户感知到的可用频谱。
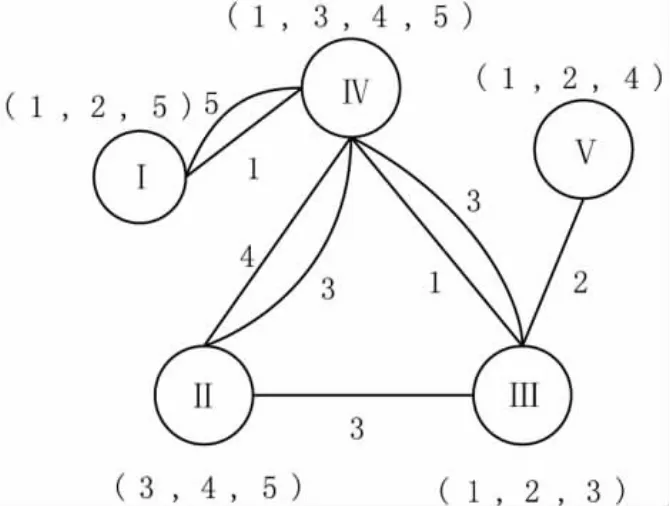
图3 干扰图的一个例子
2 优化问题
定义Chx为分配给某个认知用户的信道x,Chx=,m∈[1,M],其中和是分配给该用户的第i个频段的起始频率和终止频率,Nx为分配的频段数。
算法的分配目标是最大化认知无线电网络能够支持的用户数。令T表示网络支持的认知用户数,那么优化问题可表示为

约束条件为
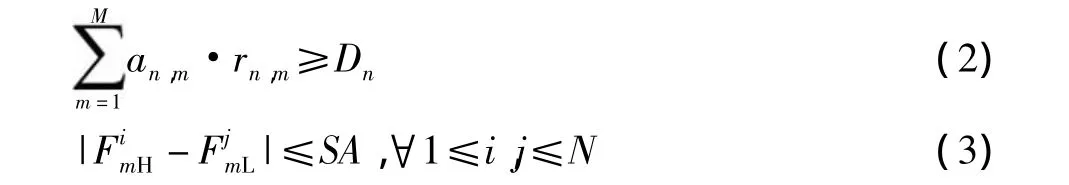
其中式(2)保证分配给认知用户n的带宽和能满足用户的带宽需求,式(3)保证分配给用户n的频段都是可以聚合的,这样分配后的频段认知用户才可成功接入。
现如今临床中运用TAXUSTM支架,作为EXPRESS支架表面,以多聚物涂层的慢速释放出紫杉醇,在现如今的临床应用中具备较好安全有效性。经临床研究发现PES植入半年后,运动诱因出现支架远端冠状动脉血管发生收缩,BMS引发血管舒张情况。
3 算法步骤
详细地算法步骤为:
1)根据标注规则计算图G中的每个顶点的标注值lable(n)及对应的颜色color(n),找到标注值最大的顶点n*=arg max label(n)。
2)计算顶点n*的可用频谱的带宽和是否满足带宽需求,若不满足就从图G中删除该顶点;若满足则进入步骤3)。
3)依次从低频到高频判断在MSS内是否有可用频谱的带宽和满足带宽需求,设v表示顶点n*的可用频谱数,即从第1个到第v个可用频谱的起始频率开始判断在MA内是否有可用频谱的带宽和满足带宽需求。若有,则按color(n)值从大到小分配直到该顶点的带宽需求得到满足;若没有,则从图G中删除该顶点。
4)返回第一步,循环此过程直到图G为空。
在分配过程中,当顶点n*每次分配后都要从与其有干扰的顶点的可用频谱中删除已分配的频谱。标注规则如
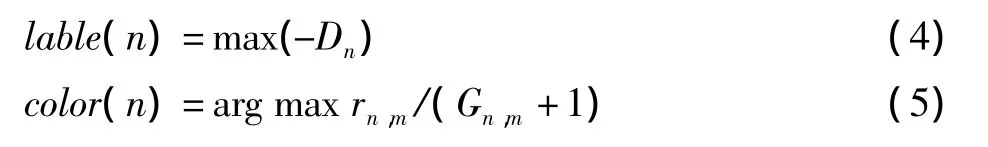
本算法确定顶点后依次从该顶点的第1个到第v个可用频谱的起始频率开始判断在MSS内是否有可用频谱的带宽和满足带宽需求,分配的频段必定是在最大聚合范围MSS之内的,即可聚合的。
4 仿真分析
在(200×200)区域内随机部署N个认知用户,仿真频率为500~700 MHz,其中包括了部分模拟广播电视频段。网络拓扑随机生成,用户带宽需求Dn在7~14 MHz之间随机取整数值,MSS=40。H矩阵为随机生成的0-1矩阵,干扰约束由 Dist(tn,tk)≤ds(tn,m)+ds(tk,m)生成,覆盖半径ds在[1,4]内随机生成。R 矩阵在[7,14]随机生成。本文将本算法与文献[3]中的CSGC算法进行比较,CSGC算法中有3种合作式的标注规则:CSUM,CMIN和CFAIR。
图4为当网络中总的可用频谱数变化时两种算法的认知用户接入率,N=20。从图中可以看出,SADSA算法明显优于CSGC算法,当总的可用频谱数逐渐增大时,优越性更加突出,这是因为当总可用频谱数增加时,没有考虑频谱聚合的CSGC算法使得认知用户分配到的频谱不能聚合的概率在随之增大,即认知用户不能接入分配到的频段的概率在增大。
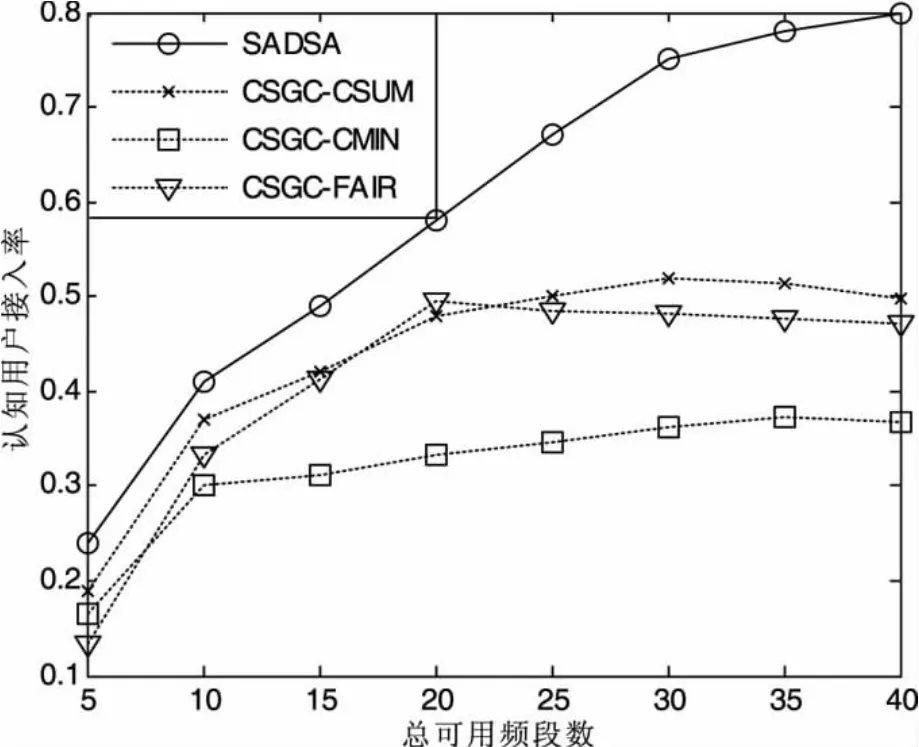
图4 总可用频段数不同时的接入率比较
图5是当认知用户数变化时,SADSA算法与CSGC算法的比较。当认知用户数增加时,可用频谱数不变,M=15。从图中可以看出,这种情况下本文的算法依然优于CSGC算法,其原因是CSGC算法并没有考虑认知设备可聚合的频谱范围的有限性。

图5 不同认知用户数下的接入率
5 小结
认知无线电网络的一个重要特点就是认知用户感知到的可用频谱的不连续性,为满足认知用户较高的带宽需求,需利用频谱聚合技术将多个频段聚合在一起使用。但是由于硬件条件的限制,可以聚合的频谱范围是有限制的,所以频谱分配算法应当考虑到这种限制,以使认知用户能够接入自己分配到的频谱。本文提出了一种认知无线电网络中的频谱分配算法,算法以广泛应用于各种无线网络中资源分配的图论着色为分配模型。算法考虑到了可用频谱的不连续性和频谱聚合的有限性,仿真结果证明了本文算法的优越性。
[1]JOSEPH M,GERALD Q,MAGUIRE J R.Cognitive radio:making software radios more personal[J].IEEE Personal Communications,1999,6(4):3-18.
[2]畅志贤,石明卫.认知无线电技术综述[J].电视技术,2007,32(31):130-133.
[3]PENG C,ZHENG Haitao,ZHAO B Y.Utilization and fairness in spectrum assignment for opportunistic spectrum access[J].Mobile Networks and Applications,2006,11(4):555-576.
[4]CAO Lili,ZHENG Haitao.Distributed spectrum allocation via local bargaining[C]//Proc.IEEE SECON '2005. [S.l.]:IEEE Press,2005:475-486.
[5]JIA Juncheng,ZHANG Qian.Hardware-constrained multi-channel cognitive MAC[C]//Proc.Global Telecommunications Conference.[S.l.]:IEEE Press,2007:4653-4658.
[6]CHEN D,ZHANG Q,JIA W.Aggregation aware spectrum assignment in cognitive ad-hoc networks[EB/OL].[2011-04-06].http://ihome.ust.hk/~dwchen/download/AASA_crowncom2008.pdf.

