基于特征融合的水下目标识别方法

张铭钧，张丽，万媛媛

(1.哈尔滨工程大学 水下智能机器人技术国防科技重点实验室，黑龙江 哈尔滨 150001;2.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

水下目标识别是水下机器人智能化领域研究的重要内容之一［1］，由于水体对光线的散、折射作用和吸收效应以及水流、光照条件的影响，使得采集到的水下图像存在较强的模糊性、失真且信息冗余.又由于水下成像环境的特殊性，使得利用图像的单一特征难以完全表述目标物的特征属性，而图像的多类特征的提取可能造成信息之间的冗余性，因此，合理取舍或融合水下图像的各类信息是保证水下目标物识别准确率的一个关键因素［2］.针对水下灰度图像模糊的特点，文献［3］将迭代的双边滤波算法应用于Canny边缘检测，基于直线连接度量的Hough变换，获取全局和局部坐标系下定义的图像曲线，完成参数单元主动搜索空间特征点的模板匹配Hough变换，但Hough变换自身存在计算量大、耗费存储空间大的不足.文献［4-5］构造出离散状况下同时具有旋转、缩放和平移不变性的Hu氏不变矩描述目标物形状特征，一定程度上提高了目标识别准确率，但该方法忽略了摄像机镜头畸变对特征提取准确性的影响.为提高目标识别准确率，文献［6］利用广义典型相关分析对Gabor特征进行特征融合，采用监督近邻保留嵌套算法对高维彩色图像特征进行降维，该方法可以显著提高识别系统性能，但是水下彩色图像通常会出现较严重的色彩丢失和失真现象，使得该算法在水下图像处理领域应用受到限制.

为更全面表述水下目标物本质属性，提高目标识别准确率，本文在文献［4-5］提取目标形状特征的基础上增加径向畸变的影响因子，改进了Hu氏不变矩;同时基于相似度量准则对形状特征向量进行降维处理;最后给出一种基于线性加权求和进行特征融合的方法，文中融合了目标的特征和纹理特征，弥补了文献［4-5］中仅利用形状特征来表征目标物时信息的不全面.通过水下目标特征提取和识别实验验证了本文方法的有效性.

1 改进Hu氏不变矩提取形状特征

Hu氏不变矩是提取灰度图像形状特征的常用方法之一.然而在实验研究中发现，由于传统的Hu氏不变矩忽视成像过程中镜头畸变的影响，所以存在图像几何矩偏离目标真实特征的问题.针对此问题，本文提出了一种改进的Hu氏不变矩提取形状特征方法，通过反解径向畸变模型恢复图像的理想像素坐标，建立图像像素坐标与灰度值的映射关系，在此基础上重新构建了新的具有平移、缩放和旋转不变性的Hu氏不变矩.

在建立形状特征向量前，传统Hu氏不变矩首先定义了图像的p+q阶几何矩［4］:

式中:M×N为图像大小，f(x，y)为图像像素的灰度值，x和y分别为像素点的横纵坐标，mpq为图像区域几何矩.

定义图像p+q阶几何矩后，文献［4］又推导出了在离散情况下同时具有平移、缩放和旋转不变性的6个矩特征向量.

式(1)中几何矩的准确性建立在图像无畸变的基础之上.在实际成像过程中，摄像机光学系统并不是精确地按理想针孔成像原理工作，物体点在成像面上的实际成像与理想成像之间存在光学畸变误差，使得图像像素坐标(x，y)及其灰度值f(x，y)不能一一对应，造成式(1)中几何矩偏离目标真实特征.为消除径向畸变误差，本文通过反解摄像头径向畸变模型恢复像素坐标与其灰度值的映射关系，修正图像p+q阶几何矩.

一般将径向畸变模型定义［7］为

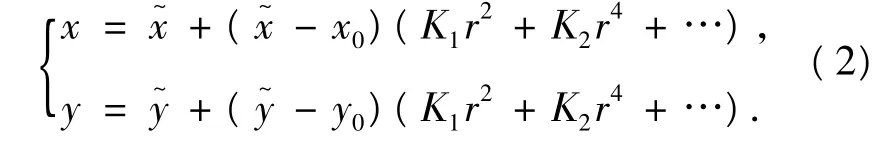
式中:(x，y)为受畸变影响的真实像素坐标，(x～，y～)为理想图像像素坐标，(x0，y0)为图像中心像素坐标.Ki为2i阶径向畸变系数，畸变程度与目标点到图像平面中心的距离r有关，有

研究中发现，仅考虑二阶径向畸变系数就足以描述摄像头径向变形情况，因此可忽略畸变模型中的高阶畸变项，简化径向畸变模型.对简化后的模型反解得到目标点的理想像素坐标2

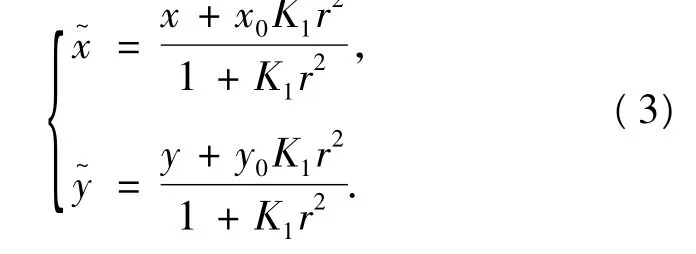
将理想像素坐标带入式(1)获得修正后的图像p+q阶几何矩:

结合式(3)和文献［4］即可获得新的具有平移、缩放和旋转不变性的Hu氏不变矩.改进后的Hu氏不变矩在构造几何矩时增加了径向畸变影响因子，减小了镜头变形对识别准确性的影响.

2 形状与纹理特征融合

为避免Hu氏不变矩识别精度不高及单一形状特征难以精确表述目标物属性问题，本文提出一种将形状特征和纹理特征相融合的方法，根据相关特征向量间线性组合不影响其不变性的特点，融合相似形状特征，由贡献率的大小选取最佳纹理特征;由于三阶矩和形状特征向量均表达图像的统计特征，利用线性加权求和的思想将三阶矩设定权重后直接融入形状特征向量，最终建立融合特征向量来描述水下目标信息.

2.1 形状特征向量选取

为降低形状特征向量信息间的冗余性，针对传统降维处理方法直接通过去除形状特征高次项引起形状描述不精准的问题，提出一种基于相似度量准则进行特征降维的方法.该方法利用空间夹角余弦定理度量向量相似性，有效避免了相关系数法在度量特征向量相似性时存在的正、负相关合并的问题，根据相关向量间线性组合并不改变向量自身性质的特点，将相似向量线性相加求平均，构造出新的形状特征向量.

Hu氏不变矩提取得到的形状特征向量之间并不完全独立，存在信息的冗余.本文在研究中发现，特征向量间的冗余性与它们的相似度有着密切关系，向量相似度越大，说明2个特征向量间线性密切程度越高，因此，可以通过求取特征向量间的相似度来判断信息的冗余与否，然后利用权重分配的方式对相似度等于或趋近于1的特征向量进行融合，降低特征向量的维数.

文献［8］给出一种特征向量相似性的度量方法，该方法基于相关系数法将向量间的相似度分为3种情况:正相关、不相关和负相关.这种分类方法在表达特征向量间的相似度时，为保证相似度取值范围为［0，1］，还需要将正、负相关合并到一起，增加了算法的复杂性.

本文在对形状特征向量的求取中发现，特征向量各特征值均为正值，因此各向量之间的夹角范围在［0，π/2］内，求取夹角的正、余弦值即能保证相似度的取值范围在［0，1］内，两特征向量Mi与Mj之间的相似度可以表示为

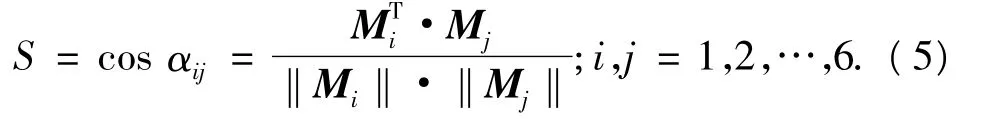
式中:αij表示向量Mi与向量Mj间的夹角，S值越大说明向量相似度越高.

利用式(5)计算得到特征向量间的相似度，若两向量间相似度趋近于1，则认为两向量为相关特征向量，根据相关特征向量的线性组合并不改变向量自身性质的特点，可以通过线性组合求平均对形状特征向量进行融合，降低其维数.

为说明形状特征向量融合的具体步骤，本文在1.2 m ×1.2 m ×0.8 m 的水箱环境下，采用 EL-241C高解析度水下摄像头及OK-M10A图像采集卡实时获取4种具有不同形状或纹理的典型目标物进行分析，目标物如图1所示，其中纹理椭球体与椭球体具有相同的形状.

为说明本文方法的有效性及普适性，实验针对上述4种目标物从多个方位、不同光照条件下各采集100幅图像.利用式(4)提取形状特征，得到6个形状特征向量均值如表1所示，表中Mi(i=1，2，…，6)表示第i个特征值.

图1 水下目标物图像Fig.1 The images of underwater targets

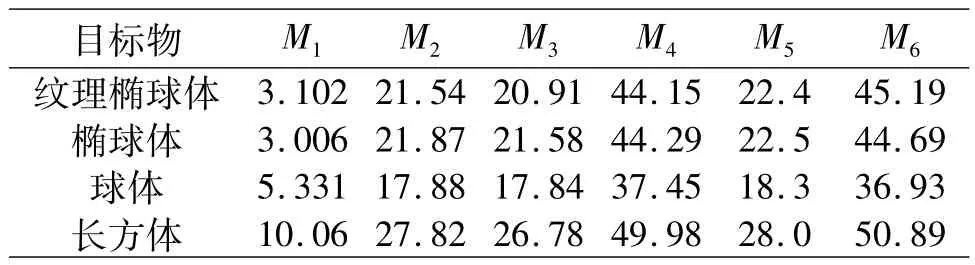
表1 4种目标物特征向量均值比较Table 1 The comparison of feature vectors mean about four types of targets

通过对表1数据和式(5)的计算可知，M2、M3，M3、M5及 M2、M5之间的相似度分别为 99.990 7%、99.990 3%、99.991 6%，M4与 M6之间的相似度为99.991 7%，因此本文认为 M2、M3、M5之间及 M4、M6之间特征向量具有相似性(也称相关性).根据相关特征向量线性组合并不改变向量自身性质的特点，可以将 M2、M3、M5和 M4、M6进行线性组合消除特征向量间的冗余问题.进一步分析表1，以最大误差表征各特征向量间的差异度，M2、M3和M5之间的最大误差仅为4.1%，M4与M6之间的最大相对误差仅为2.3%，因此特征向量间不仅具有高相似性，并且在数值上比较接近.基于这种分析，可以直接将相似特征向量进行线性相加求平均.新构造降维后的形状特征向量为

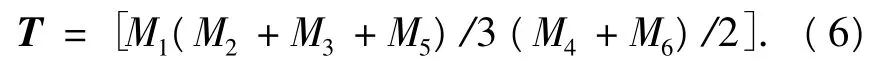
采用新构建的3个特征值作为分类器的输入向量，避免了相关特征向量信息间的冗余，降低维数简化了分类器的设计，降维后的特征值如表2所示.

表2 降维后的目标物形状特征向量值Table 2 The shape feature vectors of the targets dimension-reduced

2.2 最佳纹理特征选取

由于水下噪声污染严重使图像轮廓信息丢失严重，仅利用2.1节得到的形状特征向量难以准确分类水下目标物.鉴于图像纹理在表达目标物表面属性上的优越性，结合统计法［9］和 Fourier频谱法［10］，构造图像的纹理特征向量，弥补仅依靠单一形状特征造成的目标识别率低的问题.本节通过对纹理特征的分析，旨在提取适应于复杂水下环境中的最佳纹理特征向量.

针对灰度图像的纹理特征描述，文献［9］列出了其空间域内的统计度量:标准差、平滑度、三阶矩、一致性和熵.其中，标准差和平滑度描述了图像灰度对比度，受噪声影响严重;一致性和熵作为像素分布的概率统计，易受光照条件的影响;而三阶矩是对图像灰度分布偏离对称情况的度量，在求取中通过各灰度与图像均值作差，一定程度上平滑了随机噪声的干扰，因此，在描述图像的纹理特征上三阶矩较其他纹理统计量有更强的抗噪能力.

针对三阶矩难以检测图像全局纹理模式的问题，本文结合频谱图惯性矩和分布方差表达图像纹理的粗细程度和纹理走势，弥补统计度量在表征纹理细节上的不足.

为了进一步说明3种纹理特征向量选取的合理性，本文对采集得到的每种水下目标物的100幅图像提取图像的纹理特征，其度量准则包括:标准差σ、平滑度R、三阶矩μ3、一致性U、熵E、频谱图惯性矩S(r)及分布方差S(θ)，得到的纹理特征平均值如表3所示.

分析表3中数据，对于纹理椭球体和椭球体，标准差、平滑度、三阶矩、一致性、熵、惯性矩及分布方差的相对误差分别为 5.9%、18.5%、53.2%、3.35%、1.3%、22.8% 和 89.2%.可见对于识别本文中纹理椭球体和椭球体的纹理特征，三阶矩、惯性矩及分布方差的贡献最大，平滑度次之，标准差、一致性和熵的贡献最小.由于所选取的目标物纹理具有随机性，能够代表水下纹理目标的一般情况，因此从理论分析和实验数据中均可以证明，选取三阶矩、惯性矩和分布方差作为纹理图像的特征向量的方法是可行的.

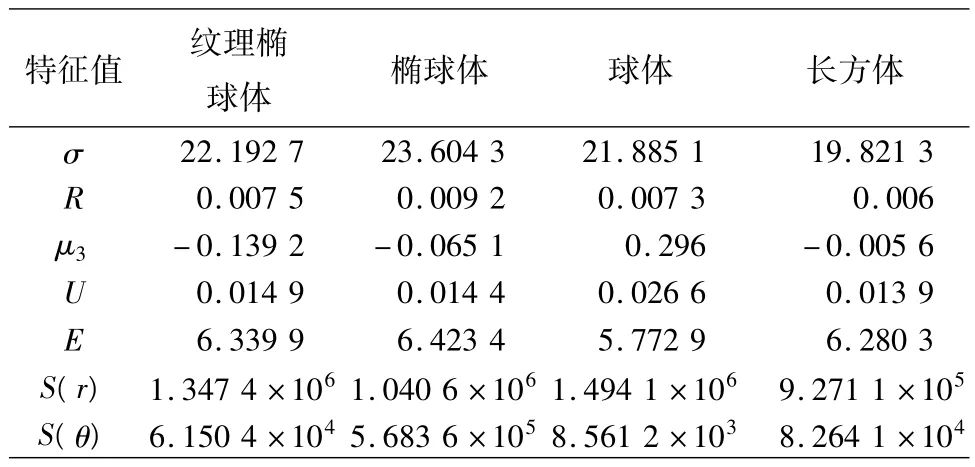
表3 统计法及频谱图得到的纹理特征平均值Table 3 The texture feature mean value through statistic method and spectrum

2.3 特征融合

2.1和2 .2节分别介绍了基于相似度量准则降低形状特征向量维数的方法及最佳纹理特征的选取过程.若直接组合3个形状特征及3个纹理特征，则容易因各特征向量权重而造成目标误判，针对此问题提出一种基于线性加权求和融合特征向量的方法.

本文在研究中发现，三阶矩主要描述图像的灰度分布特性，形状特征向量同样是基于图像的统计原理构造的几何矩，本质上具有相通性，因此可以直接利用线性加权求和的方式构造新的融合特征向量.由表2和3中数据，形状特征向量约为三阶矩的8～104倍，将三阶矩加权重后直接与形状特征向量分别相加，得到融合后的特征向量如式(8)所示，特征值如表4所示:

式中:Fi表示了第i个融合特征向量，Wμ、Wt分别为各特征的权重，并且Wμ+Wt=1.

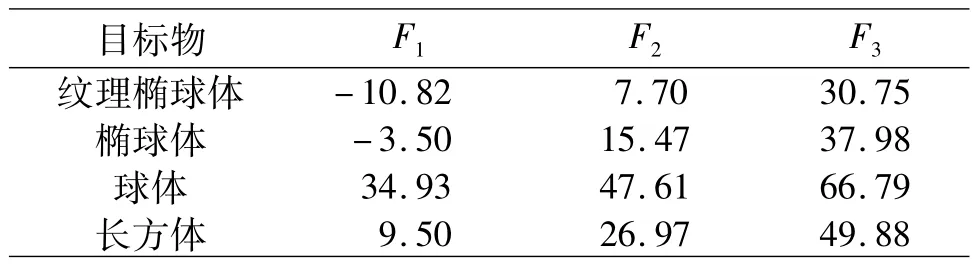
表4 融合特征值统计Table 4 Fused eigenvalue statistics

表2中纹理椭球体与椭球体的形状特征值近似，最大相对误差仅为3.1%，但表3中两者的三阶矩特征值相对误差达到53.2%.通过本文提出的量化特征进行数据融合，得到表4中融合后的3个特征值，其相对误差分别为 67.6%、50.2%、19.0%，能够作为识别相同形状目标物的特征向量.

三阶矩仅描述了图像灰度分布信息，为了表征整幅图像纹理的变化规律，提高特征向量中纹理特征的贡献率，在上述3个特征向量的基础上，加入表4中表征纹理粗细和走向的特征向量，最终获得的融合特征向量:

融合特征向量表述了水下目标的形状特征、图像灰度分布规律、纹理粗细及走向特征，较Hu氏不变矩能够更全面地表征目标信息.

3 水下目标特征提取和识别实验

3.1 改进Hu氏不变矩水下目标识别实验

实验选取图1所示的目标物，对每种目标物从多个方位、不同光照条件下各采集70幅图像作为样本.首先采用传统的Hu氏不变矩提取其形状特征，以每种目标物的均方差来表示其形状特征向量的稳定性，结果如表5所示.

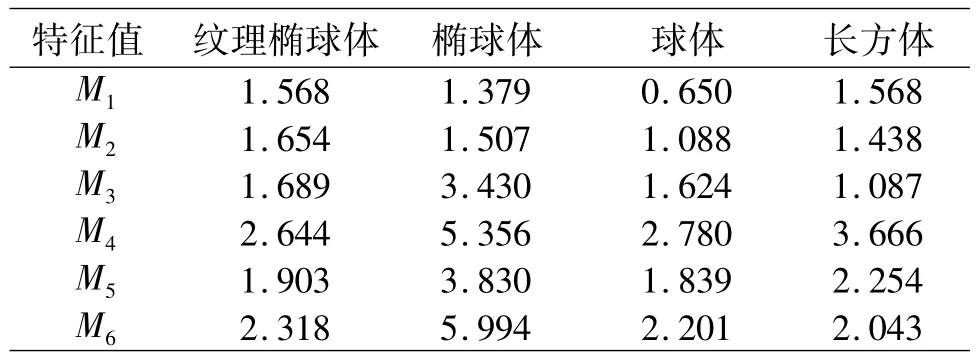
表5 传统Hu氏不变矩的特征值均方差Table 5 Eigenvalue mean-square deviation obtained by traditional Hu moment invariants

由表5中数据可知，采用传统Hu氏不变矩提取的目标物特征值均方差普遍偏大，介于0.650和5.994之间，其中椭球体的形状特征提取时的波动最大.将采用传统Hu氏不变矩得到的形状特征向量作为BP神经网络的样本输入，目标物识别结果如表6所示.

表6 传统Hu氏不变矩目标识别结果Table 6 The target recognition results of traditional Hu moments invariants

由表6可以看出，利用传统Hu氏不变矩提取的形状特征来识别目标物，最终得到的识别准确率普遍很低，尤其纹理椭球体识别准确率不足50%，长方体形状异于其他三类，识别率最高也仅为80%.

采用本文提出和改进的Hu氏不变矩提取形状特征，特征值均方差如表7所示，括号内数值表示与传统Hu氏不变矩提取形状特征实验数据(见表5)相比，均方差的相对减小量.从表7中数据可以看出，采用所提出的改进Hu氏不变矩提取得到的目标物形状特征向量的稳定性得到改善，其中，纹理椭球体和椭球体的稳定性提高幅度最大，均方差的最大相对减小量分别达到62%和83.3%;球体次之，最大相对减小量为52.9%;长方体最弱，最大相对减小量为46.5%.

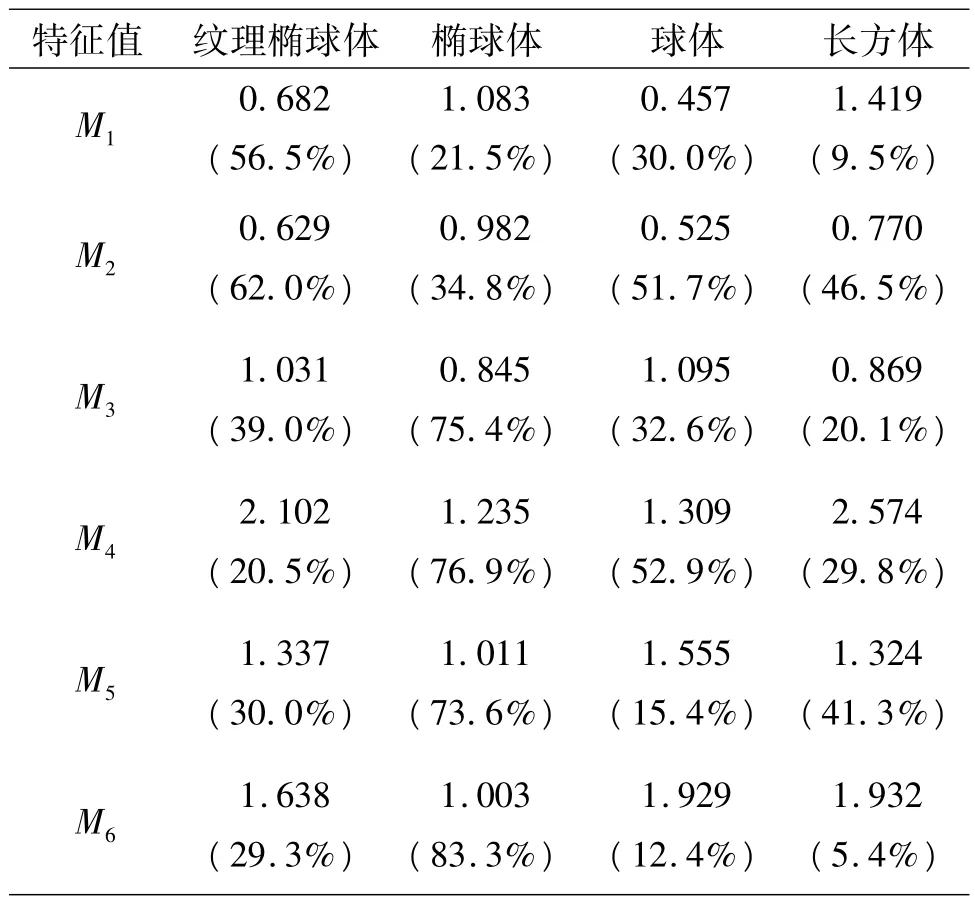
表7 改进Hu氏不变矩特征值均方差Table 7 Eigenvalue mean-square deviation obtained by modified Hu moment invariants

将改进Hu氏不变矩提取的目标物形状特征向量作为BP神经网络的样本输入，得到的目标识别结果如表8所示.括号中数据为相对于传统Hu氏不变矩目标识别率(见表6)的提高量.

表8 改进Hu氏不变矩目标识别结果Table 8 The target recognition results of modified Hu moments invariants

对比表6和8中数据，采用改进Hu氏不变矩后，纹理椭球体、椭球体、球体和长方体的识别准确率分别提高了 4.3%、5.8%、10.0% 和 7.1%，其中球体的识别率提高程度最大.主要原因在于改进的Hu氏不变矩校正了摄像头径向畸变产生的目标形状失真.

通过对比实验进行结果分析:1)与传统的Hu氏不变矩相比，本文提出的改进Hu氏不变矩考虑了摄像头径向畸变的影响，使目标物的识别准确率和稳定性都得到了一定程度的提高;2)传统的和改进的Hu氏不变矩都只能提取目标物的形状特征，难以识别具有相同形状、不同纹理的纹理椭球体和椭球体，因此改进Hu氏不变矩前后，纹理椭球体和椭球体的识别率都很低;3)由于影响水下目标物特征提取的因素很多，造成图像失真的原因不唯一，而本实验仅考虑摄像机径向畸变的影响，因此本文提出的改进Hu氏不变矩只能在一定程度上提高目标物样本的识别准确率.为更加全面地提取目标物属性特征，进一步提高目标识别的准确率，本文将目标物形状和纹理特征进行融合及如下实验验证.

3.2 融合特征向量水下目标识别实验

实验仍采用纹理椭球体、椭球体、球体和长方体作为目标物，针对采集得到的70幅图像样本进行融合特征向量的计算，将该融合特征向量作为BP神经网络的样本输入，最终输出的目标识别结果如表9所示.括号内数据表示相对于表8中识别率的提高量.

表9 融合特征向量目标识别结果Table 9 The target recognition results of fused eigenvectors

由表9数据可知，采用融合特征向量识别目标物使纹理椭球体、椭球体、球体和长方体的识别率分别提高了 31.8%、24.1%、45.5%、7.8%，4 种目标物的识别率均超过了84.3%.对纹理椭球体的识别率提高幅度最大，椭球体次之，球体再次之，对长方体的识别率提高幅度最小.

通过表8和9的数据进行对比分析:1)纹理特征的加入不仅提高了相同形状、不同纹理目标物的识别率，也提高了形状、纹理均不同的目标物的识别率;2)融合特征向量的引入提高了水下目标识别率，证明本文提出的形状与纹理特征相融合的目标识别方法的有效性，也间接证明了形状特征向量降维处理的合理性.

4 结束语

本文探讨了水下目标物的特征提取方法，提出了一种基于特征融合的水下目标识别方法.通过增加径向畸变的影响因子，重新构造了新的不变矩;依据相似度量准则对形状特征向量进行降维处理，解决了其中的冗余问题;最后应用线性加权求和的方法融合形状特征和纹理特征.通过实验表明，基于融合特征的水下目标识别方法解决了镜头畸变对图像失真的影响、目标形状描述冗余问题，并且通过融合形状特征和纹理特征，丰富了目标本质属性的描述，提高了不同目标物的识别准确率.

［1］徐玉如，肖坤.智能海洋机器人技术进展［J］.自动化学报，2007，33(5):518-521.XU Yuru，XIAO Kun.Technology development of autonomous ocean vehicle［J］.Acta Automatica Sinca，2007，33(5):518-521.

［2］SUN Q，ZENG S，LIU Y.A new method of feature fusion and its application in image recognition［J］.Pattern Recognition，2005，38(12):2437-2448.

［3］NEGRE A，PRADALIER C.Robust vision-based underwater target identification and homing using self-similar landmarks［J］.Field and Service Robotics，2008，42:51-60.

［4］唐旭东，朱炜，庞永杰，等.水下机器人光视觉目标识别系统［J］.机器人，2009，31(2):171-178.TANG Xudong，ZHU Wei，PANG Yongjie，et al.Target recognition system based on optical vision for AUV［J］.Robert，2009，31(2):171-178.

［5］CHEN Y，ZHANG M，Local moment invariant analysis［C］//Proceedings of the Conference on Computer Graphics，Imaging and Vision:New Trends 2005.Piscataway:Institute of Electrical and Electronics Engineers Computer Society，2005:137-140.

［6］黄晓华，王春茂，郑文明.基于彩色人脸图像的信息融合与识别方法［J］.中国图象图形学报，2010，15(3):422-428.HUANG Xiaohua，WANG Chunmao，ZHENG Wenming.An information fusion and recognition method for color face images［J］.Journal of Image and Graphics，2010，15(3):422-428.

［7］王富治，黄大贵.基于图像差分的精密畸变校正研究［J］.仪器仪表学报，2010，31(2):377-382.WANG Fuzhi，HUANG Dagui.Accurate distortion correction study based on differential images［J］.Chinese Journal of Scientific Instrument，2010，31(2):377-382.

［8］张宇，刘雨动，计钊.向量相似度测量方法［J］.声学技术，2009，28(4):532-536.ZHANG Yu，LIU Yudong，JI Zhao.Vector similarity measurement method［J］.Technical Acoustics，2009，28(4):532-536.

［9］RASOUL K，MANSUR V，FARZAD T.Fully automatic segmentation of multiple sclerosis lesions in brain MR FLAIR images using adaptive mixtures method and Markov random field model［J］.Computers in Biology and Medicine，2008，38(3):379-390.

［10］SENGUR A.Wavelet transform and adaptive neuro-fuzzy inference system for color texture classification［J］.Expert System with Applications，2008，34:2120-2128.