一种对于分布式渲染集群系统可用性分析的概率模型检查方法

王克敏,王永滨

(中国传媒大学计算机学院北京 100024)

一种对于分布式渲染集群系统可用性分析的概率模型检查方法

王克敏,王永滨

(中国传媒大学计算机学院北京 100024)

本文通过使用概率模型检查工具PRISM,研究渲染集群节点系统的可用性。针对1个集群节点和2个集群节点组成的系统,使用PRISM模型语言进行了建模,并通过相关属性的描述,从而得到系统可用性的稳态概率分布。

概率模型检查;渲染集群;PRISM;CTMC;CSL

1 引言

分布式渲染集群系统可对外提供高性能的渲染服务,其系统服务的可靠性决定了其系统的服务质量。渲染集群中各节点在遇到故障时,其修复能力决定了整个渲染系统的可用性。而且当节点数目在进行扩展时,其可用性的保障对于整个系统的影响更为重要,如何有效地分析系统的可用性是一个值得研究和探讨的问题。

本文基于概率模型检查工具PRISM,对整个渲染集群系统进行了形式化建模,并通过其系统属性的描述,对系统的可用性进行了分析和验证。并通过假设其故障和修复速率,分析和预测了在不同情况下,系统可用性的概率分布。

本文的工作基于[1]的研究工作,在[1]文中,作者对系统可用性的概率分布进行了手工推演和计算。我们的工作旨在引进一种新的方式对其进行计算和验证,并通过直观形象的数据图表对其可用性进行进一步分析和探讨。针对1个集群节点和2个集群节点组成的系统,使用PRISM模型语言进行了建模,并通过相关属性的描述,从而得到系统可用性的稳态概率分布。

本文的内容如下组织:

第二部分,简要介绍一下分布式集群渲染系统;

第三部分,简要介绍一下概率模型检查工具PRSIM;

第四部分,重点介绍对于集群渲染系统可用性模型的PRISM形式化建模和分析;

第五部分,结论和下一步工作。

2 分布式集群渲染系统

在分布式集群渲染环境中,渲染集群和普通渲染Client共同承担渲染任务,集群节点一般采用HP等厂商生产的刀片服务器,因此集群节点的浮点计算能力要强于一般的渲染Client。这样在分解和分配渲染任务时,我们可充分考虑渲染集群和渲染Client的性能差异,让可靠性较高的集群节点承担较大比例的渲染任务。由此可见,在执行渲染任务过程中,集群的高可靠性、高可用性以及良好的可扩展性是系统向Web用户提供优质渲染服务的有力保障。如何对并行集群建立比较准确的模型,分析集群节点在平行扩展时所具有的高可用性是值得探讨和研究的重要问题之一,为构建面向Web用户的高可用渲染服务系统提供重要的量化依据。

针对集群系统的可用性分析,常用的建模方法包括可靠性框图、故障树模型、马尔科夫过程和随机Petri网等。

PRISM工具就是一个基于马尔科夫过程的概率模型检查。

3 概率模型检查工具PRSIM

PRISM是一个概率模型检查工具,适用于具有随机或概率行为的系统形式化建模与分析。PRISM工具支持三种概率模型:离散时间马尔可夫链(discrete-time Markov chains(DTMCs))、连续时间马尔可夫链(continuous-time Markov chains(CTMCs))和马尔可夫决策进程(Markov decision processes(MDPs)),以及由这些模型通过代价/回报引申出的模型。

PRISM工具已经被广泛应用于各种领域的系统分析,包括多媒体通信协议、随机化的分布算法、安全协议、生物系统等等。

在此工具中,系统模型通过PRISM语言进行描述,PRISM语言是一个非常简单的、基于状态的语言。PRISM工具支持对系统模型量化属性的自动分析,比如:“此系统24小时内由于错误停机的概率是多少？”、“在所有可能的初始条件下,一个协议由于错误中止的最坏概率是多少？”、“60分钟后一个消息队列的长度是多少？”、“此算法结束的最坏可能时间是多少？”。

该属性规范语言纳入了时序逻辑语言PCTL、CSL、LTL和PCTL*,以及定量规格扩展和代价/回报扩展。

PRISM纳入了先进的符号数据结构和算法,基于二叉决策图BDD(Binary Decision Diagrams)和多端二叉决策图MTBDDs(Multi-Terminal Binary Decision Diagrams)。

3.1 PRISM语言

PRISM语言可以声明三种类型的概率模型,离散时间马尔可夫链(discrete-time Markov chains(DTMCs))、连续时间马尔可夫链(continuous-time Markov chains(CTMCs))和马尔可夫决策进程(Markov decision processes(MDPs))。在模型定义的开始,可以使用关键字dtmc,ctmc或mdp加以声明,也可以分别写为probabilistic,stochastic和 nondeterministic。如果没有声明模型类型,默认类型是mdp。

具体关于其模块、变量、常量、表达式等的定义,请参看PRISM手册[2]。

3.2 PRISM属性规范

为了分析PRISM中构建的概率模型,需要描述出关于此模型的属性,当然,这些属性可以是一条,也可以是多条,它们通过PRISM工具对模型进行验证。PRISM的属性规范语言囊括了一些大家都比较熟悉的概率时序逻辑,包括 PCTL、CSL(Continuous Stochastic Logic)[3]、LTL 和 PCTL*。其中,PCTL用来描述DTMC和MDP类型的模型属性;CSL是用于描述 CTMC类型模型属性,它是PCTL的扩展;LTL和PCTL*可以用来描述DTMC和MDP类型模型属性,或是CTMC类型模型的非时间属性。

4 集群渲染系统可用性模型的PRISM形式化建模和分析

4.1 1个集群节点的可用性的PRISM建模与验证

[1]文中提出了一种关于1个集群节点的CTMC模型:设节点失效的实施速率为 λ,从失效状态到系统可用的修复实施速率为 μ。其中状态0表示系统不可用,状态1表示系统可用。图1给出了1个集群节点的CTMC。

图1 1个集群节点的CTMC

此CTMC模型PRISM建模如下:

对于一个集群节点来说,其可用性指的就是其长时间正常运行的稳态概率。PRISM工具通过使用时序逻辑语言,可以对这一属性进行描述如下所示:

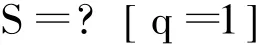
其含义:系统处于状态1(即可用状态)的稳态概率是多少？

我们假设lamda=600,mu=800,PRISM引擎采用枚举方法Power方法,验证得出其稳态概率

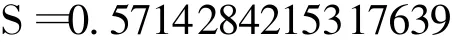
结果近似相等,说明我们的方法是非常正确、有效的。

通过进一步实验,假设此集群节点修复的速率μ(mu)一定,我们考查集群节点在不同失效速率下,整个集群节点系统可用的概率分布。

取mu=800,lamda初始值为100,最大值为10000,由初始值向最大值步进,步长假设为100,通过实验表明,当系统修复速率一定时,系统可用性随着系统失效速率的增大而降低。此实验的结果图如图2所示。

图2 一个集群节点系统失效速率对系统可用性影响分布图

4.2 2个集群节点的可用性的PRISM建模与验证

[1]文中,分析了由2个集群节点组成的渲染系统的情形,提出了 “单步修复”和整体修复”两种情形下CTMC。

假设每个节点的平均无故障运行时间(MTTF)为1/λ。当一个节点故障发生后,系统可以按概率c自动的恢复运行(称为被覆盖的故障),按概率1-c系统不能自动恢复(称为未被覆盖的故障)。被覆盖的故障可以通过一个短暂的系统重配置过程来恢复系统运行,设平均重配置时间是1/δ。一个未被覆盖的故障要重启系统来恢复运行,这将需要更长的时间,设平均重启时间为1/β(1/β＞1/δ)。无论在那种情况下,发生故障的节点都要进行修复,设平均修复时间为1/μ。在修复过程中,另一个节点继续运行并提供服务。如果修复期间另外一个节点也发生故障,则系统将不能提供服务,直到修复完成。

4.2.1 “单步修复”情形下的PRISM建模与验证

在单步修复模式下,2个集群节点可通过一定的实施速率从同时可用转变到同时失效的状态,然而,同时失效后只能采用“单步修复”的方式返回到同时可用的状态。如图3所示的2个集群节点在“单步修复”情形下的CTMC。

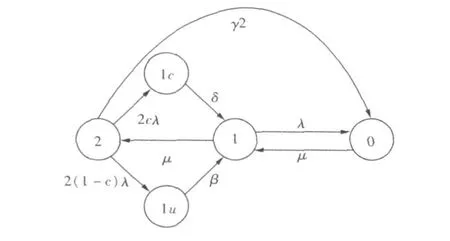
图3 2个集群节点在“单步修复”情形下的CTMC

如图3所示,两个集群节点通过实施速率 γ 2来实现同时失效。

此CTMC模型PRISM建模如下:

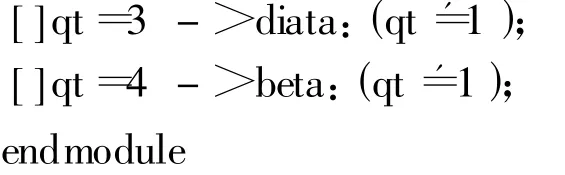
对于2个集群节点来说,其可用性指的就是其至少有一个节点是正常运行的稳态概率。PRISM工具通过使用时序逻辑语言,可以对这一属性进行描述如下所示:

S=？[qt！=0]

其含义:系统处于非状态0(即不可用状态)的稳态概率是多少？

为了更好地和[1]文中的结果进行比较,我们使用[1]中提供的相关参数,假设c=0.9,gama=0.0005,lamda=0.001,mu=2,diata=60,beta=12,PRISM引擎采用枚举方法Power方法,验证得出其稳态概率

S=0.999749760413066

[1]文中,结果显示系统的稳态可用性为0.9997031676,和我们的结果近似相等。

4.2.2 “整体修复”情形下的PRISM建模与验证

在整体修复模式下,当两个集群节点出现共模失效后,可以通过整体修复和复位操作实现两个集群节点的同时可用,即从状态“0”可以通过实施速率 θ 2转到状态“2”。如图4所示的2个集群节点在“整体修复”情形下的CTMC。

图4 2个集群节点在“整体修复”情形下的CTMC

此CTMC模型PRISM建模如下:

稳态概率属性描述如下所示:

同样,假设c=0.9,gama=0.0005,lamda=0.001,mu=2,diata=60,beta=12,PRISM引擎采用枚举方法Power方法,进一步假设thita=1,验证得出其稳态概率

[1]文中,结果显示系统的稳态可用性为0.9997885739,和我们的结果近似相等。

对比P1情形下系统的稳态可用性,可用性的增量值:

和[1]文中的增量值0.0000854063误差近似相等。

以1年365天来计算,这意味着在当前参数下,整体修复方案与单步修复方案相比,系统在稳态时可提供Web服务的平均时间提升了:365×24×60×0.0000834143299421=43.84257181756776约44分钟。

假设系统失效速率gama一定,整体修复速率thita在不同值的情况下,对系统可用性的影响如图5所示,整体修复速率越快,系统可用性越高。

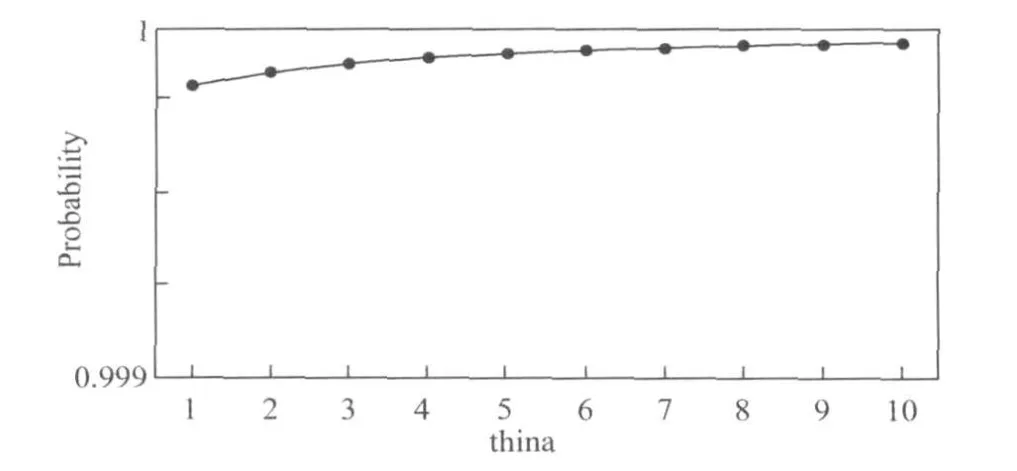
图5 “整体修复”集群节点可用性随修复速率变化分布图

4.3 特定的n(n＞2)个节点的PRISM建模与验证

同样地,我们可以对n(n＞2)个集群节点组成的渲染系统进行PRISM建模与验证。

[1]文中给出了n(n＞2)个集群节点的CTMC,如图6所示。

设渲染系统的总节点数为n,对于k个集群组成的而言,当其中的k(k∈(2,n])个集群节点同时出现共模失效的情形时,系统具有完全重启的自恢复功能,即经过一段时间后可以通过复位操作实现k个集群的重新同时可用。其中 γ i(i=2,…,n)表示i个集群节点发生整体失效的实施速率,θ j(j=2,…,n)表示j个集群节点通过整体恢复操作由失效状态转变为同时可用状态的实施速率。

这样通过假定节点数目 =2,3,4……就可以分别描述其PRISM模型,然后通过验证其长期的稳态概率属性:S=？[qt！=0],就可以得出其可用性概率,通过相关实验还可以得到相关的数据分析。

但是,这里就存在一个问题,当n值比较大时,我们在创建PRISM模型描述时,因为状态转移的增多,需要手写的代码描述迅速增多,这对于模型的描述来说,效率就很低下。这就是带参系统模型检查[4]的问题,如何解决对于任意n值的模型描述问题,PRISM工具好像并不支持带参模型检查,至少从我们得到的现有资料上并没有发现PRISM具有这一特性。

图6 n个集群节点的CTMC

5 结论和下一步工作

本文通过针对1个集群节点和2个集群节点组成的渲染集群系统,使用概率模型检查工具PRISM,对系统的可用性进行了分析,通过数据比对,证明我们的方法是正确有效的。但是当集群节点数目大量增加时,基于PRISM的建模手段受到了一定限制,针对这个问题,我们会进一步深入研究并采用合理的手段加以解决。

致谢

本文的研究工作受到国家863计划项目(2008AA01A318)、北京市自然科学基金(4112052)、中国传媒大学211工程重点学科建设三期项目、中国传媒大学2010年工科规划项目、广播电视总局高校科研项目的共同资助。

[1]洪志国.基于Markov过程的渲染集群可用性分析[J].通信学报.

[2]PRIS M manual.http://www.prismmodelchecker.org/manual/.

[3]MKwiatkowska,G Norman,D Parker.Stochastic model checking.In M Bernardo and J Hillston,Formal Methods for the Design of Computer[J].Communication and Software Systems:Performance Evaluation(SFM'07),volume 4486 of LNCS(Tutorial Volume),220-270,Springer,2007.

[4]T Arons,A Pnueli,S Ruah,Y Xu,L Zuck.Parameterized Verification with Automatically Computed Inductive Assertions[J].Computer Aided Verification,Lecture Notes in Computer Science,2001,Volume 2102/2001,221-234.

A Stochastic Model Checking Method for the Usability of Clusters about Distributed Rendering System

WANG Ke-min,WANG Yong-bin
(School of Computer,Communication University of China,Beijing 100024,China)

In order to study the usability of rendering clusters,we adopt in a Probabilistic Model checker-PRISM.We formalized a one-node cluster system and a two-node cluster system with PRISM language,and then through the property language and verification method,we get the steady-state probability about the usability.

stochastic model checking;rendering;PRISM;CTMC;CSL

TP301.6

A

1673-4793(2011)03-0034-06

2011-04-01

王克敏(1979-),男,中国传媒大学计算机学院讲师,在读博士.E-mail:bbi-wkm@cuc.edu.cn

(责任编辑

:龙学锋)