郑州市年降水量的ARIMA模型预测
刘德林
(河南理工大学 应急管理学院,河南 焦作 454000)
郑州市年降水量的ARIMA模型预测
刘德林
(河南理工大学 应急管理学院,河南 焦作 454000)
郑州市是我国严重缺水的城市之一。为掌握该市降水资源变化状况,提供区域水资源合理开发利用的依据,运用差分自回归滑动平均模型(ARIMA),在对郑州市1951-2008年降水量数据进行预处理、模式识别、参数估计与模型检验的基础上,建立了郑州市年降水量的ARIMA(2,1,2)预测模型。结果表明:该模型预测相对误差范围为-6.36%~0.49%,预测精度较高,可以用于该区未来降水量的短期预测。
郑州市;年降水量;ARIMA;预测
郑州市是中国严重缺水的城市之一,全市人均水资源量仅为198m3,不足河南人均的1/2及全国人均的1/10[1]。而作为自然界水循环重要环节的大气降水是该区水资源的主要补给来源,其大小决定着该区水资源的丰富程度[2]。因此,研究郑州市年降水量的变化趋势并对未来降水量进行合理预测,将有利于该区水资源的合理开发利用。然而,受下垫面性质与气象条件复杂多样及变异性的影响,降水过程存在着大量的随机性与不确定性,目前还难以通过物理成因来准确预测未来某一时段的降水量,同时传统的趋势外推预测模型也不适合该类时间序列数据的预测[3]。统计学家G.E.P.Box与G.M.Jenkins于20世纪70年代提出的差分自回归滑动平均模型(Auto-Regressive Integrated Moving Average Model,简称ARIMA)可用于非平稳时间数据序列的分析、预报与控制[4]。与平稳时间序列、周期时间序列模型相比,该建模方法在数学上更为完善,预测精度更高[5]。因此,本文以郑州市1951-2008年逐年降水量为基础,在对年降水序列进行平稳性和正态分布检验的基础上,通过模式识别、参数估计和模型检验等步骤,采用数据处理软件DPS 7.05经过多次拟合优选[6],建立郑州市年降水量预测精度较高的ARIMA(2,1,2)预测模型。
1 ARIMA模型简介
ARIMA建模的基本思路是假设所研究的时间序列是由某个随机过程产生的非平稳时间序列,对该非平稳时间序列数据进行若干次差分处理,使其变成平稳时间序列,然后用时间序列的观测值去建立该随机过程的自回归滑动平均模型,用所建立的最优模型进行预测。该模型共有3个参数,分别是自回归阶数(p)、差分次数(d)和滑动平均阶数(q),通常被记作ARIMA(p,d,q)。其通用表达式为:
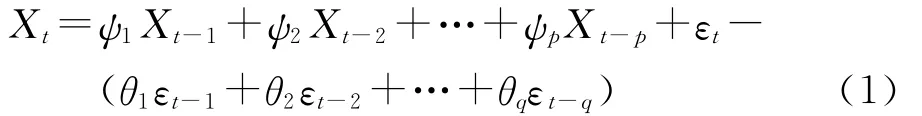
式中:Xt——研究的时间序列数据;ψ1,ψ2,…,ψp——自回归系数;p——自回归阶数;θ1,θ2,…,θq——滑动平均系数;q——滑动平均阶数;εt——白噪声序列。
该模型体现了对p阶自回归模型的误差εt进行q阶修正的预测思想。由于模型以多项和的形式出现,因此p,q伸缩自如,加之差分处理(d),使模型能适应于任何类型的时间数列[8]。运用ARIMA模型进行建模预测一般包括数据预处理、模式识别、参数估计和模型检验4个步骤。
(1)数据预处理。包括数据序列的正态性检验与差分平稳化处理,其主要目的是使时间序列数据满足建立ARIMA模型的前提条件,提高预测的精度。当时间序列正态检验的卡方值和Daniel检验的秩相关系数的p值大于0.05时,表明数据正态分布且处于平稳状态,反之亦然。
(2)模式识别。又称模型定阶,是ARIMA建模的关键。一般ARIMA(p,d,q)模型的定阶方法主要是依据样本自相关系数(ACF)与偏相关系数(PACF)的截尾性、拖尾性和周期性进行[5,7]。但因该模型结构复杂,AR部分的ACF和MA部分的ACF会相互影响,因此,本文采用从低阶 ARIMA(1,1,1)模型进行尝试,结合最小信息量AIC准则并考虑相关系数R及拟合度C的大小来确定模型的阶次。如果AIC值较小且R值及拟合度C值较大,则说明模型的拟合效果越好。AIC准则可定义为:
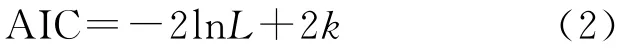
式中:L——模型的极大似然函数;k——模型的独立参数个数。
(3)参数估计。ARIMA模型的参数辨识采用麦夸特(Marquardt)非线性最小二乘法进行。
(4)模型检验。如果所建模型合适,根据定义,残差序列εt应为白噪声序列。因此,模型检验主要是残差序列的白噪声检验。由残差εt的样本自相关函数ρk(εt)构造box-pierce的修正统计量Q。
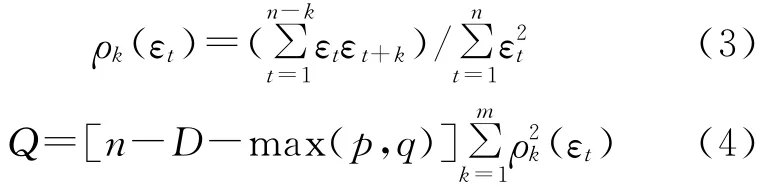
式中:ρk(εt)——残差εt的样本自相关函数;Q——统计量;n——样本容量;D——差分后损失的数据个数;m一般取N/4,k,εt符号含义同前。在一定显著性水平α(一般α取0.05或0.01)下,根据卡方分布表查得临界值χ2α(m-p-q),若Q≤χ2α(m-p-q),则认为模型是合适的,否则需要对模型的残差作进一步的识别或重新构造模型。
2 ARIMA模型的应用
2.1 数据来源与方法
从中国地面气候资料国际交换站郑州气象站和《河南统计年鉴》收集并计算郑州市1951-2008年逐年降水资料,利用1951-2005年的数据作为建模数据序列,2006-2008年数据作为模型检验序列,在DPS平台上进行ARIMA建模分析。
2.2 数据检验与处理
由正态性检验卡方值的显著水平(p=0.01<0.05)和Daniel检验结果的显著水平(p=0.035<α=0.05)可知,该时间序列呈非正态分布且处于非平稳状态,因此,须对数据进行转换或差分处理。对原始降水数据进行一阶差分后发现,降水时间序列卡方值的显著水平p=0.97>0.05且Daniel检验结果的显著水平p=0.363>0.05,表明差分后的降水时间序列已呈正态分布且处于平稳状态,达到ARIMA模型的建模要求。
2.3 ARIMA模型的参数估计和定阶
本文采用麦夸特非线性最小二乘法进行模型的参数估计。采用从低阶到高阶依次尝试的方法确定模型的阶次,取d=1,即模型为 ARIMA(p,1,q)。通过从低阶次到高阶次对p和q的不同取值分别进行拟合和参数估计,得到时间序列不同的ARIMA模型(表1)。根据AIC值越小、相关系数R值及拟合度C值越大模型拟合效果越好的原则,可发现较为理想的模型是 ARIMA(2,1,2)
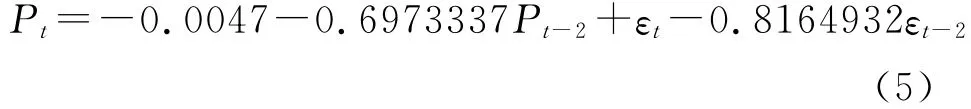
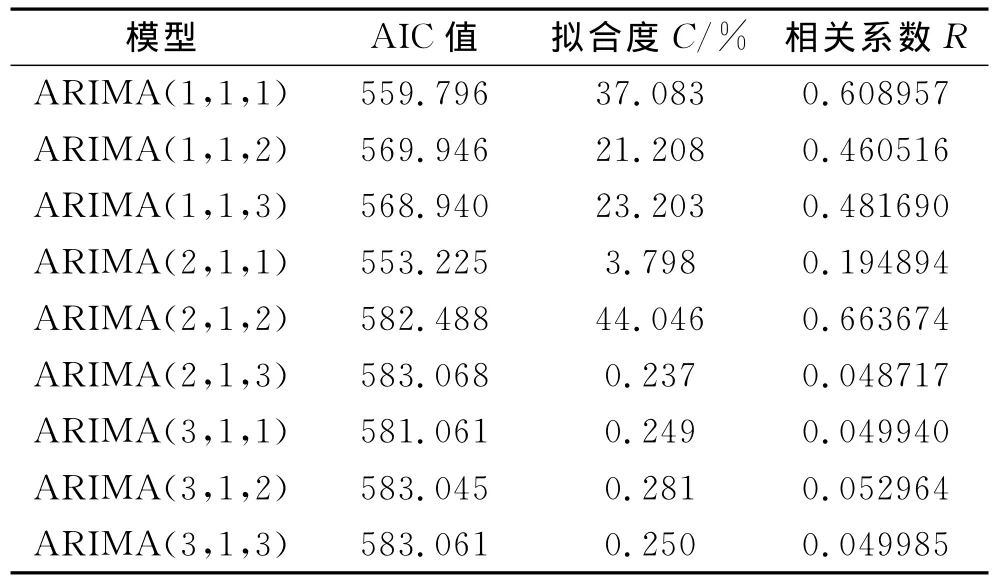
表1 ARIMA(p,1,q)模型判定指标
2.4 模型检验
对残差序列εt进行检验得Q=14.88。查自由度df=15,α=0.005时,χ2=32.8,可见残差序列的Q值远远小于显著水平0.005下的卡方值,说明残差序列εt在极显著水平下为白噪声,模型有效。同时,通过对郑州市2006-2008年降水量的预测值与实际值比较发现(表2),预测值与实际值差异较小,说明ARIMA(2,1,2)模型具有较高的预测精度,可用于郑州市年降水量的预测。此外,从拟合值与实测值的曲线图(图1)来看,模型预测值与实测值拟合较好,除在个别年份差异稍大外(如1953年和1968年),其他年份误差都很小,这也表明了模型拟合的结果是可靠的。
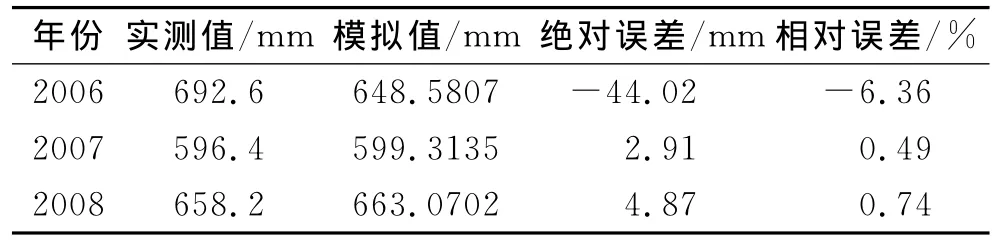
表2 郑州市降水模型ARIMA(2,1,2)预测精度分析
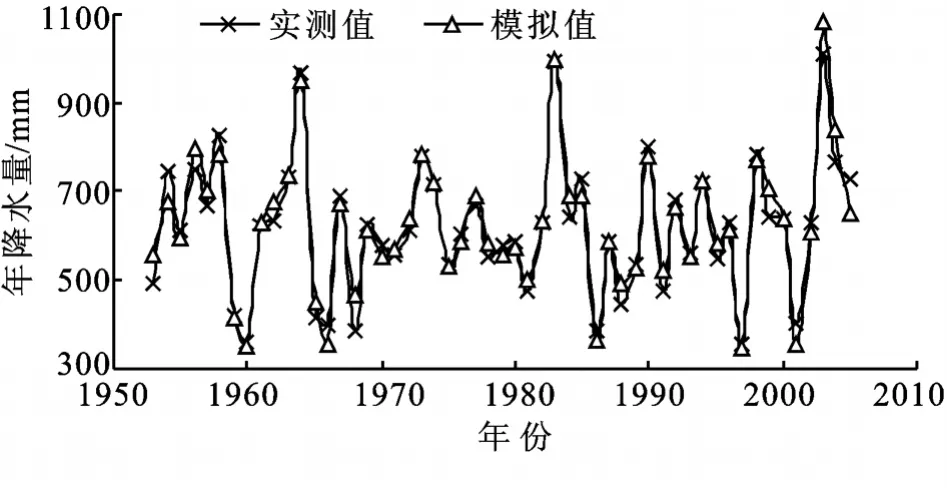
图1 郑州市年降水量模拟值和实测值比较
3 结论
通过对1951-2005年郑州市年降水量进行时间序列分析,在对数据进行预处理、模式识别、参数估计和模型检验的基础上,选择了 ARIMA(2,1,2)模型对郑州市年降水量进行模拟与预测。
(1)除在个别年份模拟值与实测值差异稍大外(如1953年和1968年),其他年份误差都很小,这说明该模型拟合效果较好、结果可靠。
(2)利用该模型对2006-2008年郑州市年降水量进行预测,预测值与实际值差异较小,相对误差基本控制在10%以内,说明 ARIMA(2,1,2)模型具有较高的预测精度,可用于郑州市年降水量的预测。
但考虑到降水是一个复杂多变的动态系统,受地区维度差异、气温变化、植被覆盖、流域分布等多因素的综合影响,该模型虽然对郑州市年降水的预测较为精确,但是否适用于其他地区,还有待进一步验证。
[1]李春晓.郑州市水资源极度短缺,人均占有量不足全国1/10[N].东方今报,2011-03-03(A10).
[2]王友贺,谷秀杰,师丽魁,等.郑州市降水特征分析与水资源问题初探[J].气象与环境科学,2007,30(3):61-64.
[3]张杰,刘小明,贺玉龙,等.ARIMA模型在交通事故预测中的应用[J].北京工业大学学报,2007,33(12):1295-1298.
[4]Box G E P,Jenkins G M.Time series analysis:Forecasting and control[M].San Francisco:San Francisco Press,1978.
[5]刘贤赵,邵金花.烟台地区降水量的ARIMA随机模型研究[J].数学的实践与认识,2006,6(8):8-12.
[6]唐启义,冯光明.DPS数据处理系统[M].北京:科学出版社,2007.
[7]卫小英,霍丽骊.博克思-詹金斯预测方法简介[J].预测,1984(Z1):35-39.
[8]赵亮,吴艳乔,雷海科,等.运用ARIMA模型对我国人均卫生费用的预测[J].现代预防医学,2010,7(3):410-412.
Annual Precipitation Forecasting of Zhengzhou City Based on ARIMA Model
LIU De-lin
(Emergency Management School,He'nan Polytechnic University,Jiaozuo,He'nan454000,China)
Zhengzhou City is one of serious water shortage cities in China.In order to realize the change state of precipitation,and to provide the basis for the rational development and utilization of water resources,we applied ARIMA model to establish the ARIMA (2,1,2)model for the annual precipitation forecasting of Zhengzhou City.Some works including the data preprocessing,pattern recognition,parameter estimation and model checking have been done before the establishment of this model.The results showed that the forecast of ARIMA(2,1,2)model is exact,the relative error ranges from -6.36%to 0.49%.The model can be used for short-term forecast of annual precipitation.
Zhengzhou City;annual precipitation;ARIMA;forecasting
P333.6
A
1005-3409(2011)06-0249-03
2011-04-24
2011-05-12
河南省教育厅自然科学基金(2009A170003);河南理工大学博士基金(B2011-033);河南省政府决策研究招标课题(2011B231)
刘德林(1979-),男,山东潍坊人,博士,讲师,主要从事水土资源高效利用与应急管理方面的研究与工作。E-mail:liudelina@163.com

