基于ADRC和反步法的PMSM位置控制系统

侯利民，任志玲，王 巍，李秀菊

(辽宁工程技术大学，辽宁葫芦岛125105)

0 引 言

交流位置控制系统追求的性能指标是定位的快速性、准确性和无超调，同样也是PMSM位置控制系统追求的目标。由于PMSM是一个多变量、强耦合、非线性、变参数的复杂对象，位置控制系统的性能容易受到电机参数变化和负载扰动等不确定因素的影响，因此要获得高性能指标、宽调速范围的永磁同步电机位置控制系统，必须研究先进的非线性控制策略与手段，使系统具有较强的动态响应、自适应性和抗干扰能力。目前一些控制策略已经相继提出，如:自适应反步控制［1－4］、自抗扰控制［5－9］、自适应逆控制、滑模变结构控制［10－11］、无源控制［12］等，这些方法都有各自的优缺点，仅依靠单一的控制方法还很难得到理想的控制效果，需要将一些控制方法结合在一起，互相取长补短，形成交叉综合的控制技术。

PMSM位置控制系统的结构通常有两种:一种是位置外环、电流内环的双环结构，省掉了速度闭环［13］;另一种是由位置环、速度环、电流环组成的三环结构。双环系统研究的重点是要求系统位置响应的动态性能，而对速度调节的性能要求并不高，适合于点对点运动控制场合。而三环位置控制系统是目前被普遍认同的位置控制系统结构，其中的速度控制要求精度也是很高的，适合于轨迹运动控制场合。文献［5］的位置外环控制器采用二阶ADRC方法构造，电流环采用PI调节器，共同组建了双环位置控制系统，其中位置环的二阶状态方程认为存在已知项f0(x1，x2)，但通常粘性摩擦系数也是变化的。文献［7］的位置外环控制器采用一阶ADRC方法构造，而速度环和电流环均采用传统的PI控制器，位置跟踪精度高，动态响应快，基本消除了位置跟踪“平顶”现象，但当系统参数变化和受扰动时，由于内环采用PI控制器，导致鲁棒性减弱，速度过渡不平滑。文献［14－15］将Back Stepping方法应用于永磁同步电机位置伺服系统控制器的设计，但当系统参数变化时，位置的快速跟踪就很难保证。文献［16－17］将自适应Back Stepping方法应用于具有不确定参数的永磁同步电机速度跟踪控制中，保证在系统参数变化时系统速度快速跟踪，但需要实时估计定子电阻、粘性摩擦系数和负载的变化。

本文按照双环控制结构的理念设计了三环位置控制系统，对于三环系统中的位置外环采用一阶系统的自抗扰控制策略得到期望的转速信号，利用反步法实现了速度的渐近跟踪，得到期望的q轴电流，然后逐步设计，得到系统的实际控制ud、uq，通过自适应方法估计负载的变化。仿真表明系统的动态响应快，稳态精度高，无超调，速度平稳光滑，控制系统具有较强的鲁棒性。

1 一阶位置外环的ADRC设计

永磁同步电机的转子位置和速度之间的表达式:

永磁同步电机位置控制系统的高性能指标易受负载扰动、电机参数变化等因素的影响，虽然这些扰动(a(t))找不出精确的数学模型，但它确实存在于位置环之中，成为转子位置和速度之间的表达式中的一部分［5］，如下:

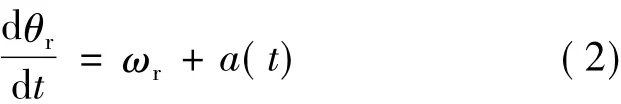
这样就可以利用自抗扰控制器原理，通过扩张状态观测器(ESO)估计出未知的a(t)并进行前馈补偿，那么式(2)就可以变换为一个一阶线性模型。因此，位置环的一阶自抗扰控制器表达式:

一阶跟踪－微分器为:

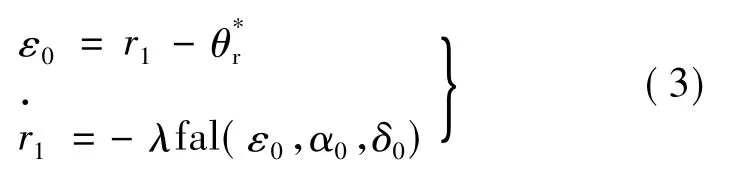
二阶扩张观测器:

非线性反馈控制律:

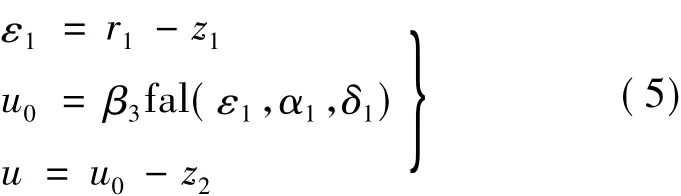
2 自适应反步法速度控制器和电流控制器的设计

根据永磁同步电机同步旋转d－q坐标系下的数学模型，控制目标设为速度跟踪，则跟踪误差:

选择e为虚拟状态变量，构成子系统，系统方程:

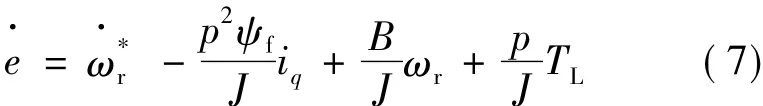
为了使速度跟踪误差趋于零，对于子系统构造如下Lyapunov函数:

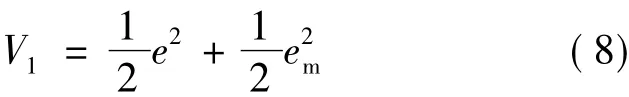
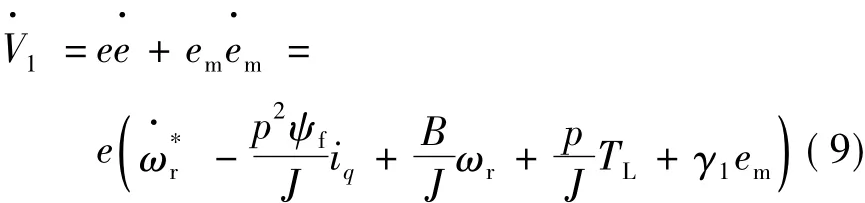
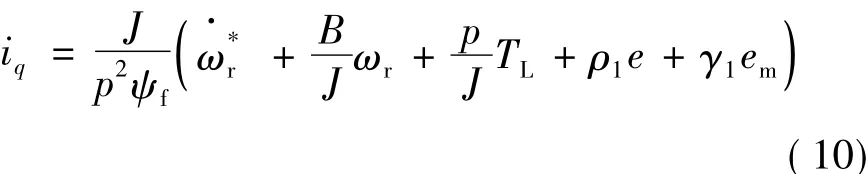
式中:ρ1＞0，则可以使式(9)变为:

因此控制式(10)，则可达到速度全局渐近跟踪的目的。

为了实现PMSM的完全解耦和速度跟踪，可以选择参考电流:

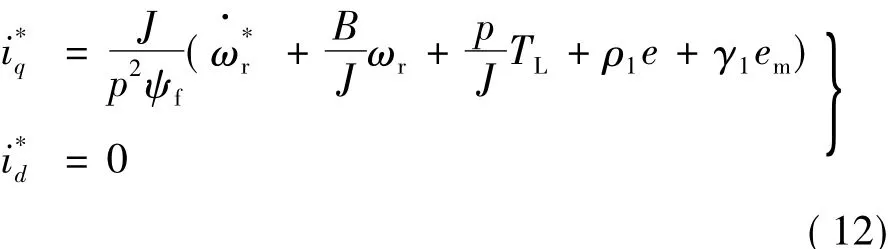
考虑负载转矩在电机运行过程中会发生变化，定义:

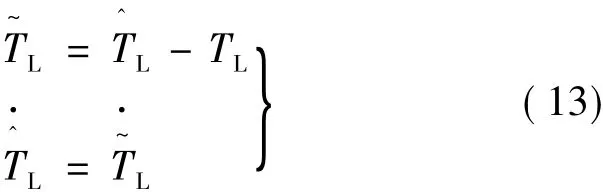
选取如下参考电流:

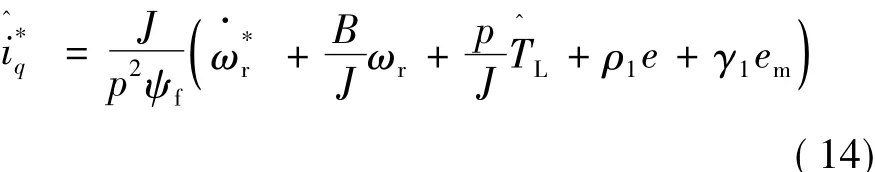
将式(14)代入式(7)得:

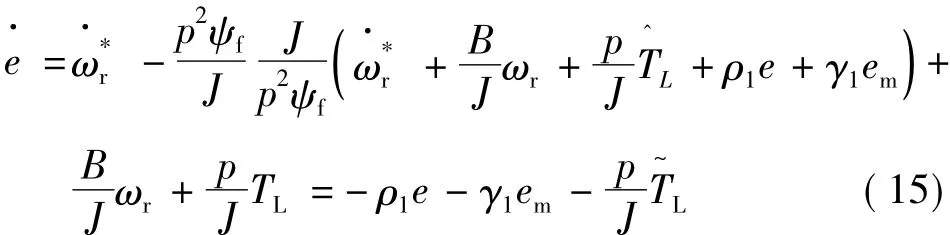
为了实现电流跟踪，选择电流跟踪误差为虚拟误差变量:

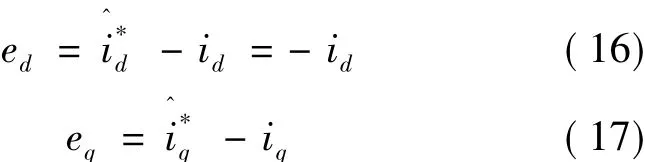
由e、ed、eq可以组成新的系统。

分别对式(16)、式(17)求导得:

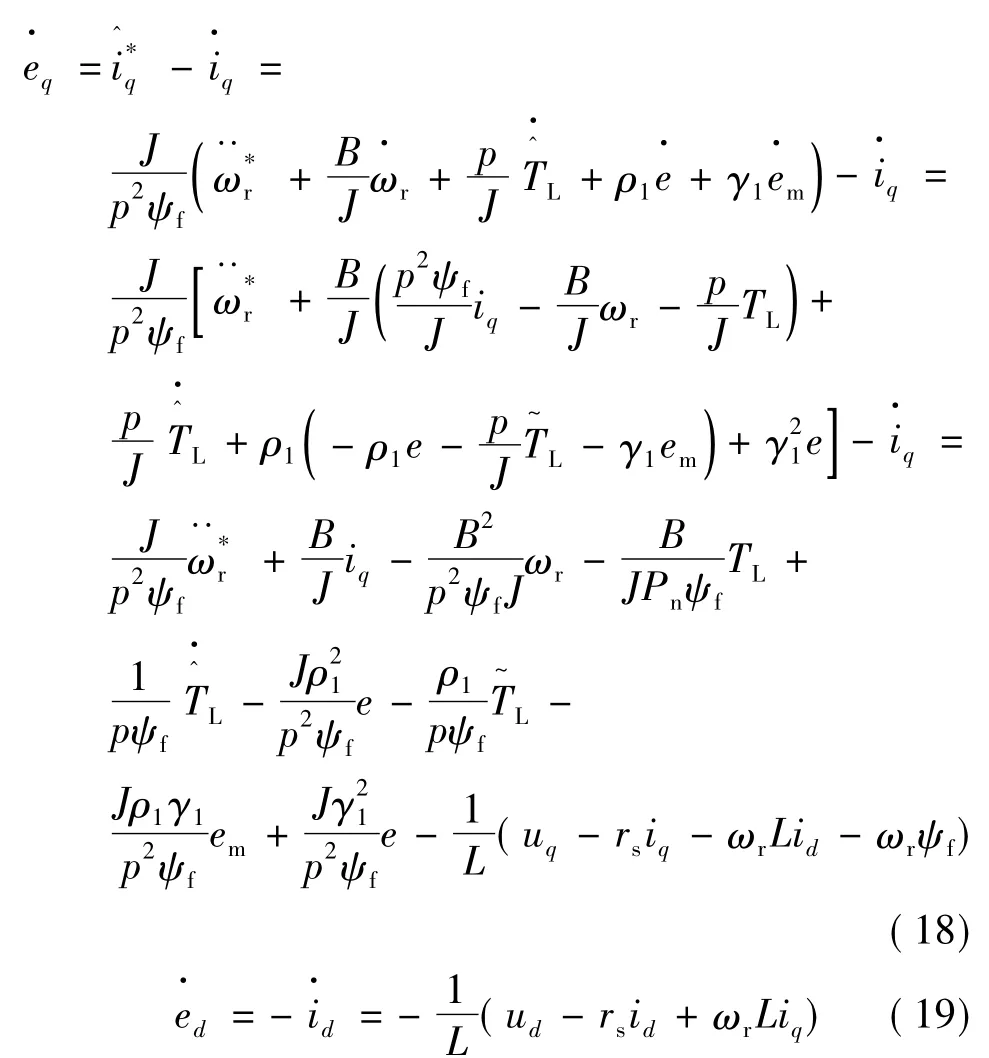
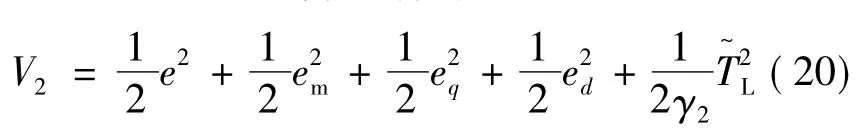
式中:γ2＞0，对式(20)求导得:

对于新的子系统构造新的Lyapunov函数:

式中:ρ2＞，ρ3＞0。选择自适应律:

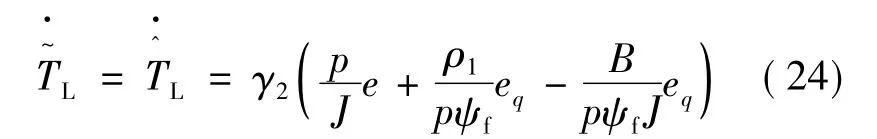
将式(22)～式(24)代入式(21)得:

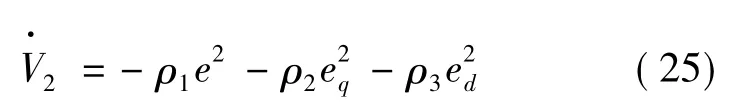
式(14)和式(22)、式(23)构成了速度控制器和电流控制器。整个三环位置控制系统的结构框图如图1所示。

图1 三环位置控制系统的结构框图

3 仿真结果

为了验证三环位置控制系统的性能，对此控制系统进行了仿真研究。PMSM电机仿真参数如下:rs=1.6 Ω，Ld=Lq=0.006 365 H，ψf=0.185 2 Wb，Pn=2，J=0.000 185 4 kg·m2。仿真实验结果如图2～图11所示。

转子位置给定信号按2sin4πt规律变化，位置跟踪/误差和速度曲线如图2～图4所示。

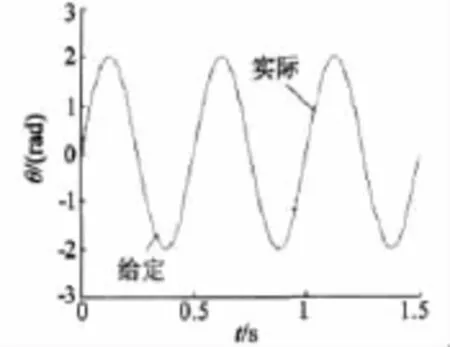
图2 转子位置跟踪

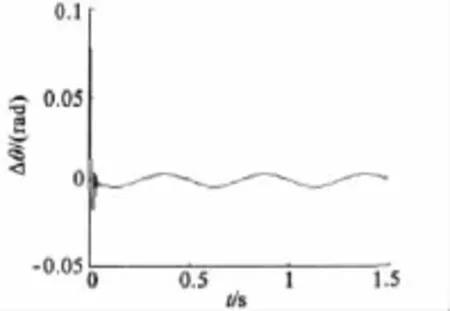
图3 转子位置跟踪误差

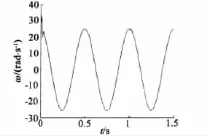
图4 转子速度

从仿真结果来看，初始时位置跟踪误差最大为0.076 rad，最小为－0.015 rad，随后很快进入稳态跟踪，误差在±0.003 8 rad之间，可见位置跟踪精度较高，响应快，并且PMSM速度平稳。

转子位置给定信号按2sin4πt规律变化，在0.1 s突加负载5 N·m，在0.2 s突卸负载，位置局部跟踪/误差和速度曲线如图5～图7所示。

从仿真结果来看，突加/减负载时，转子位置有±0.05 rad的波动，随后进入稳态跟踪，误差在±0.003 8 rad之间，能很快跟踪给定位置信号，PMSM转速在加/减负载时有些波动，很快趋于平稳光滑。

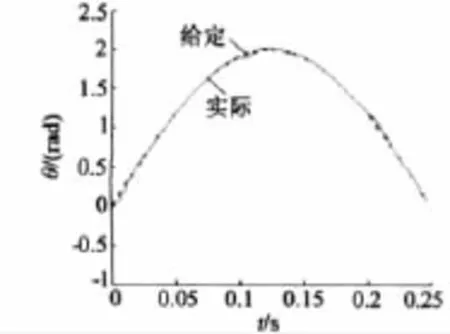
图5 转子位置跟踪

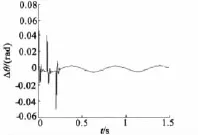
图6 转子位置跟踪误差

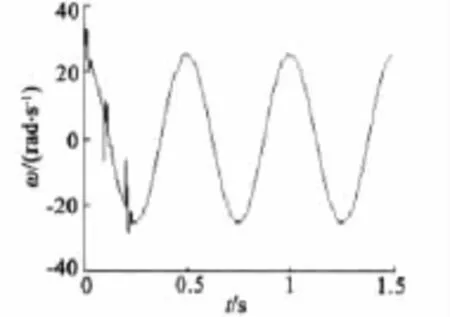
图7 转子速度

转子位置给定阶跃信号为2 rad，空载情况下位置跟踪和速度曲线如图8～图9所示。转子位置给定斜坡信号为2 rad，在0.7 s突加负载5 N·m，电阻变化2倍，粘性摩擦系数变化5倍，在0.9 s突卸负载情况下位置跟踪和速度曲线如图10～图11所示。

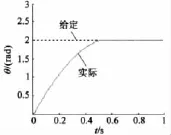
图8 空载下转子位置跟踪

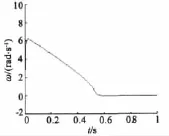
图9 空载下转子速度

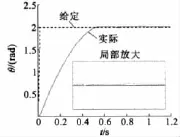
图10 加减载时转子位置跟踪

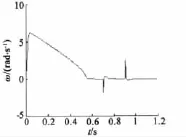
图11 加减载时转子速度

从仿真结果来看，转子位置在0.55 s跟踪给定值，稳态误差为零，速度为零。加减载时位置跟踪误差在 ±0.02 rad 之间，速度波动在 ±2.8 rad/s，随后趋于零。可见控制系统的响应较快，无超调，位置跟踪精度较高，抗参数变化和负载扰动能力较强。

4 结 语

本文针对PMSM位置控制系统追求定位的快速性、准确性和无超调的目标要求，以及系统鲁棒性的要求，设计了一种新颖的三环位置控制系统，即三环系统中的位置外环采用一阶系统的自抗扰控制策略得到期望的转速信号，利用自适应反步法实现了速度的渐近跟踪，得到期望的q轴电流，然后逐步设计，得到系统的实际控制ud、uq，通过自适应法估计负载的变化。该策略借助于一阶系统的自抗扰控制器进行模型不确定性估计并进行前馈补偿，与传统的自适应反步法相比，在系统具有较强的鲁棒性的同时，减少了参数的估计。仿真表明，系统的动态响应较快，稳态精度高，无超调，速度平稳光滑，对参数和负载的变化具有较强的鲁棒性。

［1]Ke SS，Lin JS.Sensorless Speed Tracking Control with Backstepping Design Scheme for Permanent Magnet Synchronous Motors［C］//Proceedings of the2005 IEEE Conference on Control Applications.Toronto，Canada，2005:487－492.

［2]March P，Turner M C.Anti－Windup Compensator Designs for Nonsalient Permanent－Magnet Synchronous Motor Speed Regulators［J］.IEEE Transactions on Industry Applications，2009，45(5):1598－1609.

［3]张兴华.永磁同步电机的模型参考自适应反步控制［J］.控制与决策，2008，23(3):341－345.

［4]Lin CH，Lin CP.Adaptive backstepping FNN control for a permanent magnet synchronous motor drive［C］//ICIEA，4th IEEE Conference.Xian，China，2009:2712－2717.

［5]孙凯，许镇琳.基于自抗扰控制器的永磁同步电机位置控制系统［J］.中国电机工程学报，2007，27(15):43－46.

［6]韩京清.自抗扰控制器及其应用［J］.控制与决策，1998，13(1):19－23.

［7]孙凯.自抗扰控制策略在永磁同步电机控制系统中的应用研究与实现［D］.天津大学，2007.

［8]邵立伟，廖晓钟，张宇河.自抗扰控制在永磁同步电机无速度传感器调速系统的应用［J］.电工技术学报，2006，21(6):35－39.

［9]Su Y X，Zheng C H，Duan B Y.Automatic disturbance rejection controller for precise motion control of permanent－magnet synchronous motors［J］.IEEE Transactions on Industry Electronics，2005，52(3):814－823.

［10]方斯琛，周波.滑模控制的永磁同步电机伺服系统一体化设计［J］.中国电机工程学报，2009，29(3):96－101.

［11]侯利民，张化光，刘秀翀.自适应模糊滑模软切换的PMSM无速度传感器鲁棒无源控制［J］.控制与决策，2010，25(5):686－690.

［12]裘君，赵光宙，齐冬莲.基于反馈耗散方法的永磁同步电机最大转矩/电流控制［J］.煤炭学报，2009，34(9):1285－1290.

［13]滕福林，胡育文，刘洋.位置/电流两环结构位置伺服系统的跟随性能［J］.中国电机工程学报，2009，24(10):40－46.

［14]王家军，赵光宙，齐冬莲.基于反推的永磁同步电机控制系统的位置跟踪控制［J］.电路与系统学报，2004，9(6):19－21.

［15]Ouassaid M，Cherkaoui M，Maaroufi M.Improved Nonlinear Velocity Tracking Control for Synchronous Motor Drive Using Backstepping Design Strategy［C］//Power Tech.，IEEE Conferences.Petersburg，Russia，2005:1－6.

［16]王家军，王建中，马国进.自适应Backstepping在永磁同步电机速度跟踪控制中的应用［J］.电气传动，2006，36(9):20－22.

［17]Tan Y L，Chang J，Tan H L.Adaptive backstepping control and friction compensation for AC servo with inertia and load uncertainties［J］.IEEE Trans.on Industrial Electronics，2003，50(10):944－952.