一种高精度FOA估计方法

何 兵,刘 刚,赵鹏涛,高 江,王 虹

(1.第二炮兵工程学院,陕西西安710025;2.第二炮兵青州士官学校,山东青州262500)

0 引言

频率估计不仅在理论上,而且在实际应用中,都有着非常重要的研究价值。利用信号FOA进行定位是确定发射源位置的基本和主要手段,其定位精度直接与TOA和FOA估计的准确度高度相关,因此,寻求一种精度高、计算简单、抗噪能力强的FOA估计算法一直是信号处理领域研究的热点问题。

自从20世纪30年代以来,由于在战争中雷达和声纳技术的广泛应用,使人们开始注意到信号频率估计问题研究的重要性,从20世纪60年代初,开始了更为广泛的研究。1958年由Blackman和Turkey提出的取样自相关法,是当时的一种流行的计算功率谱的方法。1965年由Cooley和Turkey完善了著名的FFT算法,把离散傅里叶变换的计算量减少了2个数量级,并且产生了一种称为周期图的谱估计方法,这种方法使谱估计由理论走向实用。1967年,Burg提出了最大熵谱估计方法。1968年,Parzen提出了自回归谱估计方法。1973年,由Pisareko提出的谐波分解方法提供了可靠的频率估计方法,而在1979年,Schmidt提出了谱估计的多信号分类算法,对于正弦波分量频率估计很有效,自此以后,有关特征分解法的频率估计有了广泛的研究。Rife[1]提出了利用正弦信号FFT主瓣内2条谱线的幅度的变化提高正弦信号的频率和幅度估计精度的方法。Jian等进一步研究了这种方法并提出了插值FFT正弦信号参数估计方法,这种方法既保留了基于FFT的正弦信号参数估计方法速度快的特点又提高了估计精度。Kay等人在文献[2]提出了一种高精度的频率估计方法,但受信噪比门限值影响。在文献[3]中,比较给出了6种FOA估计方法的优劣,FFT方法估计精度受到采样点的限制,周期图方法是无偏非零方差渐进估计器估计,最小方差法和归一化最小方差法是无偏最小方差频率估计器,Burg方法具有较高的频率分辨率,但应用于短时数据,会出现虚假峰值,MUSIC算法具有较高的分辨率,但是计算量较大。同时文献[4]用自相关函数和三阶累计量相结合提出了非高斯有色噪声中的正弦信号频率估计,该方法具有良好的频率估计性能。文献[5]提出了一种低信噪比下的正弦频率估计算法。文献[6]中提出了一种利用DFT频谱的相位和频率插值的综合算法提高频率测量精度的方法,但是存在相位模糊问题。齐国清等人在文献[7]中分别提出了加窗插值FFT频率估计方法和基于DFT相位的正弦波频率估计方法,利用分段DFT消除了相位测量中的正周模糊问题,在信噪比大于6 dB,采样点位1 024时,频率估计均方根误差约为DFT频率分辨率的1%。

总之,基于离散傅里叶变换DFT的频率估计方法运算速度快,但是估计精度受到信号时长的限制,一般只利用DFT实现频率的粗测,而利用MUSIC算法,AR模型算法以及最大似然估计算法等现代谱估计方法,可以对正弦信号频率进行精确估计,但是由于算法复杂,计算量大,难以实时处理而限制了进一步应用。针对通信信号瞬时到达频率估计问题,在借鉴和参考上述文献的基础上,通过对比仿真,选择了文献[2]中的频率估计方法作为单频复正弦信号的频率估计方法,然后提出了适用于数字调制信号瞬时到达频率估计的分段Kay频率估计方法,仿真结果显示该方法能够达到极高的估计精度,频率估计的标准差小于0.1 Hz。

1 信号模型描述

通常接收到的信号包括3个不同的部分:导频段(Tone)、导头段(Preamble)和数据段(Data)。导频段是一段长度为T1的未调制纯载波段,导头段为一段固定长度为T2的已知数据,其目的是为了进行位同步。数据段为一段特别编码的数据,长度为T3,包含发射源的相关信息,例如信号种类、国家号码等。

信号模型假设如下,信号的纯载波段定义如下:s(t)=acos(2πfct+θ),此处a代表信号幅度,fc为信号载波频率,θ是初始相位。数据段采用二相曼彻斯特编码,在相位调制中,数据“0”和数据“1”分别由表示为:

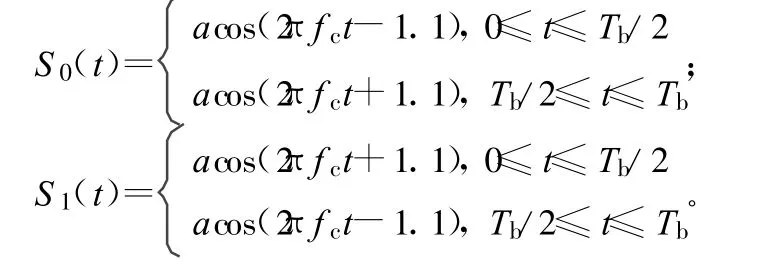
则调制信号表示为:

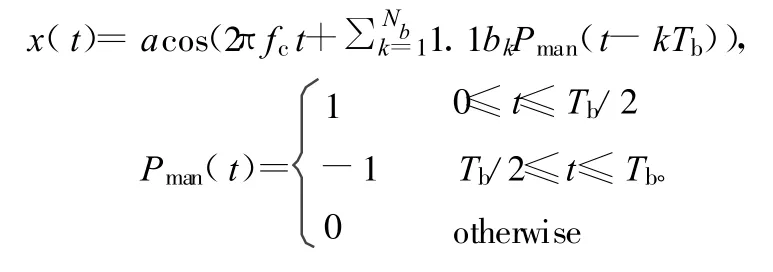
式中,bk=±1是信号发射的数据;Nb为信号长度,Tb为一个码元周期,Tb=2.5 ms;Pman(t)表示编码方式。编码使得信号频谱产生了较多的旁瓣,这对利用信号频谱峰值最大值进行频率估计带来干扰。信标信号信息时长为440 ms,上行中心频率为406MHz,码速率为400 bps。

2 Kay频率估计算法描述

假设接收的数据是一个有限的序列,即对数据进行了截断,相当于对数据加了矩形窗。在利用FFT算法进行频率估计时,存在着一个频率分辨率的限制,其分辨率的大小与数据的长度存在着反比关系。为了克服上述问题的影响,这里采用了一种基于相位差分的新算法,即Kay方法[2],该方法能够获得最大似然估计器的估计性能,且计算量较小,算法描述如下。

假设信号的模型如下:

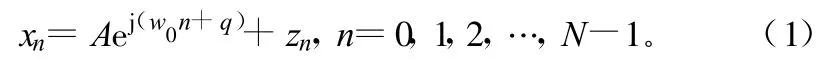
式中,A为信号的幅值;w0为信号的频率;θ为信号的初始相位,为一确定的未知量;信号频率w0为要求的估计量;噪声为zn=z1n+jz2n,z1n,z2n分别为实的均值为0;方差为 σ2/2的高斯白噪声(σ2是噪声zn的方差),并且z1n,z2n之间是不相关的。假设信噪比比较大,从而式(1)可用式(2)代替:

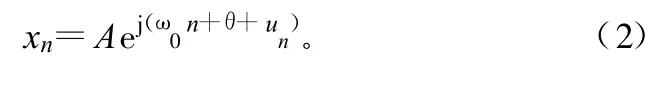
用∠x表示信号的xt的瞬时相位,则n时刻的相位为:∠xn=ω0n+θ+un,相位差分为:

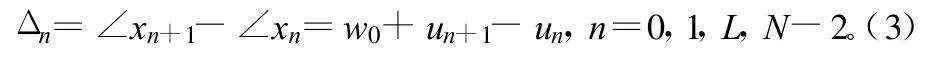
由式(3)可以看出,现在的问题转化为估计一个色高斯随机过程的均值 ω0。由式(3)可知,Δn是一个驱动噪声方差为σ2/2A2,系数为b0=1,b1=-1的实的滑动平均(MA)过程。式(3)所表示的线性模型的最小方差无偏估计即等价于 ω0的最大似然估计,并且可以通过最小化式(4)得到。

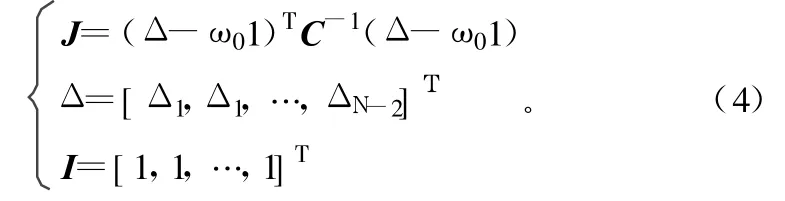
C是序列Δn的(N-1)×(N-1)的协方差矩阵式(4)的解为:

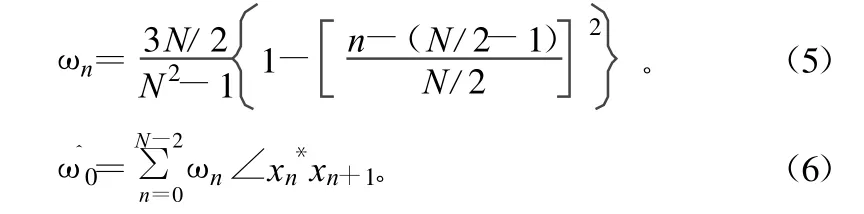
该估计器的方差为:

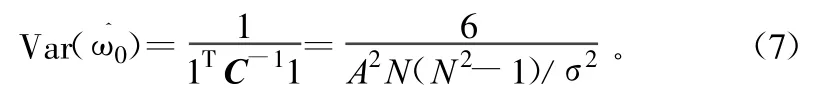
该估计器的方差达到了克拉美劳下界,是有效估计。

将Kay算法和其他几种算法,比如频率细化算法,Rife算法,修正FFT算法,MUSIC算法进行对比。分别比较几种算法随信噪比的增加估计偏差的变化情况,随载波频率变化估计偏差的变化情况以及随信号长度改变估计误差的比较。仿真结果如图1和图2所示。从图1仿真结果可以看出,Kay算法的估计精度要好于其他算法;从图2的仿真结果可以得出结论,Kay和频率细化算法估计精度基本不受载波频率变化的影响。通过综合比较,Kay算法是一种性能优良的单频复正弦信号频率估计方法。

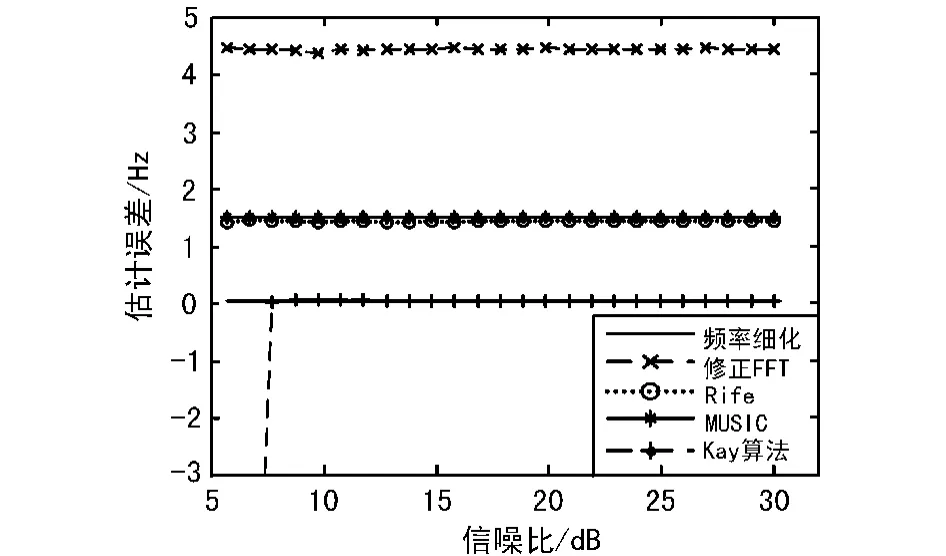
图1 随信号信噪比变化估计误差比较

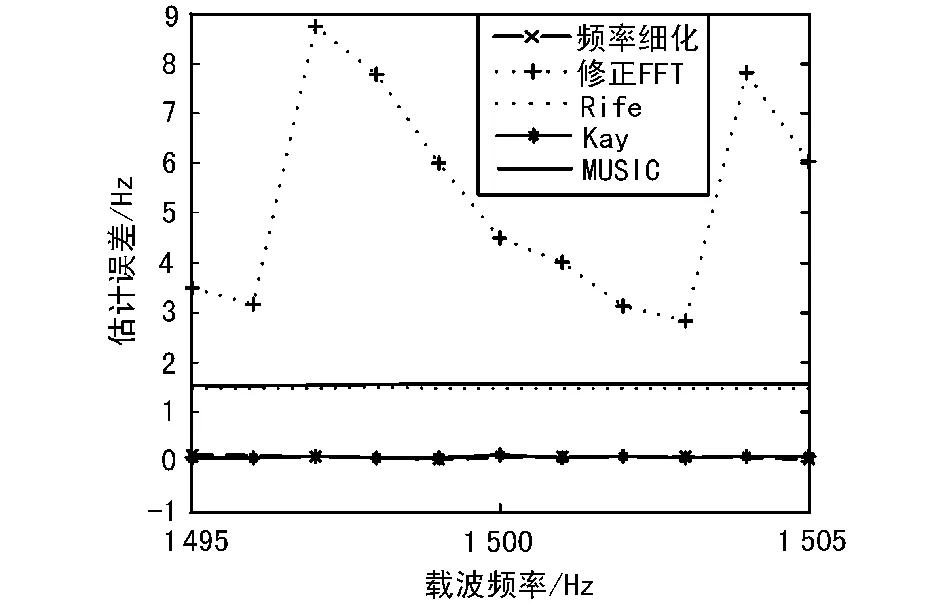
图2 随信号载波频率变化估计误差比较

3 分段Kay频率估计方法

通常对数字调制信号到达频率估计要求估计的是信号在某个特定数据上升沿或下降沿处瞬时频率,上述信号格式中的导头段(一段固定长度已知数据)就是为此而设计的。因此,问题转化为对导头段某比特上升沿或下降沿到达频率的估计。

由于在一个信号周期内,相对位置的运动导致多普勒频移存在,信号频率一直处在变化中,因此,利用单一复正弦频率估计方法不可取。针对上述接收信号模型,通过计算,在30 ms内多普勒频移量很小,认为在30 ms内信号频率为一常量,可视为一段单一复正弦频率信号。因此,这里提出可将整个接收数据段划分为时长为30 ms的子段,并且子段之间的数据有一定的重合,利用Kay算法估计各子段的频率,然后对估计出的频率进行曲线拟合,得到信号的时频分布图,从而求出接收信号某比特下降沿处的瞬时频率,称该方法为分段Kay频率估计方法。由于Kay算法存在着信噪比门限,因此,在频率估计之前须对接收信号进行下变频和滤波处理,以获得Kay算法门限值以上的信噪比。

以上述接收信号为模型,假设经过下变频处理和滤波后的信号模型为:x(n)=Acos(2p(fc+a×t)t)+n(t),a=0.5,表示信号的频率变化率,n(t)为噪声,信号长度为440 ms,信噪比为6 dB,载波频率为1 500Hz,估计其22 bit下降沿处的瞬时频率,即信号时长为220ms处的频率。通过计算机仿真,某次估计结果如图3所示,图3中实线是真实频率变化,虚线是估计的频率变化值,图中间似星星的点是瞬时频率估计值。从图3中可见,估计误差小于0.1 Hz。

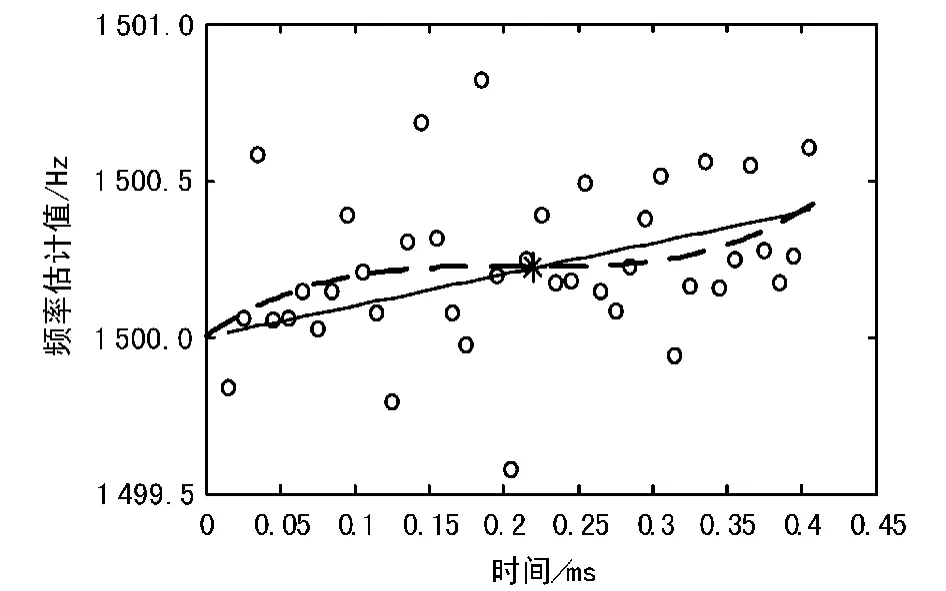
图3 基于分段Kay的频率估计

通过对上述过程经过100次的仿真计算,得到瞬时频率估计偏差均值为0.043 4 Hz,标准差为0.025 5Hz,达到了高精度的频率估计效果。

4 结束语

针对信号到达频率估计这个传统问题,设计了一般性的信号模型,针对该信号,通过比较选择了一种高精度的单频信号频率估计算法,并设计了信号到达频率估计的高精度估计方法—分段Kay频率估计,最后通过仿真试验,验证了频率估计的偏差小于0.1 Hz,精度较高。该方法计算量小,容易实现,具有极高的准确度和稳定性,具有较高的实用价值,对解决类似问题具有一定的借鉴意义。

[1]RIFE D C.Single-tone Parameter Estimation from Discrete-time Observations[J].IEEE Trans.Inf.Theory,1974(20):591-598.

[2]KAY.A Fast and Accurate Single Frequency Estimator[J].IEEE Trans.Acoust.Speech Signal Process.,1989(37):1987-1990.

[3]GOMEZ P C.Design of Local User Terminals for Search and RescueSystemswith MEO Satellites[M].Noordwijk:ProceedingsNAVITEC,The Netherlands,2004.

[4]梁应敞,王树勋,戴逸松.非高斯有色噪声中的正弦信号频率估计[J].电子学报,1995,23(4):111-114.

[5]陈光化,曹家麟.应用自适应时频分布的瞬时频率估计[J].系统工程与电子技术,2002,24(1):31-33.

[6]刘 渝.快速高精度正弦波频率估计综合算法[J].电子学报,1999,27(6):126-128.

[7]齐国清,贾欣乐.基于DFT相位的正弦波频率和初相的高精度估计方法[J].电子学报,2001,29(9):1164-1167.