一种高精度单频信号频率估计算法

刘建林,陈 兵

(中国电子科技集团公司第五十四研究所,河北石家庄050081)

0 引言

频率估计是信号参数估计中的经典问题,目前国内外已经提出了不少方法,其估计方法主要分为以自回归法等典型方法的参数估计[1]和以周期图法等典型方法的非参数估计[2,3]2类。短数据、高精度的快速频率估计是倍受电子战领域专家学者的关注。文章提出了一种先利用峰值前后3个DFT系数得到频率修正项的初值,再迭代计算修正后峰值前后位置DFT系数来得到频率修正项的精细值的频率估计新算法。仿真分析验证了算法能够快速、高精度估计单频信号的频率,比常规插值迭代算法所需迭代次数要少,有利于工程实现。

1 频率估计算法

1.1 信号模型

假设离散复单频信号模型为:

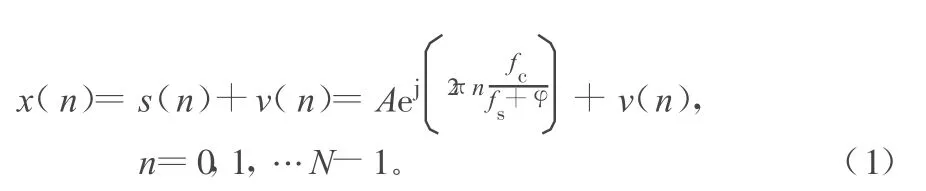
式中,A、fc和 φ分别为复信号的幅度、载频和初相;v(n)为零均值,方差为σ2的加性高斯白噪声;fs为采样频率;N为信号长度。

1.2 初值估计

信号的DFT系数为:

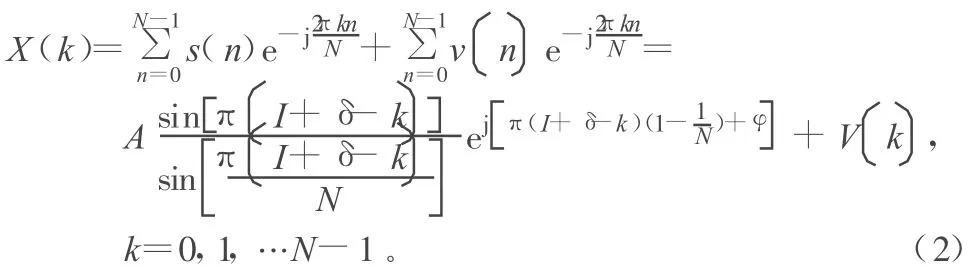
式中,I为幅度谱的峰值位置;δ为信号真实峰值位置与I的偏差值,即,且有为噪声的DFT系数。

暂不考虑噪声影响,且N较大时,I-1、I和I+1处的幅度谱可推导得到:

当|X(I+1)|＞|X(I-1)|时,即0＜δ≤0.5,信号真实频率位于I和I+1之间,有

式中,^δ0为估计出来的频率修正项初值。

1.3 迭代计算

考虑I-0.5、I+0.5两个位置,迭代计算DFT系数为:

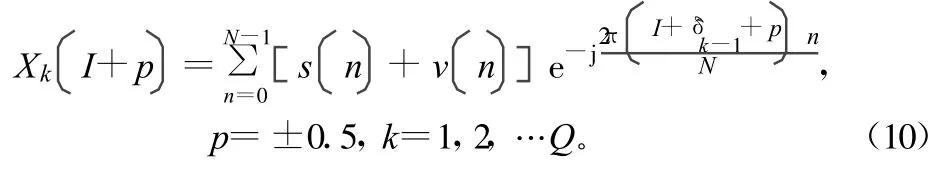
式中,k为迭代次数;^δk为第k次迭代后的频率修正项 ,有 ^δk=^δk-1+h(^δk-1),且h(^δk-1)的表达式[4]为:

^δ0的值按上节计算得到,但在文献[4]中频率修正项初值 ^δ0=0 。

2 仿真分析

2.1 算法收敛与迭代次数

仿真参数设置如下:采样频率fs=51.2 MHz,信号长度N=512,信噪比SNR=0 dB,信号幅度A=1,初相 φ=π/4,频率fc取值 12.75 MHz:0.01 MHz:12.85MHz,即对应FFT后峰值位置与信号真实位置偏差值 δ∈[-0.5,0.5],每个频点上做10 000次Monte-Carlo试验。在频率修正项初值 ^δ0为零和不为零(按1.2节分析计算)时,不同迭代次数Q与算法收敛性之间关系的性能曲线如图1所示。定义比值=测频均方误差(MSE)/克拉默界(CRB)。

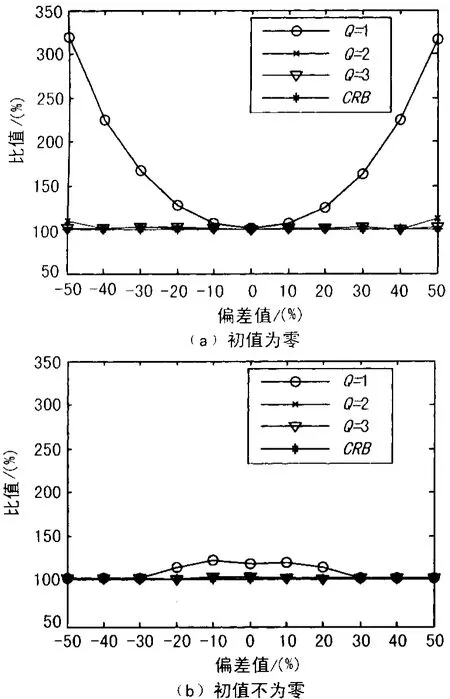
图1 迭代次数与算法收敛性的性能曲线

从图1中可以看到,当频率修正项初值^δ0为零时,算法在第2次测频均方误差已经接近CRB,算法已经收敛;当频率修正项初值^δ0不为零时,算法在第1次测频均方误差就接近CRB,算法收敛。因此设置频率修正项初值后算法可以减少1次迭代。

2.2 测频精度与信噪比

仿真参数设置如下:fs=51.2 MHz,N=512,A=1,fc=12.85 MHz,φ=π/4,SNR取-15 dB～5 dB,步长1 dB,分别做1 000次Monte-Carlo试验。新算法1次迭代(Q=1)与AR建模法[1]和文献[5]中的测频算法的频率估计均方误差(MSE)如图2所示。

由图2可以看到,新算法与AR建模法性能相当,但运算要比后者少;与文献[5]算法相比,新算法在信噪比大于-10 dB后要优于后者。

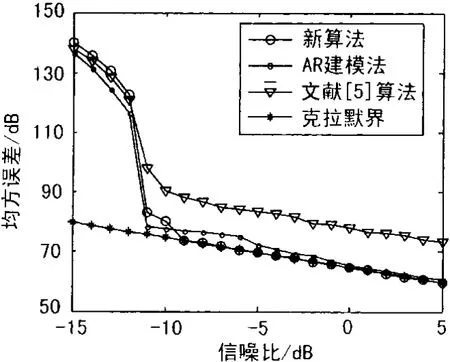
图2 测频精度与信噪比的性能曲线

2.3 测频精度与数据长度

仿真参数设置如下:fs=51.2MHz,A=1,fc=12.85MHz,φ=π/4,SNR=-5 dB,N取 8、16、32、64、128、256、512、1 024,分别做 1 000 次Monte-Carlo 试验。新算法1次迭代(Q=1)与AR建模法和文献[5]中的测频算法的频率估计均方误差(MSE)如图3所示。

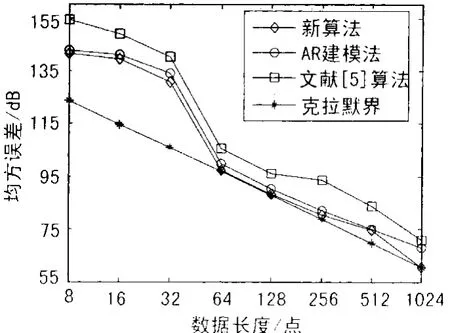
图3 测频精度与数据长度的性能曲线

从图3中可以知道,当数据长度大于32点时,新算法的测频精度已经接近CRB,并且和AR建模法性能相当,但优于文献[5]中的算法。

3 结束语

理论分析和仿真表明,基于DFT系数来构造频率修正项的高精度信号频率估计新算法,能有效减少迭代次数,提高测频精度,具有广泛的适用性,可直接应用于宽带数字接收机的快速高精度频率估计。

[1]TSUI J.Digital Techniques for Wideband Receivers[M].USA:Artech House,2002.

[2]朱小勇,丁 康.离散频谱校正方法的综合比较[J].信号处理,2001,17(l):91-94.

[3]朱雪田,彭玉华.低信噪比下的提高正弦波频率估计精度算法[J].电路与系统学报,2001,6(4):103-106.

[4]AHOUTANIOS E,MULGREW B.Iterative Frequency Estimation by Interpolation on Fourier Coefficients[J].IEEE TransSignal Processing,2005,53(4):1237-1242.

[5]祝 俊,唐 斌,陈 兵.快速高精度实正弦信号频率估计算法[J].电子测量与仪器学报,2008,12(6):65-68.