延迟复杂动态网络的稳定性研究

李涛 于晓楠

1沈阳理工大学 辽宁 110168 2大连海事大学 辽宁 116023

0 引言

目前，复杂网络的整体动力学行为和整个网络的拓扑结构的相互作用的研究引起广泛的关注。研究复杂网络的最终目的是要了解网络的结构如何影响网络的动力学行为，以及反过来网络的结构如何受动力学影响，复杂网络的牵制控制及其稳定性分析就是其中一项重要的研究内容。在控制一个复杂网络达到某一稳定状态时，牵制控制是一种十分经济实用的控制策略。特别是通过对网络中的少数节点施加线性误差反馈控制将网络稳定到一个均匀的平衡点状态，即是网络中的每个节点的状态都稳定到单个节点的平衡点上。一个很有趣的结论就是仅仅控制网络中的任何一个节点，就可以将整个复杂动态网络控制到这样一个均匀的平衡点状态。

1 预备知识

考虑一个由N个相同的线性分散耦合节点构成的延迟复杂动态网络，其中每个节点都是一个n维的动力学系统。第i节点的状态方程为：

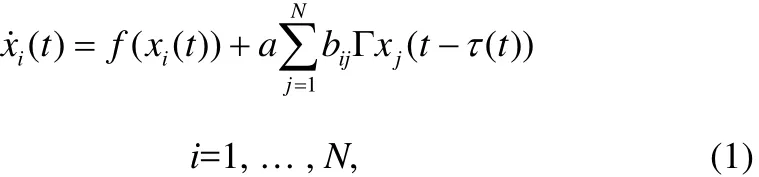
这里x(t) = (x(t),x(t) , L ,x(t) )T∈Rn是第i个节点的状

ii1i2in态向量，常数τ(t)＞0代表延迟函数。f(·)是一个描述节点动力学特性的连续可微的向量函数，常数a＞ 0 是网络的耦合强度。常数对称矩阵 Γ = （γ）∈Rn×n是各个节点状态变量ij之间的内部耦合矩阵，这里假设每个节点的内部耦合矩阵是完全相同的。耦合矩阵B= (bij) ∈RN×N代表网络的拓扑结构，若节点i和j(j≠i)之间有连接，则bij=bji= 1 ；否则bij=bji= 0 。在本文的模型中，耦合系数满足如果节点的度ki定义为与第i个节点连接的边的数目，则

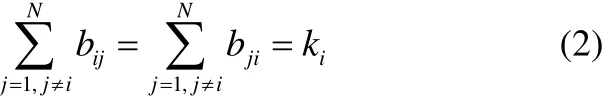
我们的目标是使网络达到一个稳定状态，也就是当t→∞时

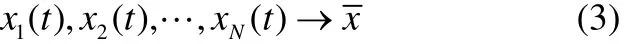
这里是孤立节点的平衡点，满足条件

为了实现目标(4)我们选择控制网络中的部分节点来达到控制整个网络的目的。不失一般性，我们选择前l个节点作为被控节点，l是Nδ的整数部分。

因此，该被控网络的第i个节点的状态方程为：

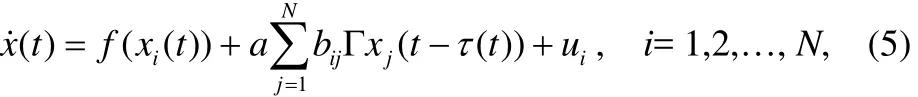
该系统的局部负反馈控制器的方程为：

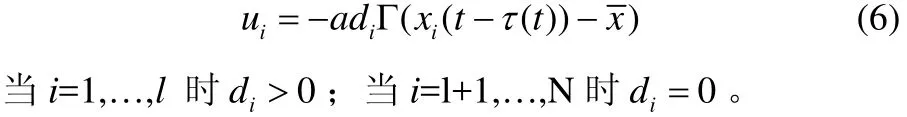
本文考虑的是无向网络，同时我们假设网络(1)是连同的。从而我们得到耦合矩阵B是一个不可约的实对阵矩阵，即T

BB= 。对于本文中其他部分，我们作出如下假设：

假设 1.()tτ是一个可微函数，满足下列条件：

引理1. 如果一个实对称不可约矩阵B= (bij) ∈RN×N满足下列两个条件：

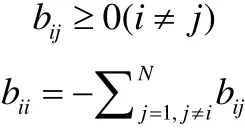
则有：

(a) 0是矩阵 B的最大特征值且对应的特征向量为[1,1, ,1]T

L ；

(b) B的其它特征值都是负实数；

(c) 存在一个非奇异矩阵

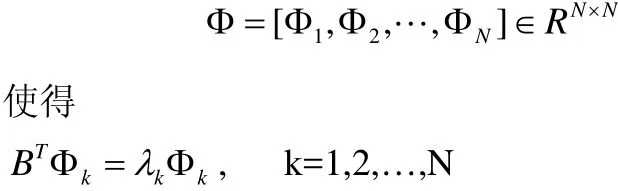
这里 0 =λ1＞λ2≥λ3≥ L ≥λN是矩阵B的特征值。

引理2.如果矩阵B符合引理1中的定义，非零对角矩阵D定义如下：

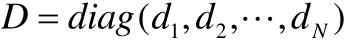
这里di≥ 0 (i= 1 , 2,L ,N)，

则C=B-D是负定矩阵。

引理3.假设

Q(x) =QT(x)、R(x) =RT(x)线性矩阵不等式

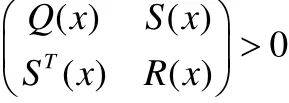
与下面的条件之一等价：

(a)Q(x) ＞ 0 ,R(x) -ST(x)Q-1(x)S(x) ＞ 0

(b)R(x)＞ 0 ,Q(x) -S(x)R-1(x)ST(x) ＞ 0

2 带有时变延迟的复杂动态网络的牵制同步判据

定理1.如果下列N个微分方程

η˙k(t) =J(t)ηk(t) +aλkΓηk(t-τ(t)), i=1, 2, …, N, (8)

关于其零解渐进稳定，则被控网络(5)能够达到局部渐进稳定。

这里J(t) ∈RN×N是f(xi(t))在s(t)附近估计的 Jacobian矩阵。

证明. 定义误差系统ei=xi(t) -x,i=1, 2, …,N，则有

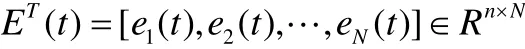
由于f(xi(t))是连续可微的，将被控网络(5)在平衡状态附近线性化，得到；

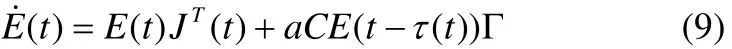
这里J(t) ∈Rn×n是f(xi(t))在x附近估计的 Jacobian矩阵，且C=B-D，D=diag(d1,d2, LdN)。

由引理1和引理2知C是负定对称矩阵，所以可知C的特征值是严格的小于零的，其特征值定义如下：

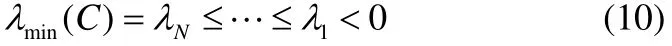
其相对应的特称向量为：

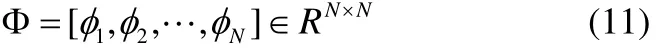
满足：

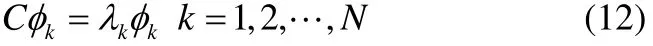
定 义η(t) = (η1(t) ,η2(t) , L ,ηN(t))，基 于 特 征 向 量{φ1,φ2,L ,φN}，我们可以得到：

于是由(9)和(13)可得如下的等式：

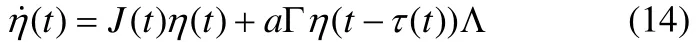
这里 Λ =diag(λ1,λ2,L ,λN)，所以我们只需要使下列N个微分方程：

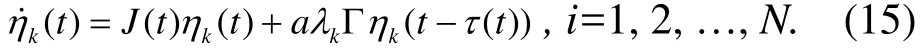
关于其零解渐进稳定，则被控网络(5)能够达到局部渐进稳定，证毕。

最后指出：这里我们将(N×n)维的非线性系统(5)的局部稳定性问题转化为N个独立的m维的线性系统(8)的稳定性问题。

下面的定理给出了复杂网络关于平衡状态x的局部渐进稳定的充分条件。

定理2.如果存在矩阵P＞ 0 ，Q＞ 0 ，R＞ 0 ，M＞ 0 和适当维数的矩阵N1，N2满足下列条件：

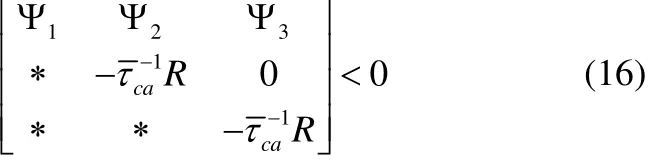
则被控网络(5)能够达到局部渐进稳定。

这里

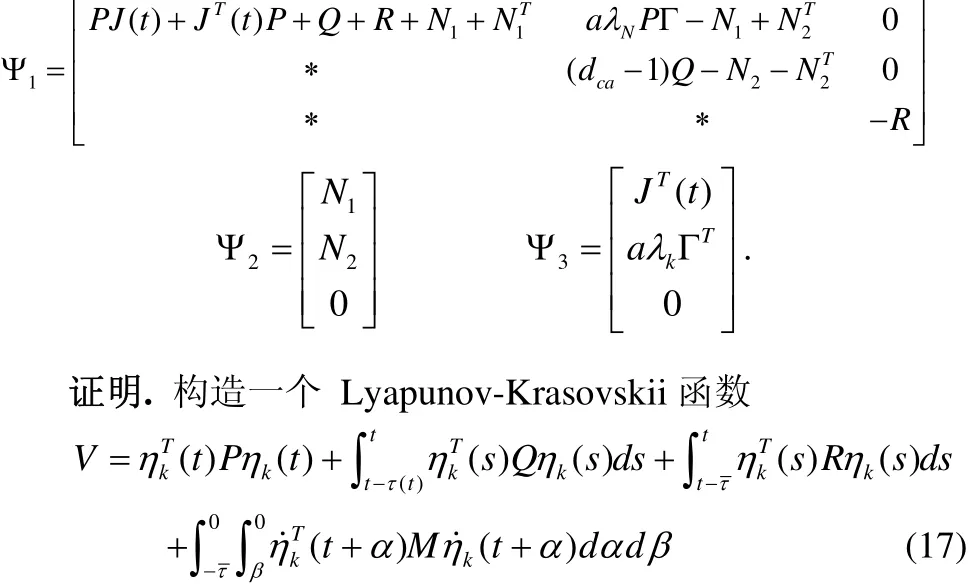
则有：

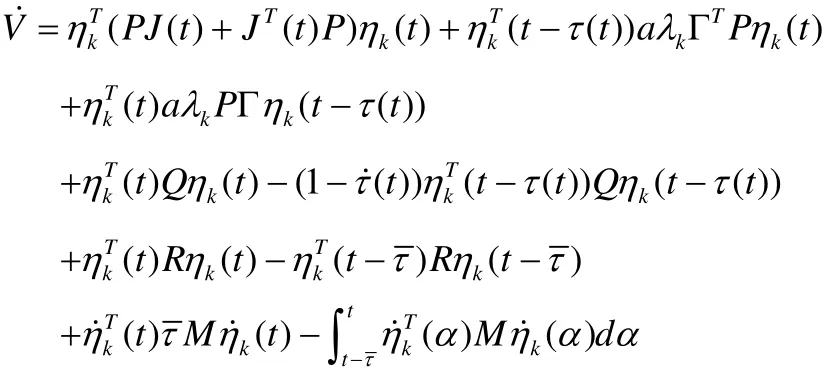
由Newton-Leibniz 公式可得下面的公式：

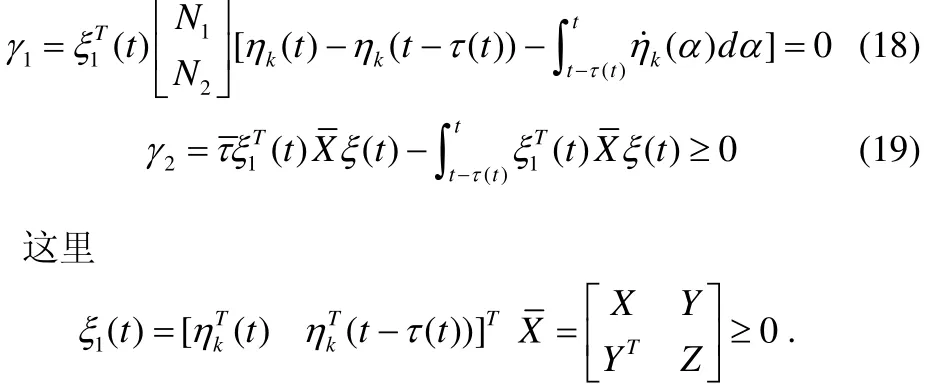
那么下面我们可以得到

则我们可以知系统(8)局部渐进稳定。

由引理3，可知式(23)等价于下式：

通过引理3，由式(22)和(24)我们可以得到以下的稳定性条件：

再由引理3知条件(11)与条件(25)等价，所以0V＜˙，也就是说被控网络(5)能够达到局部渐进稳定。

3 仿真实例

为了验证前面得到的理论结果，下面我们以三维非线性系统为节点构成的网络为例进行分析。这里我们只选择具有代表性的BA无标度网络进行仿真。

我们取平衡状态x= [ 0 0 0]T考虑全状态耦合矩阵Γ=diag(1 1 1)，则整个被控网络可以描述为：

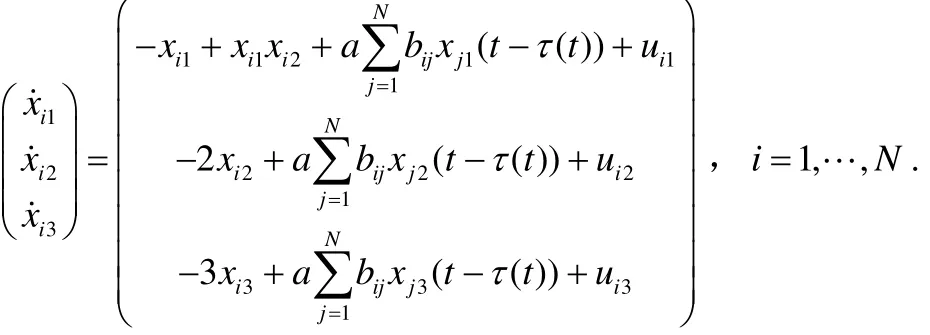
设计如下的状态反馈控制律：

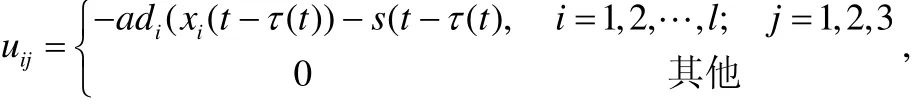
在下面的仿真研究中，考虑耦合时延τ(t)=sin(t)+1选择了网络规模有 50个节点(N=50)，初始值一致分布在区间[-1 1]内的BA无标度网络。根据定理的结论，可求得耦合强度0＜a＜0.08。

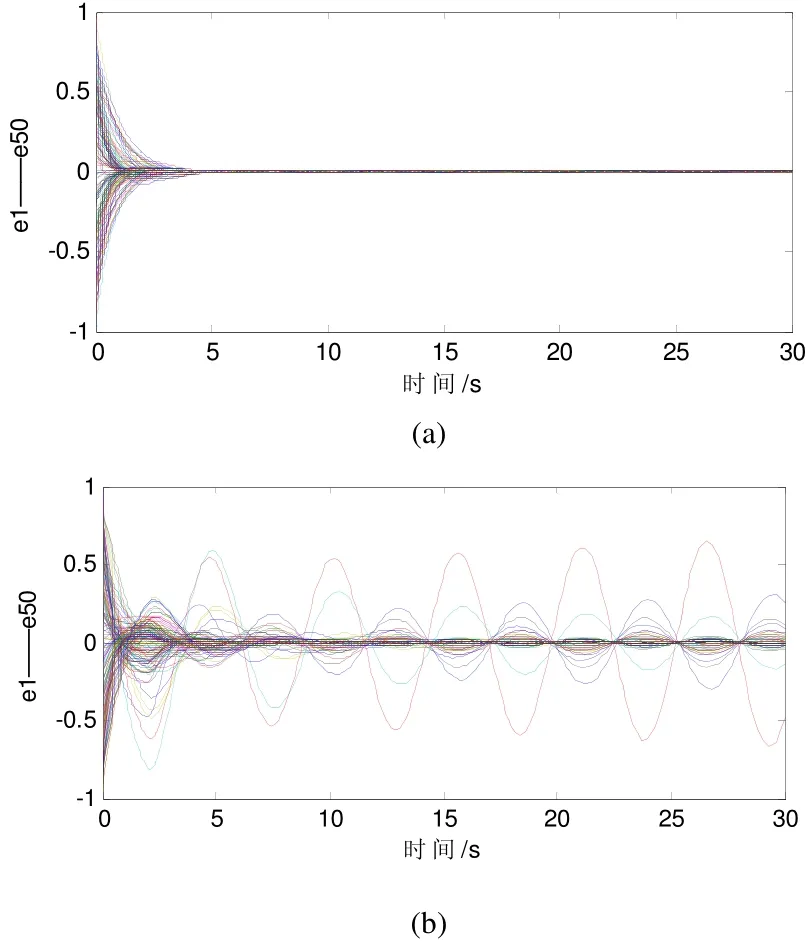
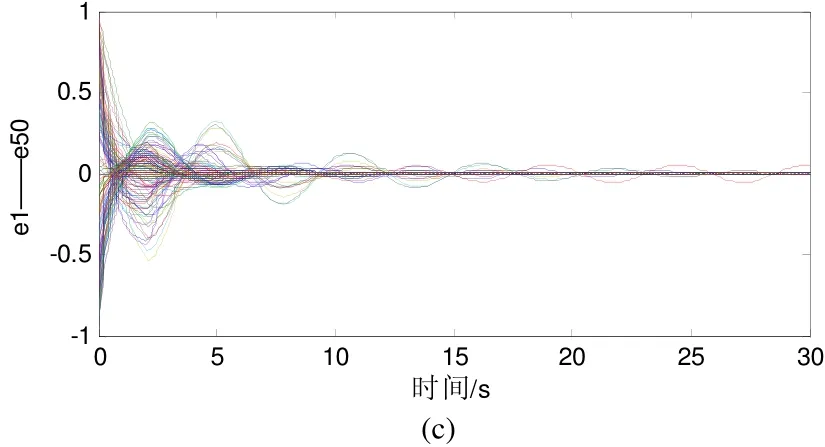
图1 无标度网络在 0.09a= 时的状态变化图

图1(a)和(b)给出了不同的耦合强度对应的网络节点的状态变化图。当 0.02a= 时满足稳定条件，网络能够达到稳定状态；当 0.09a= 时不满足稳定条件，网络不能达到稳定状态。所以说耦合强度过大反而会破坏网络的稳定性；而对于无延迟网络来说，随着耦合强度的增大网络的稳定性能会增强。

图 1(a)是在 0.09a= 时牵制控制度最大的节点时的控制效果图，从图1(b)中可以看出在未施加控制时网络不能达到稳定状态；而在牵制其中一个度最大的节点后，网络能够很快的达到稳定状态。这说明特定牵制控制BA无标度网络的一个节点就能达到很好的控制效果。

4 总结

本文主要研究了带有时变延迟的复杂动态网络的稳定性问题，得到了与时间相关的稳定条件。选择的 Lyapunov-Krasovskii函数能够充利用这个延迟量的信息，降低了所得稳定条件的保守性。所用的方法主要是在平衡点附近进行了线性化处理，同时将网络相互关联的N个动力学系统解耦为N个独立的动力学系统，使得网络复杂的动力学特性变得容易处理。在此基础上，我们对每个独立的系统进行分析，得到确保整个网络达到稳定状态的充分条件。本文的研究还表明：复杂的网络节点的动力学特性、节点之间的耦合强度、内部的耦合矩阵、节点的耦合特征矩阵和牵制反馈增益等共同决定着复杂网络的稳定性能。

[1]D.J. Watts, S.H. Strogatz, Collective dynamics of ‘small world’ networks.1998.

[2]A.-L. Barabási, R. Albert, Emergence of scaling in random networks.1999.

[3]X.F. Wang, G. Chen, Synchronization in scale-free dynamical networks: Robustness and fragility, IEEE Trans. Circuits Syst.2002.

[4]Xiang J, Chen, G R. On the V-stability of complex dynamical net works. Automatica.2007.

[5]Liu Z X, Chen Z Q, Yuan Z Z. Pnning control of weighted general complex dynmical networks with time delay. Physica A.2007.

[6]Zhou J, Lu J, Lü J. Pinning adaptive synchronization of a general complex dynamical network. Automatic.2008.