主动攻击下公钥加密的计算可靠性研究

王文涛

91033部队 山东 266034

0 引言

密码协议分析领域有两类值得注目的方法：符号方法和计算方法。符号方法大都基于DolevYao- 模型，采用模型检测或定理证明。此方法可有效实现自动化，但均假设协议所采用的算法是完美的，攻击者在进行密码分析时得不到任何有用的信息，没有考虑由密码算法以及密码算法与协议交互所产生的安全问题。计算方法假定密码算法是不完美的，攻击者在多项式时间内对协议进行任意攻击，若攻击者能以不可忽略的概率和较少的计算代价伪造协议消息成功，则认为协议是不安全的，这种方法为密码原语和协议提供精确的安全定义，可提供较强的安全保证，但是大都采用手工证明，自动化程度低。

1 计算可靠性论证

1.1 联系N-PAT与IND-CCA

定理 1：如公钥加密方案Aε=(KG,ε,D)是N-PAT安全的，则Aε也是IND-CCA安全的。

证明：假定A为攻击IND-CCA的攻击者，因IND-CCA不允许加密秘密密钥，所以A不能询问加密预言机对 □key,l(term)类型消息的加密，因此不能攻击N-PAT。但因为A对加密预言机的询问为比特串对，而比特串对也可看作模式对，因此可以构建一攻击者B攻击N-PAT，并将A作为B的子程序。假定N-PAT产生n个密钥对(keyi,keyi-1)。

AdvB(η) = P r[(b' =b)]- 1 2，由全概率公式可得到

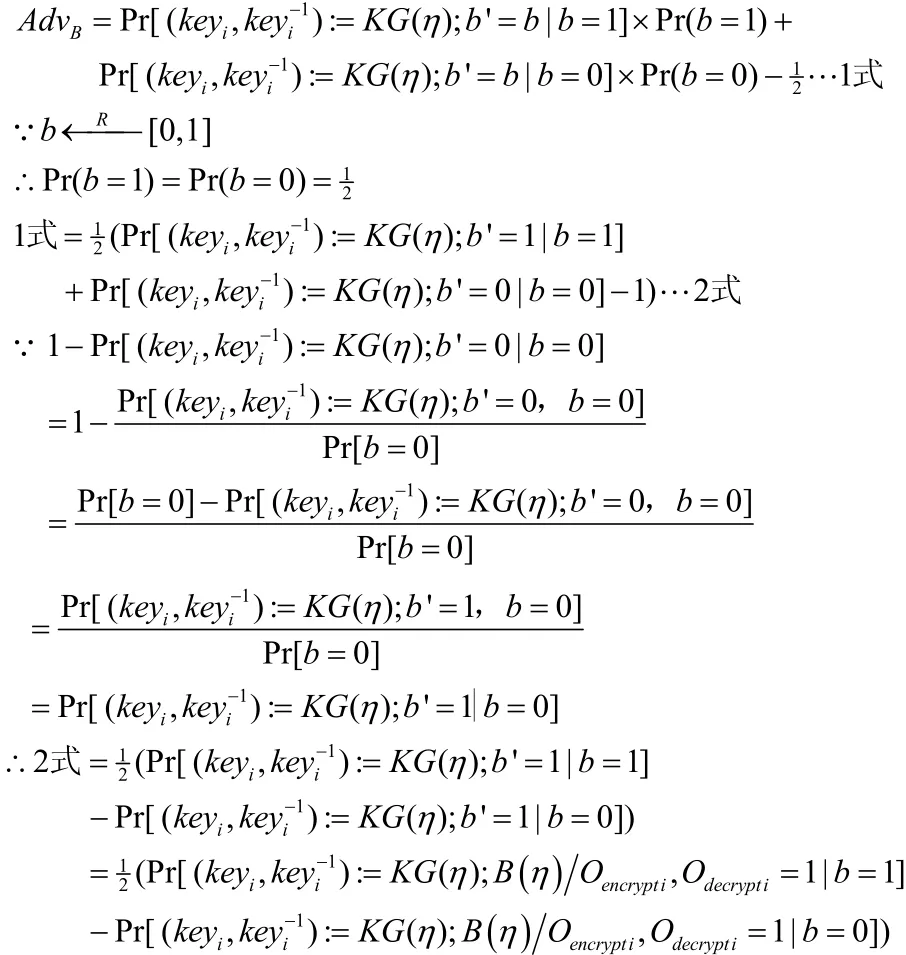
因A是B的子程序，则可用A的执行代替B，且IND-CCA所使用的密钥对属于 (keyi,keyi-1)，预言机属于(Oencrypti,Odecrypti)，我们密钥对为 (key1,key1-1)，预言机为(Oencrypt1,Odecrypt1)。

因Aε是N-PAT安全的，则AdvB(η)≤η，所以AdvA(η)≤η，所以Aε是IND-CCA安全的。

1.2 符号与计算安全性质

协议的认证性与完整性都是迹性质，即可从迹中观察性质是否保持。以认证性“如Bob接受某一密钥K用于与Alice通信，则Alice也参与产生K的协议的相同会话中”为例，对给定的任意迹我们都可看出 Bob是否接受此密钥以及Alice是否参与相同协议的相同会话，因此认证性是迹性质。但秘密性不是基于迹的，如计算不可区分规定计算观察者不可以区分秘密信息传递的情况与非秘密信息传递的情况，但从一个单独的迹上不能看出观察者是否成功区分，这时，需观察在迹上的概率分布，并决定在此分布上的成功概率。

1.2.1 迹性质

此部分借鉴Micciancio-Warinschi方法证明迹性质。

定理2：如公钥加密方案满足N-PAT，则与计算迹相对应的抽象表示的符号迹一定是有效Dolev-Yao迹，即Pr[∃tf∈Execf( ∏ ) |tfExecA,∏(η,R) ]≥1 -f(η)。

证明：每个计算迹Exec(η,R)通过函数c-1:bit→termA,∏建立的映射关系将比特串匹配到消息项，从而确定惟一符号迹tf。下面通过反证法证明tf有效，即如符号攻击者Af执行下的符号迹tf是NDY的，则计算攻击者可攻破Aε。记Af为攻击协议的符号攻击者，Ac是与Af对应的计算攻击者(不攻击密码算法)，我们构建攻击Aε的计算攻击者B，并将Ac作为B的子程序。Af,Ac,B的运行关系如下：如Af发送模式对(pat0,pat1)，相应的，Ac发送的消息为 (pat0,pat1)的计算解释 (c(pat0) ,c(pat1))，通过c:term→bit得到。因Ac为B的子程序，Ac将消息 (c(pat0) ,c(pat1))作为输入给B，B解析(c(pat0) ,c(pat1))，调用加密预言机得到对c(patb) 的加密，最后猜测协议中使用的比特串输出b'∈ [ 0,1]并返回给Ac，相应的，A接收c-1(b')，通过c-1:bit→term得到。如公钥加

f密方案满足N-PAT，则Adv= | Pr[(b' =b) ]-12|≤f(η)，。

如tf是NDY的，则当

(Sidi+1,Si+1,Ei+1)时，。则在mf的解析树中，至少存在一条路径，其叶子节点m|p不是Ei的子项，因为如所有叶子者在Ei中，就与矛盾，又因叶子节点为原子消息(主体标识符、密钥、随机数)，且m|p∉Ei，则m|p不属于主体标识符、不属于公钥、不属于攻击者A产生的随机数、也不属于A所拥有的私钥，因此m|p只能为诚实主体的私钥或诚实主体的随机数。如m|p为诚实主体的随机数(或私钥)，如m|p的父节点是串接，则攻击者都可提取该随机数(或私钥)，即Ei|-mp，这与m|p∉Ei相矛盾；如m|p的父节点存在一个为公钥加密{t}key，其中m|p为t的子项，因，则t和m|p都是秘密的。由此可见，如，则存在加密子模式 □key={t}key∈m且。因攻击者Af发送消息mf，这意味着者Af可从它不能解密的密文□key中提取出诚实主体的私钥或诚实主体的随机数，那么B可推导出c(□key)，与N-PAT相矛盾，则tf有效。

由此我们知道通过双射函数c:term→bit，符号迹与计算迹可以互相转化，如公钥加密方案Aε满足N-PAT，计算攻击者的能力与符号攻击者的能力相同。

记Pf为符号模型中的迹安全性质，由符号迹集合给定，如所有有效迹满足Pf，即Execf(∏)∈pf，则∏|=fPf。如密码协议运行进入某一状态(Sidi,Si,Ki) ，该状态下违背了密码协议的某些预期的安全特性，此时便认为发生了针对密码协议的攻击。Pc为计算模型中相应的迹安全性质，由计算迹集合给定，如所有有效迹满足Pc的概率是不可忽略的，即对任意概率多项式时间下的攻击者Ac而言，P r[ExecA,∏(η,R)∉Pc]≤η，则∏|=cPc。

定义 1[可信抽象]：如(∀tf∈Execf(∏),∀tc∈ExecA,∏(η,R))

(tftc,tf∈pf) → P r [tc∉Pc] ≤η，则称Pf是Pc的可信抽象，记为concr(pf)⊆pc。

定理3：如Pf是Pc的可信抽象，且Aε满足N-PAT，则 ∏ |=fPf→∏|=cPc。即如加密方案满足N-PAT，且符号模型中某命题成立，则在计算模型中该命题也成立。

证明：由定理2可知，对任一计算迹tc∈ExecA,∏(η,R)，都存在一符号迹tf∈Execf( ∏ ),tf∈Pf使得tf≺tc，又因为∏|=fPf，则tf∈pf，由定义1可知 ∀tc∈ExecA,∏(η,R)(tc∈pc)，即∏|=cPc。形式化表示如下：则|ccP∏=。

1.2.2 秘密性

在符号模型中，秘密性可以描述为迹性质，如某消息不能由攻击者推导出来，则称该消息是秘密的。在计算模型中，只有当某消息的任意部分都不能由攻击者推导出来，才称该消息是秘密的。

借鉴Véronique Cortier对协议秘密性的定义，将协议秘密性描述为随机数的秘密性，并证明随机数秘密性的可靠性。在符号模型中，对任一有效符号迹 (Sid0,S0,E0)…(Sidn,Sn,En)，如攻击者都不能推导出随机数n，则此随机数是秘密的。在计算模型中，随机数nc的秘密性描述如下：N-PAT博弈产生两个随机数n0、n1(与pat0、pat1类似)。攻击者目的是猜测nb,b∈ { 0,1}，如攻击者猜测成功的概率可忽略，则称nc是秘密的。

定理4：记N为协议∏的随机数。如公钥加密方案Aε满足N-PAT，且在符号模型中N是秘密的，则在计算模型中与N对应的随机数Nc也是秘密的。

证明：与定理2类似，构建攻击者Af,Ac,B，如Af发送包含N的模式对 (pat0,pat1)，其中，在pat0中N为N0，在pat1中N为N1，则Ac发送的消息为 (pat0,pat1)的计算解释(c(pat0) ,c(pat1))，其中，在c(pat0)中与N对应的随机数Nc为Nc0，在c(pat1)中Nc为Nc1。因公钥加密方案Aε满足N-PAT，则pat0,pat1不可区分。则根据定理2，符号攻击者的攻击能力与计算攻击者的能力相同，所以

因为在符号模型中N是秘密的，即，又因为由定理 2中的证明过程可知，存在加密子项如在计算模型中Nc不是秘密的，即Ac|-Nc，则相对应的，攻击者Af可从它不能解密的密文{t}key中提取出诚实主体的随机数，产生NDY迹，由推论的逆否命题得到公钥加密方案Aε不满足N-PAT，B可攻破Aε，这与前提加密方案满足N-PAT相矛盾。

2 结束语

原始Micciancio-Warinschi方法不能分析包含类型消息的协议，这限制了它的应用领域。本文对Micciancio-Warinschi方法进行了扩展，并证明了在公钥加密方案满足安全定义N-PAT时，符号形式化系统所得结论在计算模型中也成立。基于该结论，可以构建或改进符号形式化分析系统，使其具有计算可靠性。下一步，我们将在符号模型下考虑密码算法的影响，实现密码协议的安全性验证。

[1]ABADI M,ROGAWAY P.Reconciling two views of cryptography(The computational soundness of formal encryption)[C].In Proc.1st IFIP International Conference on Theoretical Computer Science.Springer.2000.volume 1872 of LNCS 3-22.

[2]ABADI M,JURJENS J.Formal eavesdropping and its computational interpretation[C].In Proc.4th International Symposium on Theoretical Aspects of Computer Software (TACS). 2001.

[3]MICCIANCIO D,WARINSCHI B.Completeness theorems for the Abadi-Rogaway logic of encrypted expressions[J].Journal of Computer Security.2004.